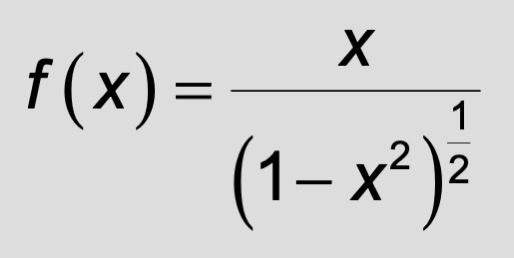Ableitung Von Brüchen Mit X Im Nenner
Okay, Leute, setzt euch bequem hin, bestellt euch 'nen Kaffee (oder was Härteres, je nachdem wie eure Mathe-Angst ausgeprägt ist), denn wir tauchen heute ein in die wunderbare, manchmal leicht verrückte Welt der Ableitung von Brüchen, wo das X im Nenner sein Unwesen treibt. Keine Panik, ich verspreche euch, am Ende werdet ihr das Ding beherrschen wie 'nen Jongleur, der gleichzeitig mit brennenden Fackeln und rohen Eiern hantiert! (Okay, vielleicht nicht ganz *so* beeindruckend, aber ihr versteht den Punkt.)
Das Problem: X ist im Keller!
Stellt euch vor, ihr habt einen Kuchen (immer gut, mit Kuchen anzufangen, oder?), und der Kuchen wird durch *x* geteilt. Also, nicht in Stücke geschnitten, sondern... nun ja, durch *x* geteilt. Das Ergebnis ist eure Funktion. Mathematisch sieht das dann so aus: f(x) = irgendwas / x. Das "irgendwas" kann auch noch komplizierter sein, aber fürs Erste tun wir mal so, als wäre es eine einfache Zahl, sagen wir mal 5. Also, f(x) = 5/x.
Das Problem ist, dass dieser *x* da unten im Nenner sitzt und uns das Leben schwer macht. Es ist wie mit dem Mitbewohner, der nie den Müll rausbringt. Man muss ihn irgendwie *bearbeiten*. Aber keine Sorge, wir haben die Werkzeuge!
Die Lösung: Quotientenregel – Der Superheld der Brüche
Hier kommt unser Superheld ins Spiel: die Quotientenregel! Sie ist wie Batman für Brüche, immer zur Stelle, wenn’s brenzlig wird. Sie sagt im Wesentlichen (und jetzt haltet euch fest, es wird kurz technisch):
Wenn f(x) = u(x) / v(x), dann ist f'(x) = (u'(x) * v(x) - u(x) * v'(x)) / (v(x))^2.
Puh, das klingt nach mehr Mathe, als man nach dem zweiten Kaffee vertragen kann, aber keine Sorge, wir brechen es runter. u(x) ist der Zähler (der Kuchen selbst), und v(x) ist der Nenner (der Mitbewohner, der den Kuchen teilt). Die Ableitungen davon sind u'(x) und v'(x). Denkt dran: Ableiten heißt, die Steigung zu finden! Wie steil ist der Kuchenkonsum, wenn x sich ändert?
Ein Beispiel für Dummies (wie mich, wenn es um komplexe Zahlen geht)
Nehmen wir unser Beispiel von vorhin: f(x) = 5/x. Hier ist u(x) = 5 und v(x) = x.
Die Ableitung von u(x) = 5 ist u'(x) = 0 (denn 5 ist eine Konstante, und Konstanten haben keine Steigung, sie sind einfach... da). Die Ableitung von v(x) = x ist v'(x) = 1 (denn die Steigung einer geraden Linie mit der Gleichung y = x ist 1).
Jetzt setzen wir alles in unsere Superhelden-Formel ein:
f'(x) = (0 * x - 5 * 1) / (x)^2 = -5 / x^2.
Tada! Wir haben die Ableitung! Das bedeutet, dass die Steigung der Funktion f(x) = 5/x an jedem Punkt x durch -5/x^2 gegeben ist. Und glaubt mir, wenn ihr das versteht, könnt ihr eure Freunde auf der nächsten Party beeindrucken. (Oder zumindest verwirren.)
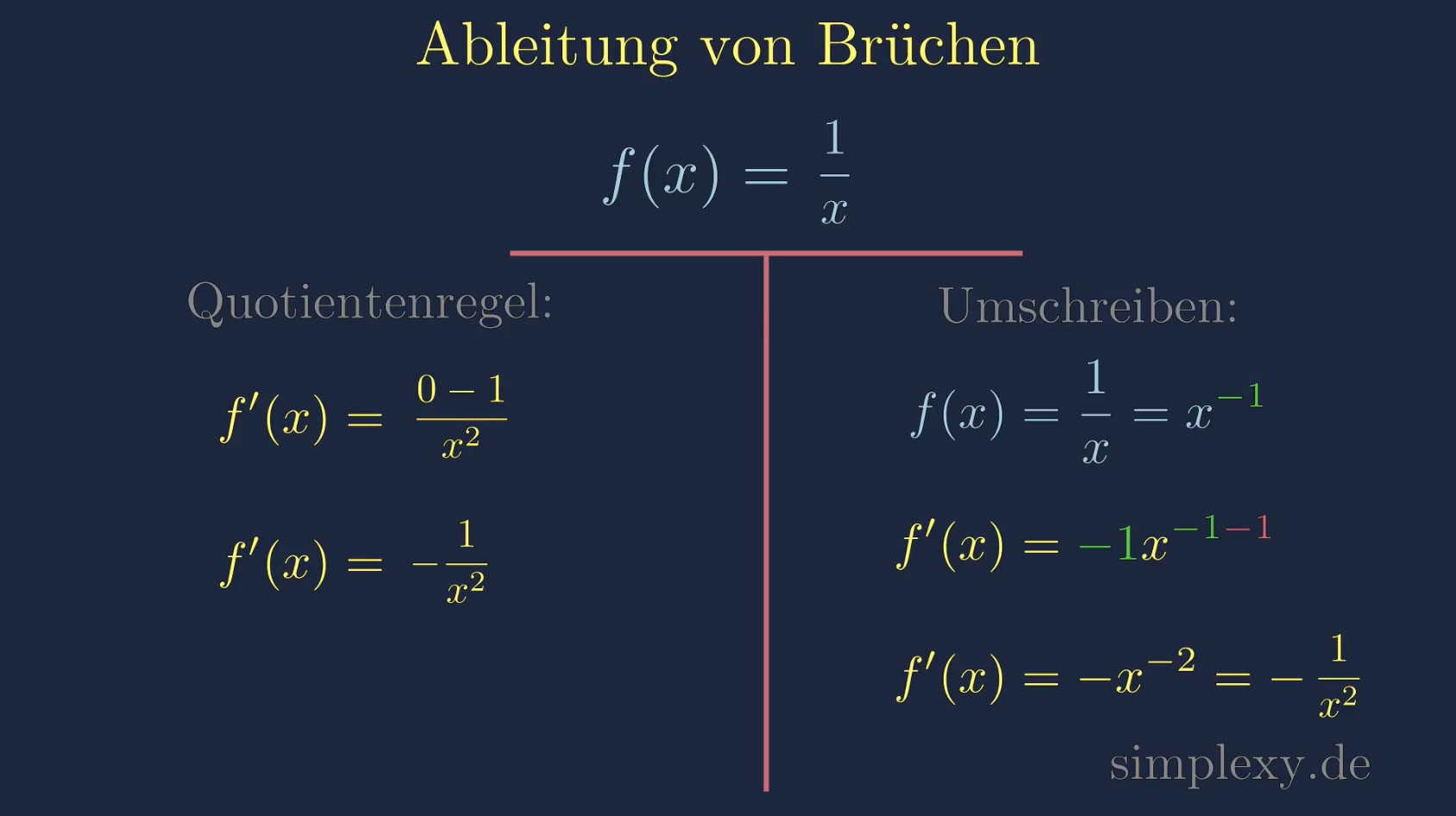
Spezialfall: 1/x – Der Rockstar unter den Brüchen
Der Bruch 1/x ist so wichtig, dass er seinen eigenen Song verdient hätte. Seine Ableitung ist -1/x^2. Merkt euch das! Es ist wie die Hauptstadt von Frankreich – einfach wichtig zu wissen.
Wenn's komplizierter wird: Die Kettenregel hilft!
Was, wenn unser Nenner nicht einfach nur *x* ist, sondern irgendwas Verrücktes, wie (x^2 + 3x – 1)? Kein Problem, dafür haben wir die Kettenregel! Sie ist wie ein Schweizer Taschenmesser für Ableitungen. Im Grunde kombiniert sie die Quotientenregel mit der Ableitung der inneren Funktion des Nenners. Das ist ein bisschen viel auf einmal, aber das Prinzip ist: Ableiten von außen nach innen!
Die Moral von der Geschicht': Übung macht den Meister!
Das Ableiten von Brüchen mit *x* im Nenner kann anfangs einschüchternd sein, aber mit ein bisschen Übung wird es zur Routine. Denkt dran: Die Quotientenregel ist euer Freund, und die Kettenregel euer Schweizer Taschenmesser. Und wenn alles schiefgeht, esst ein Stück Kuchen. Das hilft immer. (Vielleicht nicht bei Mathe, aber beim allgemeinen Wohlbefinden definitiv.)
Also, geht raus und leitet fleißig ab! Und wenn ihr Fragen habt, fragt einfach. Es gibt keine dummen Fragen, nur dumme Ableitungen... äh, Quatsch. Bis zum nächsten Mal!