Abstand Eines Punktes Von Einer Geraden Berechnen

Ein Punkt, eine Linie und die Frage aller Fragen: Wie weit weg bist du?

Stell dir vor, du bist auf einer Party. Eine lange Schlange vor dem Buffet (das ist unsere Linie) und du, mit deinem Teller, stehst irgendwo im Raum (unser Punkt). Die brennende Frage: Wie nah bin ich am Essen? Das ist im Grunde das Problem, das wir heute lösen wollen: Den Abstand eines Punktes von einer Geraden berechnen. Aber keine Sorge, es wird weniger mathematisch als es klingt, versprochen!

Vergiss für einen Moment komplizierte Formeln und Koordinatensysteme. Denk stattdessen an eine romantische Komödie. Der Punkt, das bist du, sehnsüchtig auf der Suche nach der Linie (deinem Traumpartner/deiner Traumpartnerin). Die Linie, nun ja, die ist da, wunderschön und unerreichbar – zumindest fühlt es sich so an. Der Abstand? Das ist die Herausforderung, die es zu überwinden gilt, die Entfernung, die zwischen euch steht.

Warum ist das überhaupt wichtig? Abgesehen von der Buffet-Analogie und der romantischen Sehnsucht? Nun, stell dir vor, du bist ein Architekt. Du planst ein Haus und musst sicherstellen, dass die Fundamente (Punkte) den richtigen Abstand zu den Stromleitungen (Linien) haben. Oder ein Landwirt, der seine Felder so anordnen muss, dass sie nicht von einem Fluss (der Linie) überschwemmt werden. Oder, ganz trivial, du willst einfach nur dein Bild gerade an der Wand aufhängen und nutzt dafür eine Wasserwaage (die Linie) und einen Punkt an der Wand (der Punkt). Es gibt überall Linien und Punkte!

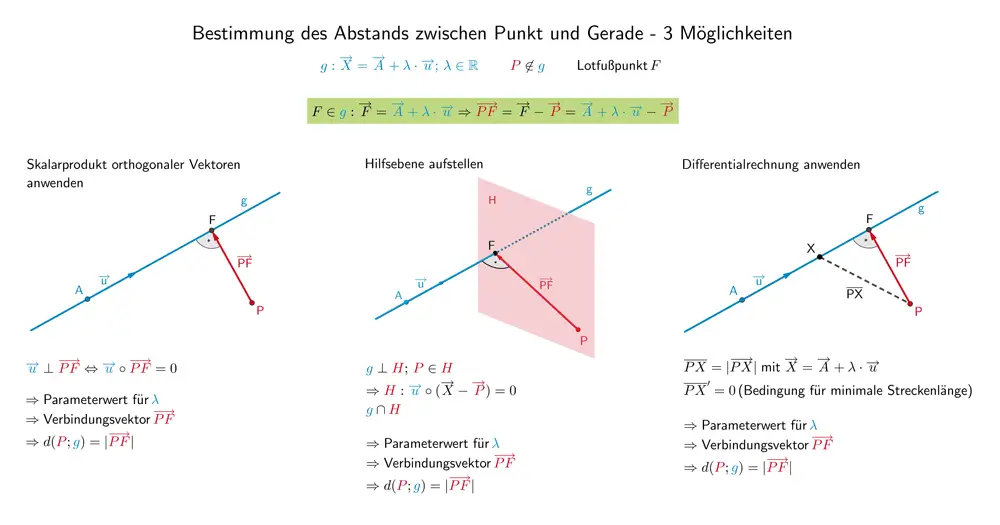
Okay, ein bisschen Mathematik muss sein, aber keine Angst, wir machen es ganz sanft. Stell dir vor, du wirfst einen Stein auf die Linie. Aber nicht einfach so! Du wirfst ihn so, dass er senkrecht auf die Linie trifft. Dieser senkrechte Weg ist der kürzeste Weg – und das ist genau der Abstand, den wir suchen. Stell dir vor, du würdest ein Seil von deinem Punkt zur Linie spannen. Das kürzeste, straffste Seil, das ist der Abstand. Klingt doch gar nicht so schlimm, oder?

Die heimliche Heldin: Die Formel (Pssst!)

Ja, es gibt eine Formel. Aber wir behandeln sie wie eine geheime Zutat in Omas Kuchenrezept. Wir flüstern sie uns zu, benutzen sie, und vergessen sie dann schnell wieder. Die Formel, in aller Kürze (und ohne jegliche Erklärung, weil es ja "einfach und lustig" bleiben soll):

|Ax₁ + By₁ + C| / √(A² + B²)

Klingt furchteinflößend? Ist es nicht! Denk einfach an ein paar Buchstaben und Zahlen, die zusammenarbeiten, um das Problem zu lösen. A, B und C kommen von der Geradengleichung (die wir geflissentlich ignorieren), und x₁ und y₁ sind die Koordinaten unseres Punktes. Alles klar? Gut! Verwirrt? Auch gut! Hauptsache, du hast Spaß dabei!

Das Schöne an der Mathematik ist ja, dass sie manchmal überraschend alltagstauglich ist. Wer hätte gedacht, dass man mit einer Formel, die aussieht wie ein außerirdischer Code, den Abstand zum Buffet, zum Traumpartner oder zur Stromleitung berechnen kann?

Und jetzt kommt der Clou: Es gibt online unzählige Rechner, die dir die ganze Arbeit abnehmen. Du gibst einfach die Koordinaten des Punktes und die Geradengleichung ein, und *schwupps*, da ist der Abstand. Also, wenn du das nächste Mal vor einem kniffligen Problem stehst, denk daran: Es gibt wahrscheinlich eine Formel (oder einen Online-Rechner) dafür. Und selbst wenn nicht, ist es immer gut zu wissen, dass es da draußen eine Welt voller Punkte, Linien und Abstände gibt, die darauf warten, entdeckt zu werden.

Vergiss also nicht, die nächste Party ist die perfekte Gelegenheit, dein neu erworbenes Wissen anzuwenden. Beobachte die Warteschlange am Buffet (die Gerade) und dich selbst (den Punkt). Berechne deinen inneren Abstand und stürze dich ins Getümmel! Viel Erfolg!