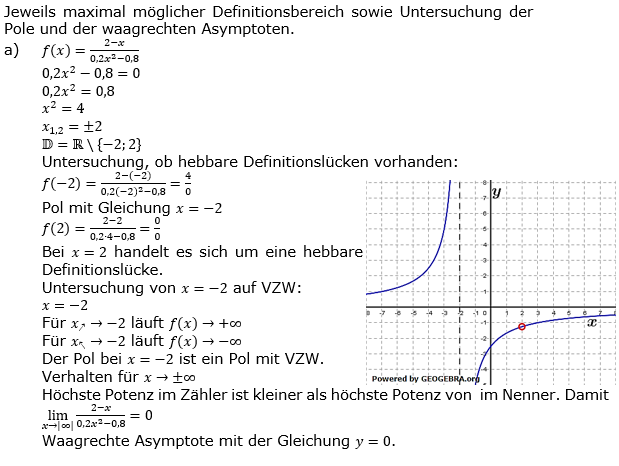
Aufgaben Gebrochen Rationale Funktionen
Hey du! Hast du jemals das Gefühl gehabt, Mathematik sei wie ein gruseliger Wald voller unbekannter Kreaturen? Keine Sorge, das geht vielen so! Aber heute nehmen wir uns einen ganz besonderen Baum im Wald vor: die gebrochen rationalen Funktionen. Klingt erstmal kompliziert, oder? Aber glaub mir, das wird spaßiger als du denkst! (Und nein, ich verspreche dir keine Einhörner, aber vielleicht ein Aha-Erlebnis oder zwei.)
Was sind denn diese geheimnisvollen Funktionen überhaupt? Stell dir vor, du hast einen Kuchen. (Wer liebt keinen Kuchen?) Eine gebrochen rationale Funktion ist im Grunde ein Bruch, bei dem sowohl im Zähler als auch im Nenner Polynome stehen. Polynome, das sind diese Ausdrücke mit x, x², x³ und so weiter. Also zum Beispiel sowas wie (x + 2) / (x² - 1). Siehst du? Ein Bruch! Mit Polynomen! Easy peasy lemon squeezy, wie man so schön sagt!
Warum sollten wir uns überhaupt damit beschäftigen? Gute Frage! (Ich liebe gute Fragen!) Gebrochen rationale Funktionen sind überall um uns herum! Sie beschreiben viele reale Phänomene. Denk zum Beispiel an die Ausbreitung von Krankheiten, die Konzentration von Medikamenten im Blutkreislauf oder sogar die Gestaltung von Achterbahnen! (Okay, vielleicht nicht *direkt* die Achterbahnen, aber die mathematischen Prinzipien dahinter sind verwandt!)
Die Aufgaben: Was erwartet dich?
Okay, genug Theorie. Lass uns mal über die Aufgaben sprechen. Was wird von dir erwartet, wenn du dich mit gebrochen rationalen Funktionen beschäftigst? Hier sind ein paar der häufigsten Herausforderungen (die wir aber zusammen meistern werden!):
- Definitionsbereich bestimmen: Wo darf unser "x" denn überall rein? Gibt es Werte, die den Nenner Null machen? (Spoiler Alert: Die sind tabu! Division durch Null ist ein No-Go!)
- Nullstellen finden: Wo schneidet die Funktion die x-Achse? Das sind die Stellen, an denen der Zähler Null wird.
- Polstellen analysieren: Was passiert, wenn wir uns einer Stelle nähern, die den Nenner Null macht? Die Funktion rast entweder ins Unendliche oder ins Minus-Unendliche. Das sind die berüchtigten Polstellen!
- Asymptoten bestimmen: Wie verhält sich die Funktion für sehr große oder sehr kleine Werte von "x"? Gibt es Geraden, denen sich die Funktion annähert?
- Funktionsgraphen skizzieren: Das ist die Königsdisziplin! Wenn du alle oben genannten Punkte kennst, kannst du den Graphen der Funktion zeichnen und dir ein Bild davon machen, wie sie aussieht.
Klingt nach viel? Ja, vielleicht. Aber keine Panik! Jede dieser Aufgaben ist wie ein kleines Puzzle. Und wenn du die einzelnen Puzzleteile zusammensetzt, ergibt sich ein wunderschönes Bild – der Funktionsgraph!
Warum das Ganze Spaß machen kann (ja, wirklich!)
Du fragst dich jetzt vielleicht: "Mathe und Spaß? Geht das überhaupt zusammen?" Absolut! Wenn du erstmal verstanden hast, wie gebrochen rationale Funktionen funktionieren, wirst du feststellen, dass sie ein mächtiges Werkzeug sind, um die Welt um dich herum zu verstehen. Es ist wie ein neues Paar Augen, mit dem du Muster und Zusammenhänge erkennen kannst, die du vorher nicht gesehen hast.
Außerdem ist es einfach cool, wenn du eine Aufgabe löst, die am Anfang unlösbar schien! Dieses Gefühl, wenn du endlich den Dreh raus hast und alles zusammenpasst – unbezahlbar! Und mal ehrlich, wer kann schon von sich behaupten, dass er/sie gebrochen rationale Funktionen versteht? Du bald, mein Freund/meine Freundin!
Mach den ersten Schritt!
Also, bist du bereit, dich auf dieses Abenteuer einzulassen? Fang klein an. Such dir ein paar einfache Beispiele und versuche, die einzelnen Schritte zu verstehen. Frag deine Lehrer, deine Freunde oder schau dir Online-Tutorials an. Es gibt unzählige Ressourcen, die dir helfen können. Glaube an dich selbst! Du kannst das schaffen! Und wer weiß, vielleicht entdeckst du ja sogar deine Leidenschaft für die Mathematik! (Okay, vielleicht nicht *Leidenschaft*, aber zumindest ein bisschen Respekt und Anerkennung für ihre Schönheit und Nützlichkeit.)
Denk daran: Jede Reise beginnt mit einem ersten Schritt. Mach ihn jetzt! Und wer weiß, wohin er dich führt! Vielleicht wirst du eines Tages sogar eine Achterbahn entwerfen… oder zumindest verstehen, wie sie funktioniert! Die Welt der gebrochen rationalen Funktionen wartet auf dich! Und sie ist gar nicht so gruselig, wie sie am Anfang aussieht. Versprochen!