Aufgaben Proportionale Und Antiproportionale Zuordnungen

Hey Leute! Habt ihr euch jemals gefragt, warum die riesige Pizza so viel mehr kostet als die kleine? Oder warum ihr länger braucht, um eine lange Strecke zu fahren als eine kurze? Dann seid ihr hier genau richtig! Heute tauchen wir ein in die Welt der proportionalen und antiproportionalen Zuordnungen. Keine Panik, das klingt komplizierter als es ist! Versprochen!
Was ist das überhaupt?
Stellt euch vor, ihr backt eure Lieblingskekse. Das Rezept sagt: Für 10 Kekse braucht ihr 2 Eier. Wenn ihr 20 Kekse backen wollt, braucht ihr logischerweise 4 Eier. Das ist eine proportionale Zuordnung! Mehr Kekse, mehr Eier. Die Menge der Eier steigt proportional zur Menge der Kekse.
Anders sieht es aus, wenn ihr euch vornehmt, eure Wohnung zu putzen. Sagen wir, ihr braucht alleine 3 Stunden dafür. Wenn ihr aber euren Freund oder eure Freundin dazu überreden könnt, mitzuhelfen, seid ihr vielleicht schon in 1,5 Stunden fertig. Das ist eine antiproportionale Zuordnung! Mehr Helfer, weniger Zeit. Die Zeit sinkt antiproportional zur Anzahl der Helfer.
Proportional: Mehr vom Guten, weniger vom Schlechten!
Denkt an eure Lieblingsmusik. Wenn ihr ein Lied doppelt so oft hört, gefällt es euch wahrscheinlich auch doppelt so gut (okay, vielleicht nicht *doppelt* so gut, aber ihr versteht, was ich meine!). Oder denkt an eure monatliche Handyrechnung. Je mehr Daten ihr verbraucht, desto höher die Rechnung. Das sind alles Beispiele für proportionale Zusammenhänge.
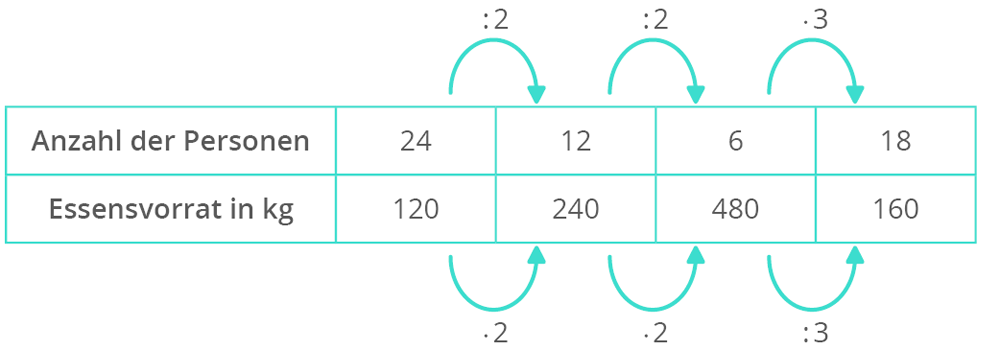
Merke: Wenn das eine steigt, steigt auch das andere (oder wenn das eine sinkt, sinkt auch das andere!). Das Verhältnis bleibt gleich. Stellt euch vor, ihr kauft Äpfel auf dem Markt. 1 Kilo kostet 2 Euro. Dann kosten 2 Kilo 4 Euro, 3 Kilo 6 Euro usw. Das Verhältnis (Euro pro Kilo) bleibt immer gleich: 2 Euro/Kilo.
Eine kleine Anekdote: Als ich klein war, hat meine Oma immer gesagt: "Je mehr du lernst, desto schlauer wirst du!" Recht hatte sie! Das ist auch eine schöne (wenn auch vereinfachte) proportionale Zuordnung.
Antiproportional: Je mehr, desto weniger (oder umgekehrt)!
Stellt euch vor, ihr organisiert eine Party. Je mehr Leute ihr einladet, desto weniger Kuchen bleibt für jeden einzelnen übrig. (Außer natürlich, ihr backt einen riesigen Kuchen!). Oder denkt an ein Auto. Je schneller ihr fahrt, desto weniger Zeit braucht ihr für eine bestimmte Strecke. Das sind antiproportionale Zuordnungen.
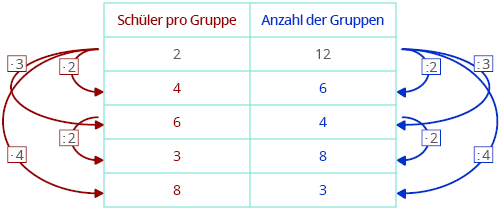
Merke: Wenn das eine steigt, sinkt das andere (oder wenn das eine sinkt, steigt das andere!). Das Produkt bleibt gleich. Denkt an ein Rechteck mit einer Fläche von 24 cm². Wenn die Länge 6 cm beträgt, ist die Breite 4 cm. Wenn die Länge 8 cm beträgt, ist die Breite 3 cm. Die Fläche (Länge x Breite) bleibt immer gleich: 24 cm².
Ein kleines Beispiel aus dem Alltag: Ich habe mal versucht, einen Marathon zu laufen (okay, ich bin nicht wirklich weit gekommen!). Mir wurde schnell klar: Je schneller ich laufe, desto schneller bin ich erschöpft. Eine klassische antiproportionale Zuordnung zwischen Geschwindigkeit und Ausdauer.
Warum sollte mich das interessieren?
Ganz einfach: Proportionale und antiproportionale Zuordnungen helfen uns, die Welt um uns herum besser zu verstehen und Entscheidungen zu treffen. Sie stecken überall drin – beim Kochen, beim Einkaufen, beim Planen von Reisen, sogar beim Spielen von Videospielen! Wenn ihr die Prinzipien versteht, könnt ihr zum Beispiel:
- Besser einschätzen, wie viel Zutaten ihr für ein Rezept braucht.
- Den besten Deal beim Einkaufen finden.
- Eure Reisezeit realistischer planen.
- Verstehen, wie sich die Anzahl der Arbeiter auf die Bauzeit eines Hauses auswirkt.
Und das Beste daran? Es ist gar nicht so schwer, wie es am Anfang klingt. Mit ein bisschen Übung werdet ihr bald zum Meister der Zuordnungen!
Fazit: Es ist alles eine Frage des Verhältnisses!
Ob proportional oder antiproportional, es geht immer darum, das Verhältnis zwischen zwei Dingen zu verstehen. Wenn ihr das einmal verinnerlicht habt, werdet ihr die Welt mit anderen Augen sehen. Und wer weiß, vielleicht spart ihr sogar Geld, indem ihr bessere Entscheidungen trefft!
Also, das nächste Mal, wenn ihr etwas kauft, kocht oder plant, denkt an proportionale und antiproportionale Zuordnungen. Es könnte sich lohnen! Viel Spaß beim Entdecken!