Aufgaben Quadratische Funktionen Mit Lösungen

Quadratische Funktionen. Klingt nach Mathe-Trauma aus der Schulzeit? Keine Sorge, wir verwandeln das Ganze in eine entspannte Angelegenheit. Denk' an sie weniger als komplizierte Gleichungen und mehr als Werkzeuge, um die Welt um dich herum zu verstehen – von Flugbahnen beim Basketball bis hin zu Brückenbögen.

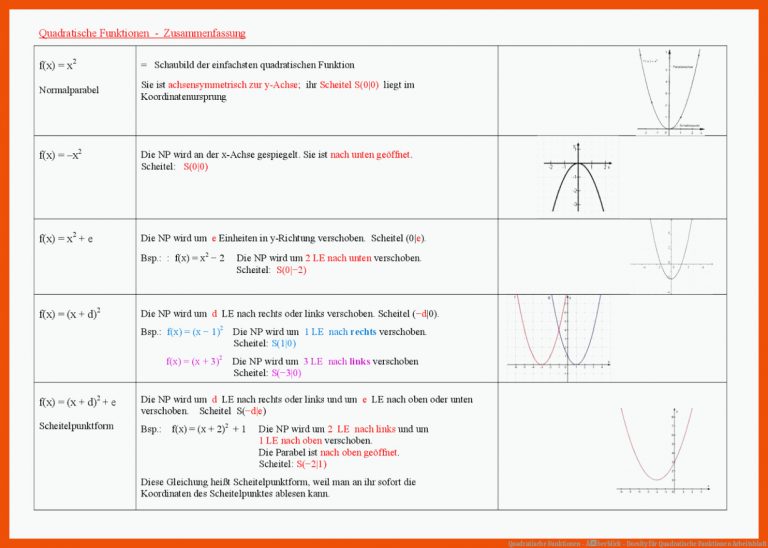
Was sind quadratische Funktionen überhaupt?

Im Kern beschreiben quadratische Funktionen parabelförmige Kurven. Eine Parabel ist diese U-förmige Linie, die du vielleicht schon mal gesehen hast. Die allgemeine Form einer quadratischen Funktion lautet: f(x) = ax² + bx + c, wobei a, b und c Konstanten sind. Das "a" vor dem x² ist besonders wichtig, denn es bestimmt, ob die Parabel nach oben (a > 0) oder nach unten (a < 0) geöffnet ist. Stell dir vor, "a" ist wie ein Daumen nach oben oder unten für die Kurve!

Aber warum ist das wichtig? Weil viele Dinge in der realen Welt parabelförmige Bahnen beschreiben. Denke an einen Ball, den du wirfst. Oder das Wasser, das aus einem Springbrunnen schießt. Quadratische Funktionen helfen uns, diese Bewegungen zu verstehen und vorherzusagen.

Die Lösungssuche: Nullstellen und Co.

Die Nullstellen einer quadratischen Funktion sind die x-Werte, bei denen die Funktion den Wert null annimmt (also die Stellen, wo die Parabel die x-Achse schneidet). Diese zu finden, ist oft der Schlüssel zur Lösung von Aufgaben.

Es gibt verschiedene Methoden, um diese Nullstellen zu finden:

• Die Mitternachtsformel (oder abc-Formel): Der Klassiker! Sie funktioniert immer und lautet: x = (-b ± √(b² - 4ac)) / 2a. Ja, sie ist etwas lang, aber sie ist dein bester Freund, wenn du mal nicht weiterweißt.
• Die p-q-Formel: Eine vereinfachte Version der Mitternachtsformel, wenn deine quadratische Funktion in der Form x² + px + q = 0 vorliegt.
• Faktorisierung: Wenn du Glück hast, kannst du die quadratische Funktion in zwei lineare Faktoren zerlegen. Das ist oft der schnellste Weg, aber er funktioniert nicht immer.
• Quadratische Ergänzung: Eine Methode, die dir hilft, die Funktion in eine Form zu bringen, aus der du die Nullstellen direkt ablesen kannst.

Tipp: Übung macht den Meister! Je mehr Aufgaben du löst, desto intuitiver wird es, die richtige Methode zu wählen.

Anwendungsbeispiele mit Lösungen

Okay, genug Theorie. Lass uns das Ganze an einem Beispiel festmachen:

Aufgabe: Eine Brücke hat eine parabelförmige Form. Der höchste Punkt der Brücke liegt 20 Meter über der Fahrbahn und befindet sich in der Mitte der Brücke. Die Brücke ist insgesamt 40 Meter breit. Bestimme die Gleichung der Parabel, die die Form der Brücke beschreibt.

Lösung:

1. Wir legen den Ursprung des Koordinatensystems in die Mitte der Brücke auf der Fahrbahn.
2. Der höchste Punkt der Parabel (der Scheitelpunkt) liegt dann bei (0, 20).
3. Die Parabel schneidet die x-Achse bei (-20, 0) und (20, 0).
4. Wir wissen, dass die allgemeine Form einer Parabel f(x) = a(x - h)² + k ist, wobei (h, k) der Scheitelpunkt ist.
5. In unserem Fall ist (h, k) = (0, 20), also f(x) = a(x - 0)² + 20 = ax² + 20.
6. Um "a" zu bestimmen, setzen wir einen der Nullpunkte ein, z.B. (20, 0): 0 = a(20)² + 20.
7. Daraus folgt: -20 = 400a, also a = -1/20.
8. Die Gleichung der Parabel lautet also: f(x) = (-1/20)x² + 20.

Wichtig: Vergewissere dich immer, dass deine Lösung Sinn ergibt. In diesem Fall sollte die Parabel nach unten geöffnet sein (a < 0), da die Brücke eine nach unten gewölbte Form hat.

Quadratische Funktionen im Alltag: Mehr als nur Mathe

Du denkst vielleicht, quadratische Funktionen sind nur etwas für den Matheunterricht, aber sie begegnen uns überall. Sie stecken in der Architektur von Gebäuden, der Optimierung von Produktionsprozessen und sogar in der Finanzmathematik. Denk an Achterbahnen – ihre Loopings sind oft perfekt parabelförmig!

Kleiner Fun Fact: Wusstest du, dass Galileo Galilei quadratische Funktionen nutzte, um die Bewegung von Projektilen zu beschreiben?

Fazit: Nicht perfekt sein, sondern anfangen!

Quadratische Funktionen mögen anfangs einschüchternd wirken, aber mit etwas Übung und den richtigen Werkzeugen (wie der Mitternachtsformel!) kannst du sie meistern. Und vergiss nicht: Es geht nicht darum, alles sofort perfekt zu können, sondern darum, anzufangen und Schritt für Schritt zu lernen. Und wer weiß, vielleicht entdeckst du ja sogar die Schönheit hinter diesen Kurven und Gleichungen. Stell dir vor, du könntest die Flugbahn eines Fußballs berechnen…ziemlich cool, oder?