Berechnung Umfang Eines Kreises Formel

Hey du! Schon mal einen Kreis umarmt? Wahrscheinlich nicht, aber hast du dich jemals gefragt, wie lang so eine Umarmung wäre? Keine Sorge, wir müssen jetzt keine Maßbänder an Torten halten. Stattdessen tauchen wir in die super-praktische (und ja, sogar spaßige!) Welt des Kreisumfangs ein. Und das mit einer Formel, die einfacher ist, als du denkst.

Was genau ist der Umfang? Stell dir vor, du bist eine Ameise, die einmal komplett um einen Pizza-Rand krabbelt. Die Strecke, die du zurücklegst, das ist der Umfang. Einfach, oder?

Warum solltest du das wissen wollen?

Okay, ich hör dich schon: "Umfang? Brauche ich das wirklich im Alltag?" Aber warte mal! Denk an all die runden Dinge, die uns ständig umgeben: Fahrräder, Uhren, Pfannkuchen, Autoräder... Verstehst du jetzt? Das Wissen um den Umfang kann in überraschend vielen Situationen nützlich sein. Hier ein paar Beispiele:

Pizza-Party: Du willst wissen, ob genug Pizza für alle da ist? Mit dem Umfang kannst du abschätzen, wie viel Belag du insgesamt brauchst.
Garten-Projekt: Du baust ein kreisförmiges Blumenbeet und brauchst die richtige Länge für den Zaun? Der Umfang hilft!
Fahrrad-Reparatur: Du musst einen neuen Reifen kaufen und brauchst die richtige Größe? Rat mal, was du dafür brauchst...

Also, ja, der Umfang ist nützlicher, als du vielleicht denkst! Und jetzt kommt der beste Teil: die Formel, die dir das Leben leichter macht.

Die magische Formel: U = 2 * π * r

Klingt kompliziert? Keine Panik! Lass uns das aufschlüsseln:

U steht für den Umfang (logisch, oder?).
π (Pi) ist eine ganz besondere Zahl. Sie ist ungefähr 3,14. Merk dir das, das ist dein neuer bester Freund!
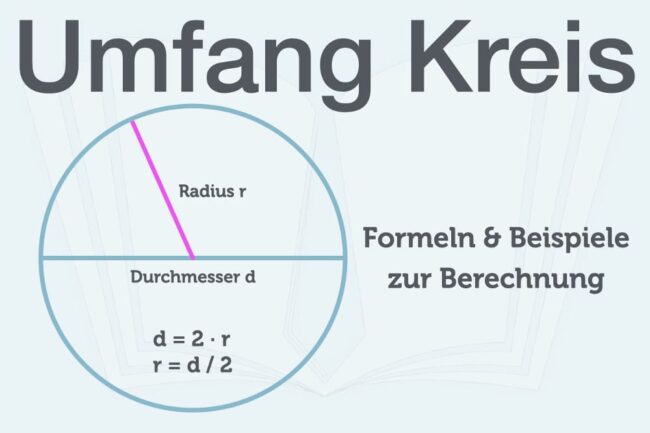
r steht für den Radius. Das ist die Hälfte des Durchmessers des Kreises. Stell dir vor, du ziehst eine Linie von der Mitte des Kreises bis zum Rand – das ist der Radius.

Also, die Formel sagt: Um den Umfang eines Kreises zu berechnen, nimmst du den Radius, multiplizierst ihn mit 2 und dann mit Pi (3,14). Das ist alles!

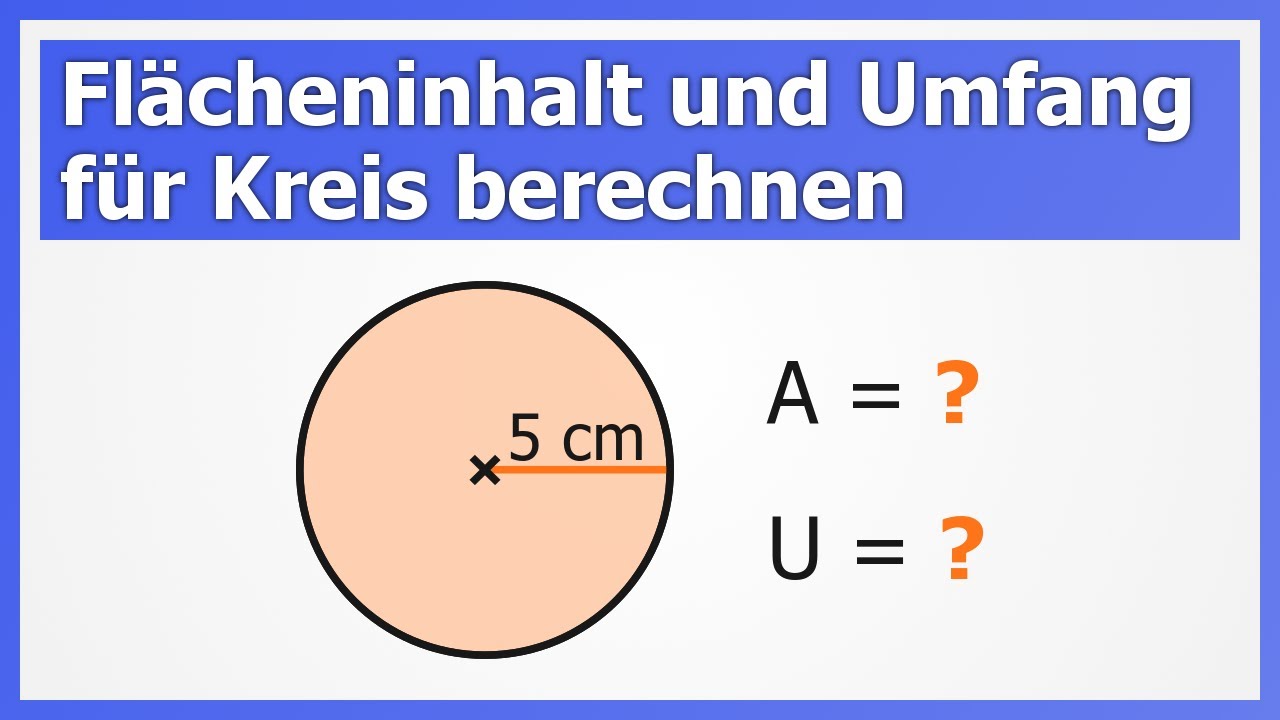
Ein Beispiel gefällig? Nehmen wir an, deine Pizza hat einen Radius von 15 cm. Dann ist der Umfang: U = 2 * 3,14 * 15 = 94,2 cm. Das ist eine ganz schön lange Pizza-Umarmung!

Der Durchmesser kommt ins Spiel

Manchmal kennst du nicht den Radius, sondern den Durchmesser (die Linie, die einmal quer durch den Kreis geht und durch die Mitte verläuft). Keine Sorge, auch dafür gibt es eine Lösung! Der Durchmesser ist einfach das Doppelte des Radius. Also: d = 2 * r.

Daraus ergibt sich eine alternative Formel für den Umfang: U = π * d. Du multiplizierst einfach Pi mit dem Durchmesser. Super einfach!

Beispiel: Ein rundes Planschbecken hat einen Durchmesser von 2 Metern. Der Umfang ist dann: U = 3,14 * 2 = 6,28 Meter. Das ist die Länge des Planschbecken-Randes, an dem du deine Handtücher aufhängen kannst.

Pi: Die unendliche Geschichte

Wir haben Pi (π) schon kurz erwähnt. Aber diese Zahl ist so faszinierend, dass sie eine eigene kleine Geschichte verdient. Pi ist eine sogenannte irrationale Zahl. Das bedeutet, dass sie unendlich viele Nachkommastellen hat und sich nie wiederholt. Die ersten paar Stellen sind 3,1415926535... und sie geht immer weiter! Mathematiker haben bereits Billionen von Stellen von Pi berechnet, aber es gibt immer noch kein Ende.

Denk mal drüber nach, während du das nächste Mal einen Kreis betrachtest: Da steckt eine unendliche Geschichte drin!

Warum das alles wichtig ist

Okay, vielleicht wirst du jetzt nicht jeden Tag den Umfang eines Kreises berechnen. Aber das Verständnis für grundlegende mathematische Konzepte wie den Umfang hilft dir, die Welt um dich herum besser zu verstehen. Es schärft dein logisches Denken und gibt dir Werkzeuge an die Hand, um Probleme zu lösen.

Und ganz ehrlich, es ist doch auch cool, zu wissen, dass du die Länge der Pizza-Umarmung berechnen kannst, oder?

Also, das nächste Mal, wenn du einen Kreis siehst, denk an Pi, den Radius und die einfache, aber mächtige Formel, die dir hilft, den Umfang zu berechnen. Wer weiß, wann du dieses Wissen mal brauchen wirst! Und wer weiß, vielleicht motiviert dich das sogar, ein bisschen mehr über Mathematik zu lernen. Denn Mathematik ist überall – und sie kann sogar Spaß machen!