Bestimme An Welchen Stellen Die Quadratfunktion Den Wert 4 Annimmt

Okay, mal ehrlich: Mathe kann manchmal so sein wie der Versuch, Spaghetti mit Essstäbchen zu essen. Man versteht zwar, *was* man tun soll, aber *wie* man es anstellt, ist ein ganz anderes Thema. Und Quadratfunktionen klingen erstmal nach etwas, was in einem Raumschiff verbaut wird, aber keine Panik! Eigentlich sind sie gar nicht so gruselig. Denkt einfach an eine sanfte, U-förmige Kurve. Mehr nicht.

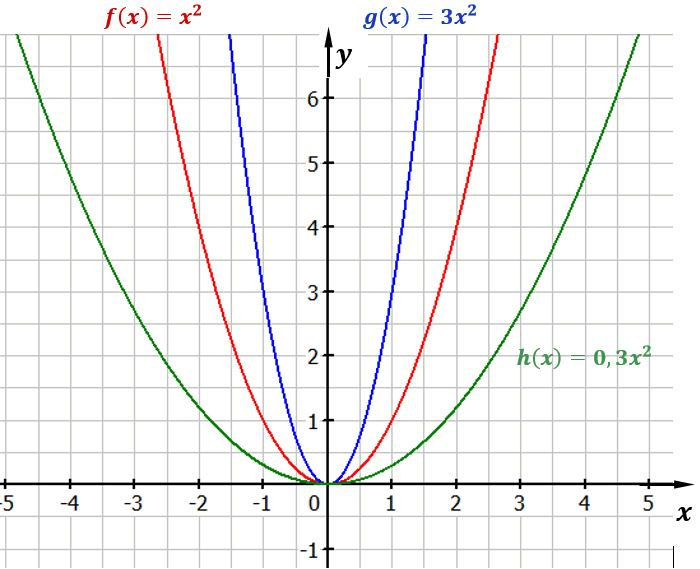
Quadratfunktionen im echten Leben – Mehr als nur Zahlen!

Ihr fragt euch jetzt sicher: "Wozu brauche ich das denn überhaupt?" Nun, überlegt mal: Habt ihr schon mal einen Ball geworfen? Oder eine Achterbahnfahrt genossen? Die Flugbahn des Balls und die Auf- und Abfahrten der Achterbahn lassen sich mit Quadratfunktionen beschreiben! Sie sind überall, nur verstecken sie sich gut.

Und heute kümmern wir uns um eine ganz spezielle Frage: Wo genau nimmt diese U-förmige Kurve den Wert 4 an? Stell dir vor, die U-Kurve ist eine Landkarte, und wir suchen die Orte, wo die Höhe 4 Meter beträgt. Klingt doch machbar, oder?

Was bedeutet "den Wert 4 annehmen"?

Ganz einfach: Wir suchen die x-Werte (die horizontalen Positionen), bei denen die Funktion y = 4 liefert. Mit anderen Worten: Wenn wir diese x-Werte in unsere Quadratfunktion einsetzen, muss 4 herauskommen. Klingt kompliziert, ist es aber eigentlich nicht. Denkt an ein Rezept: Wir suchen die Zutaten (x-Werte), die am Ende zum perfekten Kuchen (Wert 4) führen.

Die Werkzeuge, die wir brauchen

Keine Sorge, wir brauchen keine Raketenwissenschaft. Wir brauchen eigentlich nur ein paar grundlegende mathematische Werkzeuge:

• Die Quadratfunktion selbst: Die hat meistens die Form f(x) = ax² + bx + c. a, b und c sind einfach nur Zahlen.
• Eine Gleichung: Wir stellen die Gleichung f(x) = 4 auf.
• Ein bisschen Algebra: Um die Gleichung zu lösen. Keine Angst, ich verspreche, es wird nicht allzu schmerzhaft.

Schritt-für-Schritt Anleitung (mit einem Augenzwinkern)

Okay, los geht's! Nehmen wir mal an, unsere Quadratfunktion ist f(x) = x² - 2x + 1. Ein ganz harmloses Exemplar, quasi der Pudel unter den Quadratfunktionen.

1. Gleichung aufstellen: Wir wollen wissen, wann f(x) = 4 ist. Also schreiben wir: x² - 2x + 1 = 4.
2. Null auf einer Seite: Wir wollen die Gleichung so umformen, dass auf einer Seite eine Null steht. Also subtrahieren wir 4 von beiden Seiten: x² - 2x - 3 = 0.
3. Lösen, Baby! Jetzt gibt es verschiedene Möglichkeiten, das Biest zu zähmen:
   • Faktorisieren: Wenn wir Glück haben, können wir die Gleichung in zwei Klammern aufteilen. In diesem Fall klappt's: (x - 3)(x + 1) = 0. Das bedeutet, entweder x - 3 = 0 oder x + 1 = 0. Also ist x = 3 oder x = -1.
   • Die Mitternachtsformel (oder abc-Formel): Wenn Faktorisieren nicht klappt (was oft der Fall ist, seien wir ehrlich), kommt die Mitternachtsformel ins Spiel. Sie ist zwar ein bisschen länger, aber sie funktioniert *immer*. Ich erspare euch hier die Details, aber ihr könnt sie googeln. Sie spuckt euch die Lösungen für x aus.
   • Quadratische Ergänzung: Ein bisschen komplizierter, aber auch eine Option. Wie das perfekte Geheimrezept der Oma, das keiner so richtig versteht.

Ergebnis: In unserem Beispiel haben wir herausgefunden, dass die Quadratfunktion f(x) = x² - 2x + 1 den Wert 4 an den Stellen x = 3 und x = -1 annimmt. Juhu! Wir haben die Schätze auf unserer Landkarte gefunden!

Fazit: Keine Angst vor der U-Kurve!

Ihr seht also, es ist gar nicht so schwer, herauszufinden, wo eine Quadratfunktion einen bestimmten Wert annimmt. Mit ein bisschen Übung und den richtigen Werkzeugen ist das wie ein Spaziergang im Park – okay, vielleicht ein Spaziergang durch einen Park mit kleinen Mathe-Hügeln, aber trotzdem machbar! Und denkt dran: Wenn ihr mal nicht weiterkommt, gibt es immer jemanden, der euch helfen kann. Fragt eure Freunde, Lehrer oder das Internet. Und vor allem: Habt Spaß dabei!

Und jetzt: Viel Erfolg beim Finden eurer x-Werte! 😉