Brüche Erweitern Und Kürzen Arbeitsblätter
Wisst ihr, ich hatte mal so eine Mathelehrerin, Frau Schmidt… die war echt der Knaller. Nicht im positiven Sinne. Die hat uns immer mit so trockenen Aufgaben gequält, besonders Brüche. Ich hab's gehasst! "Kürzen Sie diesen Bruch!" oder "Erweitern Sie gefälligst!"... es klang wie eine Kriegserklärung. Aber, hey, zumindest bin ich nicht ganz dumm gestorben, oder? Und heute reden wir ja auch drüber – Brüche erweitern und kürzen, aber ganz entspannt.
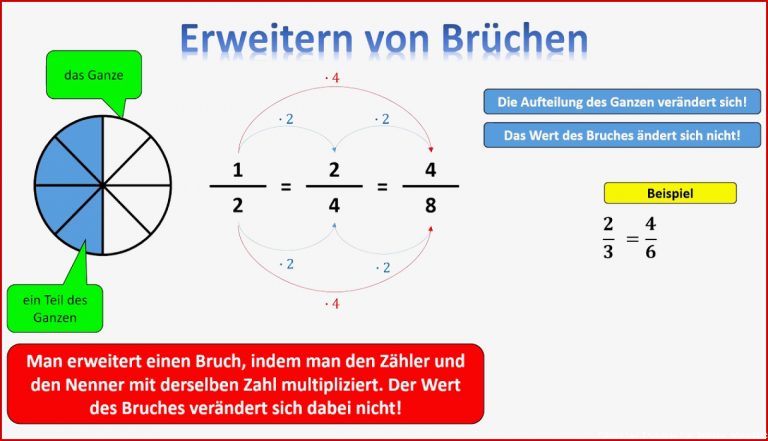
Worum geht's also? Im Grunde ist das Erweitern und Kürzen von Brüchen nichts anderes als Magie. Nein, Quatsch! Aber es fühlt sich manchmal so an. Stell dir vor, du hast ein Stück Kuchen. Sagen wir, die Hälfte davon. 1/2, ganz einfach. Wenn du dieses Kuchenstück jetzt in zwei gleich große Teile schneidest, hast du vier Stücke, und du hast zwei davon. Also 2/4. Aber hey, du hast trotzdem noch die gleiche Menge Kuchen gegessen! Das ist der Trick beim Erweitern und Kürzen. Du veränderst nur die Darstellung, nicht den Wert.
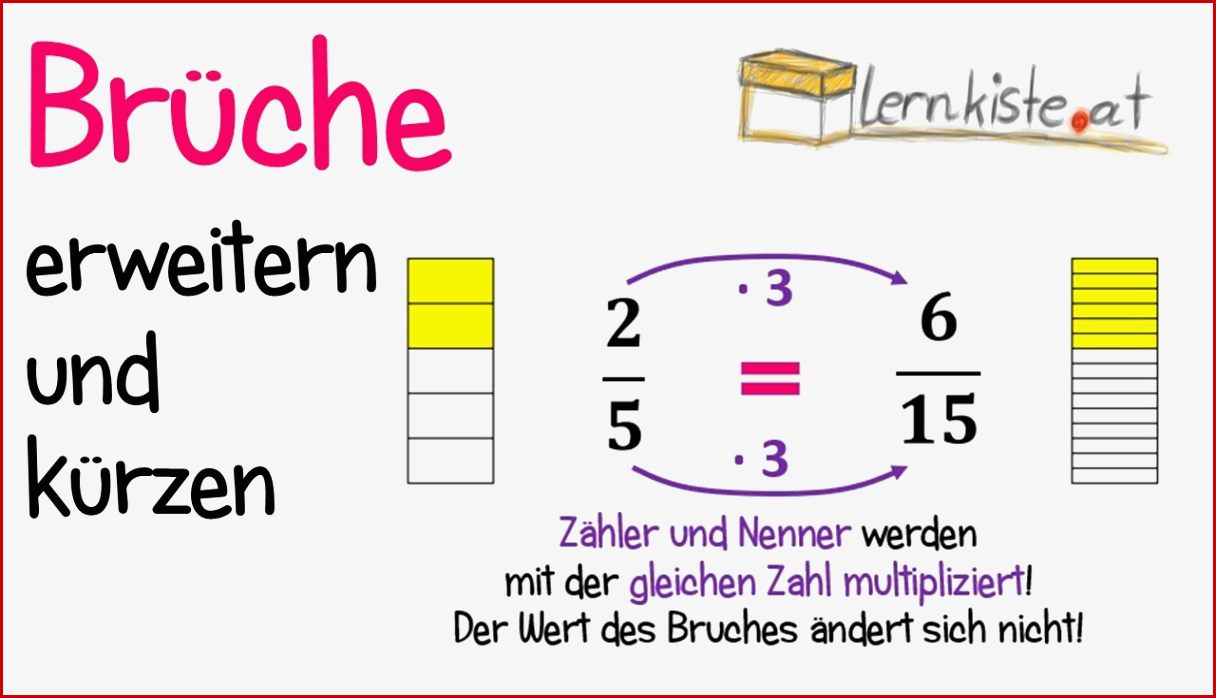
Erweitern bedeutet, dass du den Zähler (die Zahl oben im Bruch) und den Nenner (die Zahl unten) mit der gleichen Zahl multiplizierst. Warum? Weil du den Wert des Bruches nicht ändern willst! Wenn du nur den Zähler verdoppelst, hättest du plötzlich doppelt so viel Kuchen! Und das wäre ja unfair, oder?
Beispiel: 1/3 erweitern mit 2. Das wäre dann (1*2)/(3*2) = 2/6. Boom! Gleiche Menge Kuchen, nur anders aufgeteilt.
Kürzen ist das Gegenteil von Erweitern. Du teilst Zähler und Nenner durch die gleiche Zahl. Ziel ist meistens, den Bruch so einfach wie möglich darzustellen. Stell dir vor, du hast 4/8 Kuchen. Das kannst du locker auf 1/2 kürzen, indem du beide Zahlen durch 4 teilst. Viel übersichtlicher, oder?
Beispiel: 6/9 kürzen mit 3. Das wäre dann (6/3)/(9/3) = 2/3. Wieder einmal: Gleiche Menge Kuchen, aber in simpler Form. Wer will schon komplizierte Kuchen?
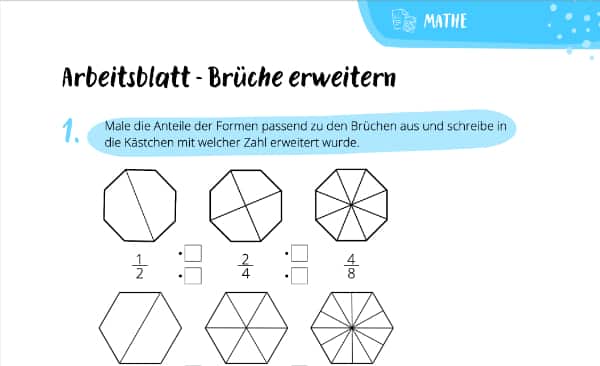
Und wo kommen jetzt die Arbeitsblätter ins Spiel? Na ja, Übung macht den Meister! Oder in diesem Fall den Bruchrechen-Meister. Mit Arbeitsblättern kannst du das Erweitern und Kürzen üben, bis du es im Schlaf kannst. Und keine Angst, es gibt mittlerweile echt coole Arbeitsblätter, nicht nur so trockene wie bei Frau Schmidt damals. Viele sind sogar spielerisch gestaltet. (Ich hätte damals alles für spielerische Arbeitsblätter gegeben!)
Warum sind diese Arbeitsblätter so wichtig? Weil sie dir helfen, ein Gefühl für Brüche zu entwickeln. Du lernst Muster zu erkennen, Zusammenhänge zu verstehen und irgendwann denkst du gar nicht mehr drüber nach. Dann ist das Erweitern und Kürzen wie Fahrradfahren – du kannst es einfach.
Und was ist das Ziel? Das Ziel ist nicht nur, gute Noten in Mathe zu bekommen (obwohl das natürlich auch super ist!). Das Ziel ist, dass du Mathe verstehst. Dass du sie nicht als eine Reihe von sinnlosen Regeln siehst, sondern als ein Werkzeug, mit dem du die Welt um dich herum besser verstehen kannst. (Klingt pathetisch, ist aber so!)
Also, ran an die Arbeitsblätter! Keine Angst vor Fehlern, die sind zum Lernen da. Und wenn du mal nicht weiterweißt, frag jemanden um Hilfe. Oder schau dir ein Erklärvideo an. Oder lies diesen Artikel nochmal! 😉 Es gibt viele Wege, um Bruchrechen-Meister zu werden.
Und denk dran: Selbst wenn du nie wieder einen Bruch in deinem Leben erweitern oder kürzen musst, hast du etwas Wichtiges gelernt: Probleme zu lösen. Und das ist eine Fähigkeit, die dir in allen Bereichen des Lebens helfen wird. (Also, danke Frau Schmidt! Irgendwie...)
Tipps für die Arbeit mit Brüchen-Arbeitsblättern
* Fang einfach an: Suche dir Arbeitsblätter mit einfachen Brüchen aus. Steigere den Schwierigkeitsgrad langsam. * Schreibe alles auf: Notiere dir alle Rechenschritte. So kannst du Fehler besser finden. * Kontrolliere deine Ergebnisse: Nutze einen Taschenrechner oder eine Lösungsübersicht, um deine Ergebnisse zu überprüfen. * Mach Pausen: Wenn du frustriert bist, leg das Arbeitsblatt weg und mach etwas anderes. * Hab Spaß! Ja, Mathe kann Spaß machen! Such dir lustige Arbeitsblätter oder bearbeite sie mit Freunden.