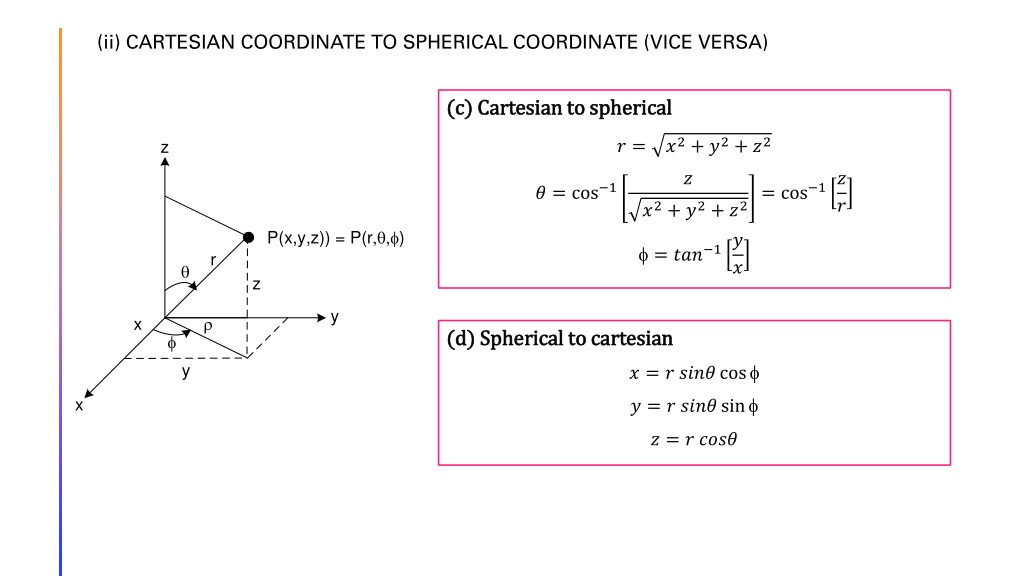
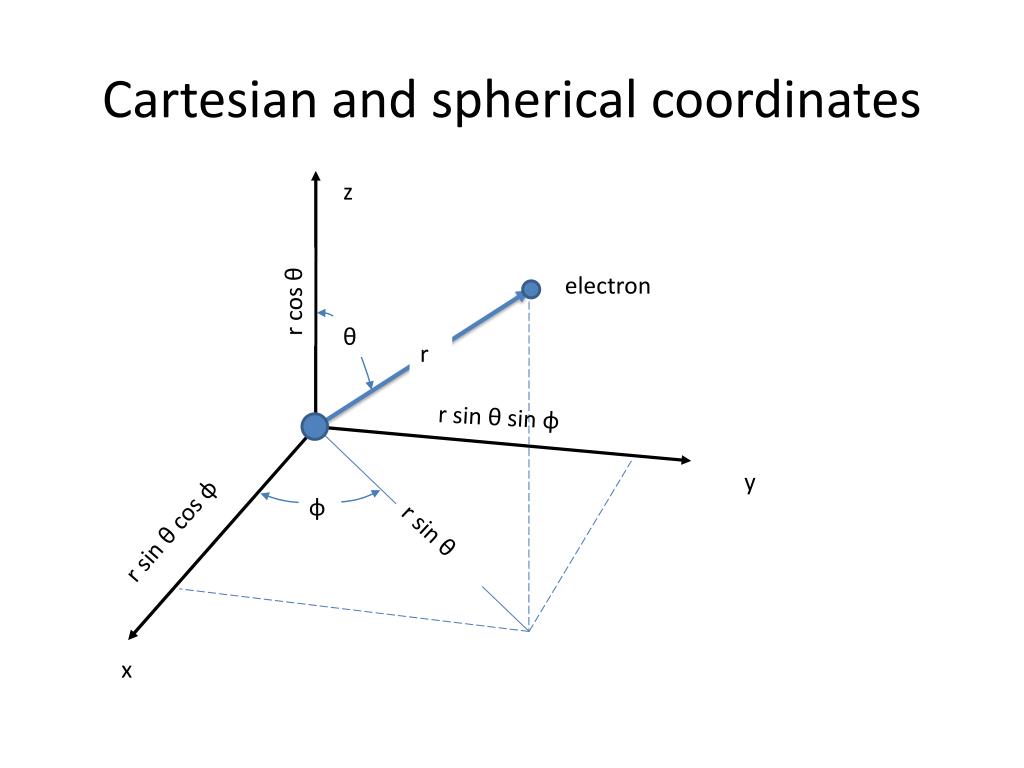
Cartesian Coordinates To Spherical Coordinates
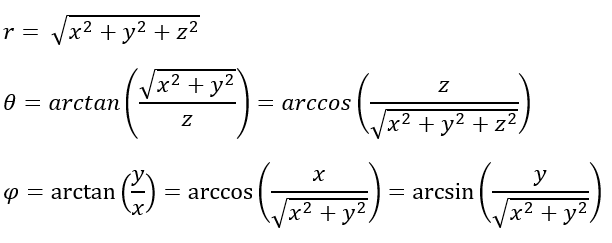
Hast du dich jemals gefragt, wie Navigationssysteme in Flugzeugen oder Computerspiele funktionieren, die uns dreidimensionale Welten zeigen? Ein Schlüssel dazu ist die Umwandlung von Koordinatensystemen. Heute tauchen wir ein in ein besonders interessantes Beispiel: die Umwandlung von kartesischen Koordinaten in sphärische Koordinaten. Keine Angst, es klingt komplizierter als es ist! Es ist wie das Erlernen einer neuen Sprache, die uns hilft, die Welt um uns herum auf neue Weise zu beschreiben.
Warum ist das überhaupt relevant oder gar "fun"? Stell dir vor, du bist ein Astrophysiker, der die Position eines Sterns beschreiben muss. Kartesische Koordinaten (x, y, z) wären möglich, aber unglaublich unhandlich! Die Entfernung vom Ursprung und die Winkel, die der Stern relativ zu einer Referenzrichtung einnimmt, wären viel intuitiver. Genau das leisten sphärische Koordinaten (ρ, θ, φ): ρ ist der Radius (Entfernung vom Ursprung), θ ist der Azimutwinkel (wie weit nach links oder rechts) und φ ist der Polarwinkel (wie weit nach oben oder unten).
Der Zweck dieser Umwandlung ist es, eine flexiblere und oft intuitivere Art zu bieten, Punkte im dreidimensionalen Raum zu beschreiben. Die Vorteile sind vielfältig. Erstens vereinfacht es die Beschreibung von Objekten mit sphärischer Symmetrie, wie Kugeln oder Sterne. Zweitens erleichtert es viele mathematische Berechnungen, insbesondere in der Physik und Ingenieurwissenschaft. Drittens bietet es eine direktere Verbindung zu unserer intuitiven Vorstellung von Richtung und Entfernung.
Beispiele finden sich überall. In der Bildung werden sie verwendet, um Studenten die Geometrie im dreidimensionalen Raum näherzubringen und das Verständnis für Konzepte wie Vektoren und Transformationen zu vertiefen. In der Computergrafik sind sie essenziell für die Modellierung von 3D-Objekten und das Rendern von Szenen. Denk an die Programmierung eines Roboters, der sich in einem Raum bewegt. Die Programmierung, dass er eine bestimmte Entfernung zurücklegen und sich in einem bestimmten Winkel drehen soll, ist einfacher mit sphärischen Koordinaten.
Und was ist mit dem täglichen Leben? Navigationssysteme verwenden komplexe Algorithmen, die oft auf sphärischen Koordinaten basieren, um die Position von Flugzeugen oder Schiffen zu bestimmen. Auch bei der Positionsbestimmung von Satelliten spielen sie eine wichtige Rolle. Wenn du also das nächste Mal ein GPS benutzt, denk daran, dass hinter den Kulissen eine Menge Mathematik abläuft, die auf diesen Koordinaten basiert!
Wie kann man diese Konzepte praktisch erkunden? Eine einfache Möglichkeit ist, mit einer 3D-Grafiksoftware oder einem Programm wie GeoGebra 3D zu spielen. Gib kartesische Koordinaten ein und beobachte, wie sie in sphärische Koordinaten umgewandelt werden. Versuche, die sphärischen Koordinaten zu verändern und zu sehen, wie sich der Punkt im Raum bewegt. Du kannst auch versuchen, ein kleines Python-Skript zu schreiben, das die Umwandlung durchführt. Viele Online-Rechner bieten ebenfalls eine einfache Möglichkeit, kartesische Koordinaten in sphärische zu konvertieren. Hab keine Angst, einfach auszuprobieren und zu experimentieren! Das Wichtigste ist, ein Gefühl dafür zu bekommen, wie die beiden Koordinatensysteme zusammenhängen.
Es mag zunächst abschreckend wirken, aber mit ein wenig Übung und Neugier wirst du bald feststellen, dass die Umwandlung von kartesischen in sphärische Koordinaten ein mächtiges Werkzeug ist, um die Welt um uns herum besser zu verstehen. Viel Spaß beim Entdecken!