Continuous Uniform Distribution Variance
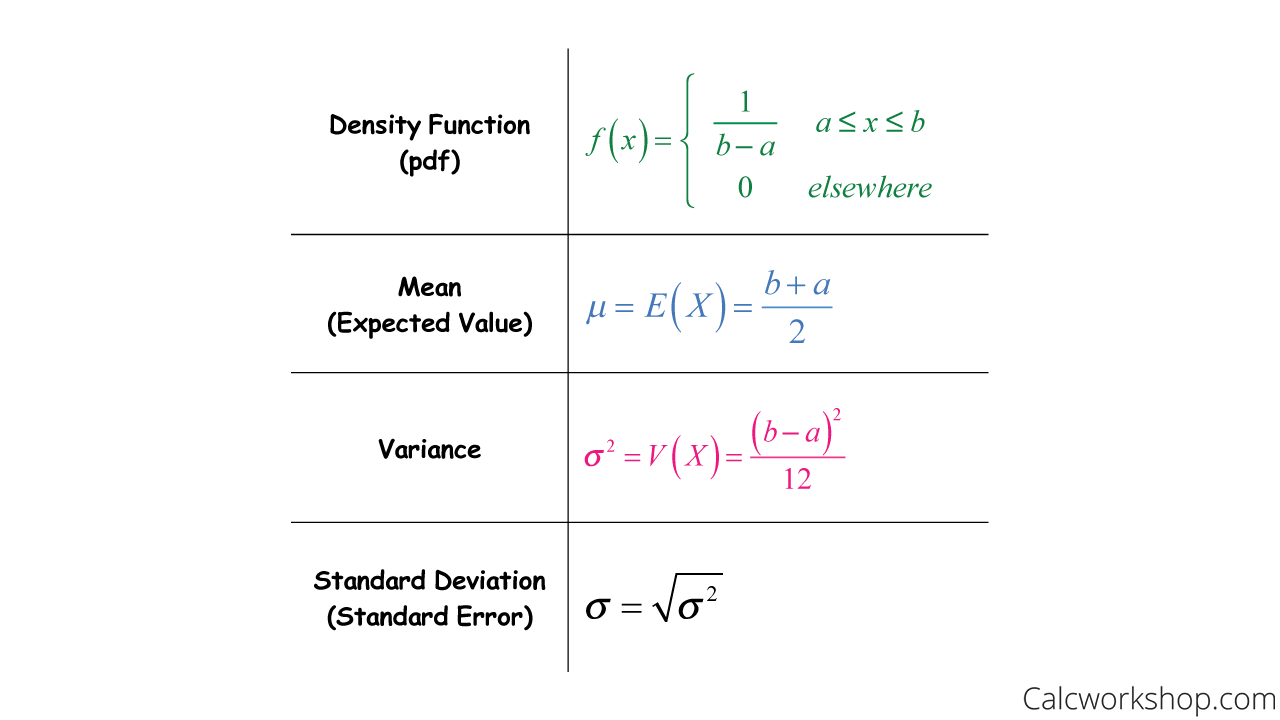
Hallo, Statistik-Freunde! Lasst uns heute mal so richtig in die Vollen gehen mit einer Verteilung, die so einfach ist, dass selbst mein Goldfisch (er heißt übrigens *Professor Flosse*) sie versteht: Die kontinuierliche Gleichverteilung! Und weil's so schön ist, gucken wir uns auch gleich die Varianz an. Keine Angst, es wird nicht staubtrocken. Versprochen!
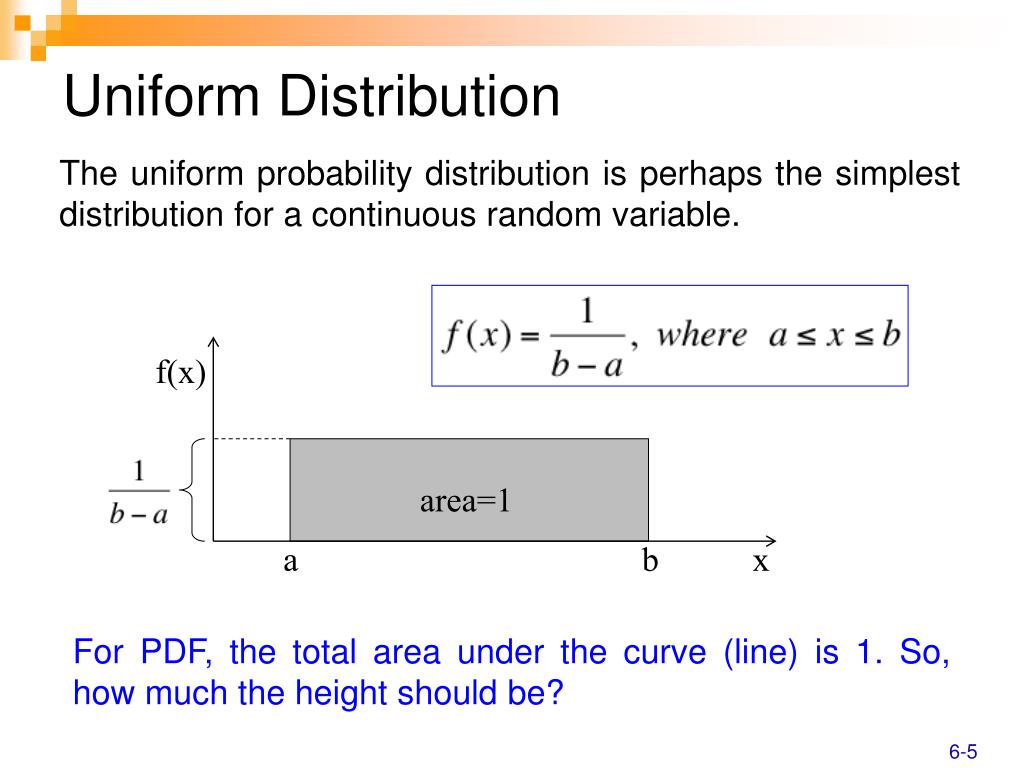
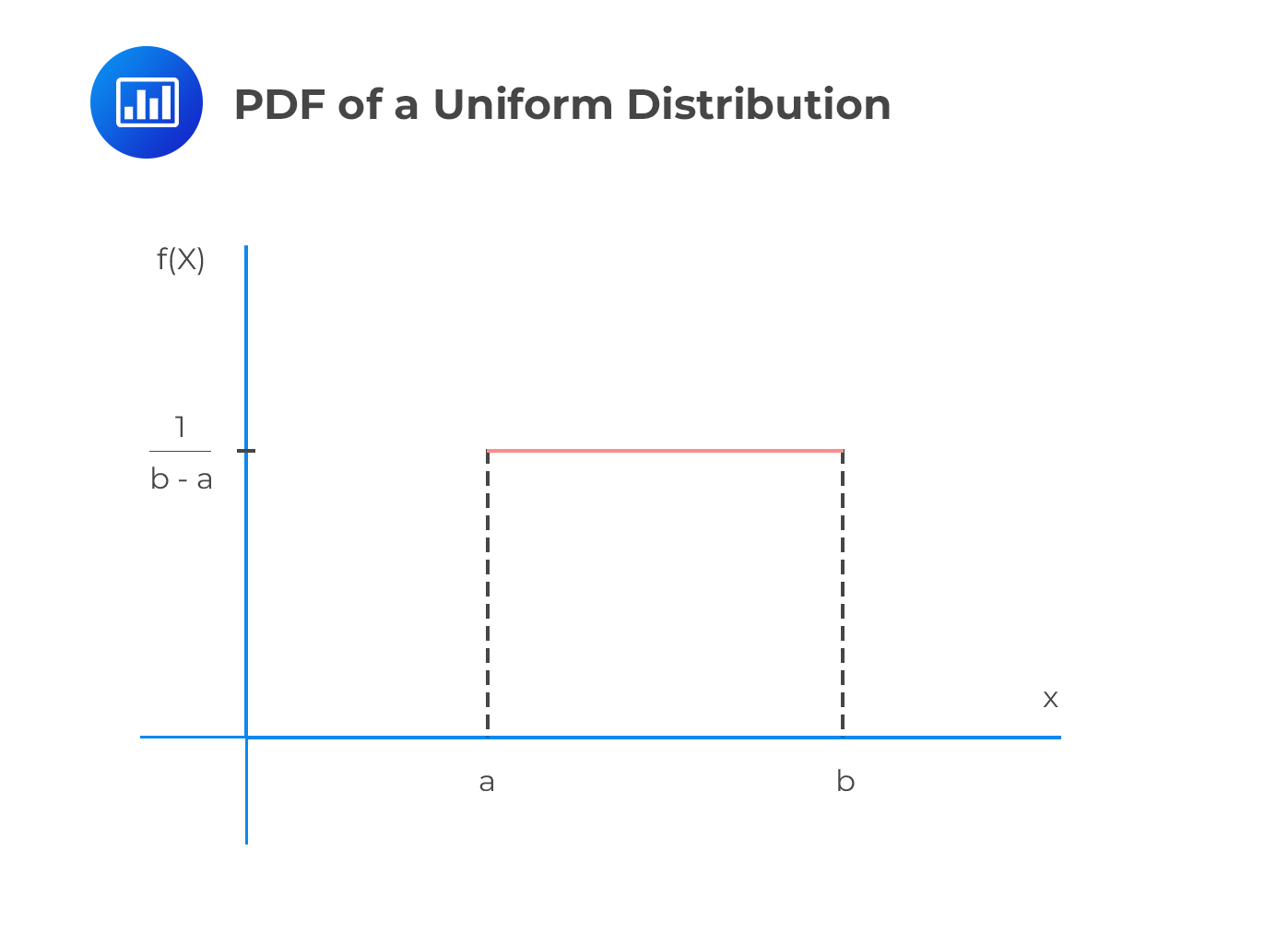
Was ist denn diese Gleichverteilung überhaupt?
Stellt euch vor, ihr seid bei einem Karnevalsspiel. Es gibt ein Glücksrad, das perfekt ausbalanciert ist. Es zeigt Zahlen von 0 bis 10 an. Jede Zahl hat die genau gleiche Chance, ausgewählt zu werden. Das ist die Essenz der Gleichverteilung! Keine Zahl wird bevorzugt, keine Zahl hat Angst vor dem Ausgestoßen-werden. Pure, mathematische Demokratie!
In der echten Welt könnte das zum Beispiel die Wartezeit auf einen Bus sein, der theoretisch alle 15 Minuten fährt. Wenn der Busfahrer ein absoluter Chaot ist und sich überhaupt nicht an den Fahrplan hält (hey, das passiert!), dann ist jede Wartezeit zwischen 0 und 15 Minuten gleich wahrscheinlich. Drama, Baby!
Die Varianz: Das Maß der Unordnung (oder eben nicht!)
Okay, jetzt kommt der Clou. Die Varianz. Keine Panik, das klingt schlimmer als es ist. Die Varianz ist einfach ein Maß dafür, wie weit die Werte im Durchschnitt vom Mittelwert entfernt liegen. Je größer die Varianz, desto stärker streuen die Werte. Je kleiner, desto mehr kuscheln sie sich um den Mittelwert.
Bei unserer Gleichverteilung ist die Varianz ein bisschen wie der Grad der Langeweile. Wenn alle Werte immer gleich sind (zum Beispiel immer 5), dann ist die Varianz 0. Super langweilig! Aber wenn die Werte wild durcheinander purzeln (0, 1, 2, 3, 4…), dann ist die Varianz größer. Ein bisschen mehr Action!
Die Formel, die gar nicht so gruselig ist
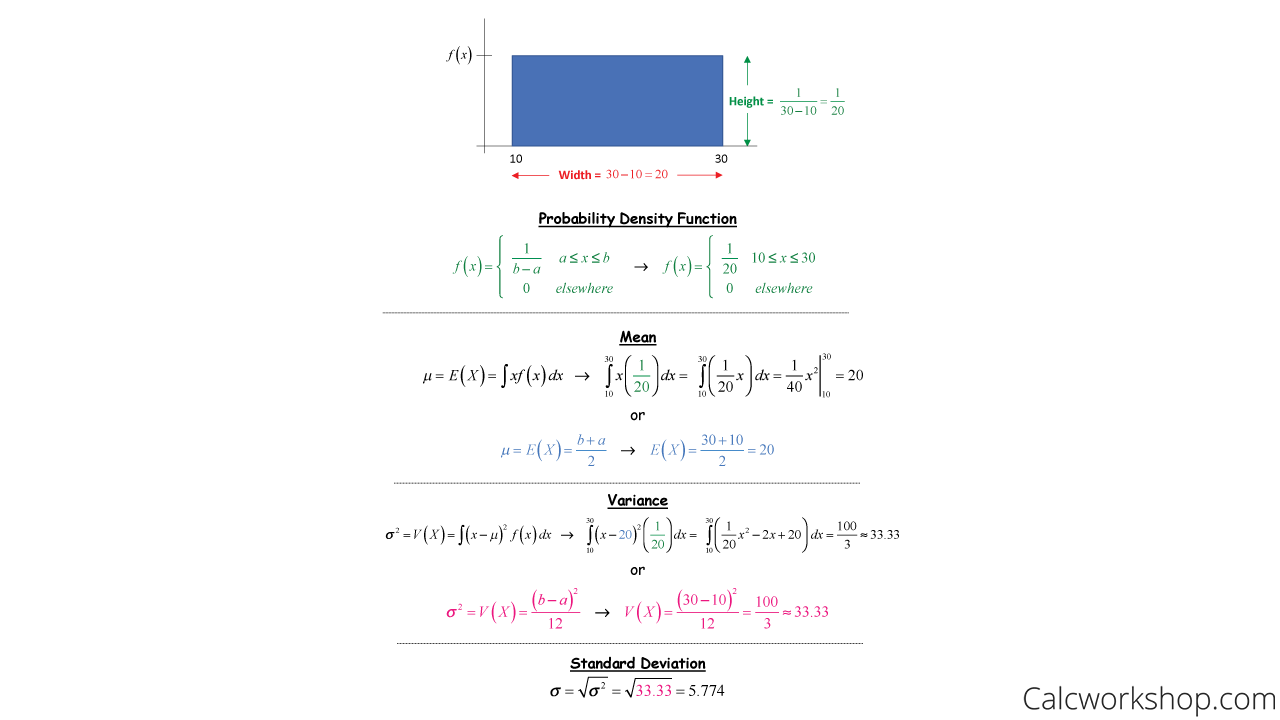
Jetzt kommt der Moment, vor dem sich manche fürchten: Die Formel! Aber keine Sorge, ich hab sie schon gezähmt. Für eine Gleichverteilung zwischen den Werten *a* und *b* (zum Beispiel 0 und 10 bei unserem Glücksrad) ist die Varianz:
Varianz = (b - a)² / 12
Ja, das war's schon! Super easy, oder? Keine Wurzeln, keine komplizierten Integrale (phew!). Einfach nur *b* minus *a*, das Ergebnis quadriert und dann durch 12 geteilt. Ich wiederhole: Super easy!
Lasst uns das mal an unserem Glücksrad-Beispiel ausprobieren. *a* ist 0, *b* ist 10. Also:
Varianz = (10 - 0)² / 12 = 100 / 12 = 8.33
Das bedeutet, dass die durchschnittliche Abweichung vom Mittelwert (der in diesem Fall 5 ist) ungefähr 8.33 beträgt. Nicht schlecht, für ein Glücksrad, das sich so unparteiisch gibt!
Ein weiteres Beispiel, nur zum Spaß
Nehmen wir an, ihr verkauft Eis. Und zwar nur zwischen 14 und 16 Uhr (komische Geschäftszeiten, ich weiß, aber bleiben wir mal dabei). Sagen wir, die Eisverkäufe sind zwischen diesen Zeiten gleichverteilt. Dann ist *a* = 14 und *b* = 16.
Varianz = (16 - 14)² / 12 = 4 / 12 = 0.33
Eine relativ geringe Varianz! Das bedeutet, eure Eisverkäufe schwanken nicht so stark um den Mittelwert herum. Ihr könnt also relativ genau vorhersagen, wie viel Eis ihr verkaufen werdet (was ziemlich cool ist, wenn man Eisverkäufer ist).
Warum ist das Ganze überhaupt wichtig?
Okay, die große Frage: Warum sollten wir uns überhaupt für die Varianz einer Gleichverteilung interessieren? Nun, die Gleichverteilung ist ein Grundbaustein in der Statistik. Sie wird oft als Basis für Simulationen und Modellierungen verwendet. Wenn man die Varianz kennt, kann man besser einschätzen, wie realistisch die Ergebnisse sind.
Außerdem hilft die Varianz uns, Risiken einzuschätzen. Wenn die Varianz hoch ist, bedeutet das, dass es ein größeres Risiko gibt, dass die tatsächlichen Werte stark vom erwarteten Wert abweichen. Und das ist gut zu wissen, egal ob man Glücksräder dreht, Eis verkauft oder einfach nur versucht, sein Leben zu planen.
Also, das war's! Die kontinuierliche Gleichverteilung und ihre Varianz. Ich hoffe, ihr hattet Spaß und habt etwas gelernt. Und denkt daran: Statistik muss nicht langweilig sein! Sie kann sogar richtig aufregend sein – fast so aufregend wie ein perfekt ausbalanciertes Glücksrad!