Distribution Function And Density Function
Also, stellt euch vor, ihr sitzt im Café. Latte Macchiato in der Hand, und euer Kumpel fragt plötzlich: "Ey, was ist eigentlich der Unterschied zwischen Verteilungsfunktion und Dichtefunktion? Klingt beides nach Statistik-Folter!" Keine Panik, Freunde. Ich erklär's euch, ohne dass ihr einschlaft.
Die Verteilungsfunktion: Der neugierige Statistik-Detektiv
Die Verteilungsfunktion, oder auf schlau CDF (Cumulative Distribution Function), ist wie ein super-neugieriger Detektiv. Sie will alles über eine Zufallsvariable wissen. "Wie wahrscheinlich ist es, dass X kleiner oder gleich einem bestimmten Wert ist?" Das ist ihre Lieblingsfrage. Stell dir vor, X ist die Wartezeit auf deinen Latte Macchiato. Die Verteilungsfunktion sagt dir dann: "Mit 70% Wahrscheinlichkeit wartest du höchstens 5 Minuten."
Sie ist sozusagen die Summe aller Wahrscheinlichkeiten bis zu einem bestimmten Punkt. Und das Tolle ist: Sie ist immer zwischen 0 und 1. Logisch, denn Wahrscheinlichkeiten können ja nicht negativ sein oder über 100% liegen. Wäre ja auch doof, wenn der Kellner sagt: "Mit 150% Wahrscheinlichkeit kommt Ihr Kaffee gleich!"
Denkt dran: Die Verteilungsfunktion steigt immer an, oder bleibt zumindest gleich. Sie kann nie sinken. Warum? Weil die Wahrscheinlichkeit, dass X kleiner oder gleich einem *höheren* Wert ist, ja nicht kleiner werden kann! Das wäre so, als ob die Anzahl der Leute im Café plötzlich weniger wird, obwohl niemand rausgeht.
Die Dichtefunktion: Der geschwätzige Wahrscheinlichkeits-Papagei
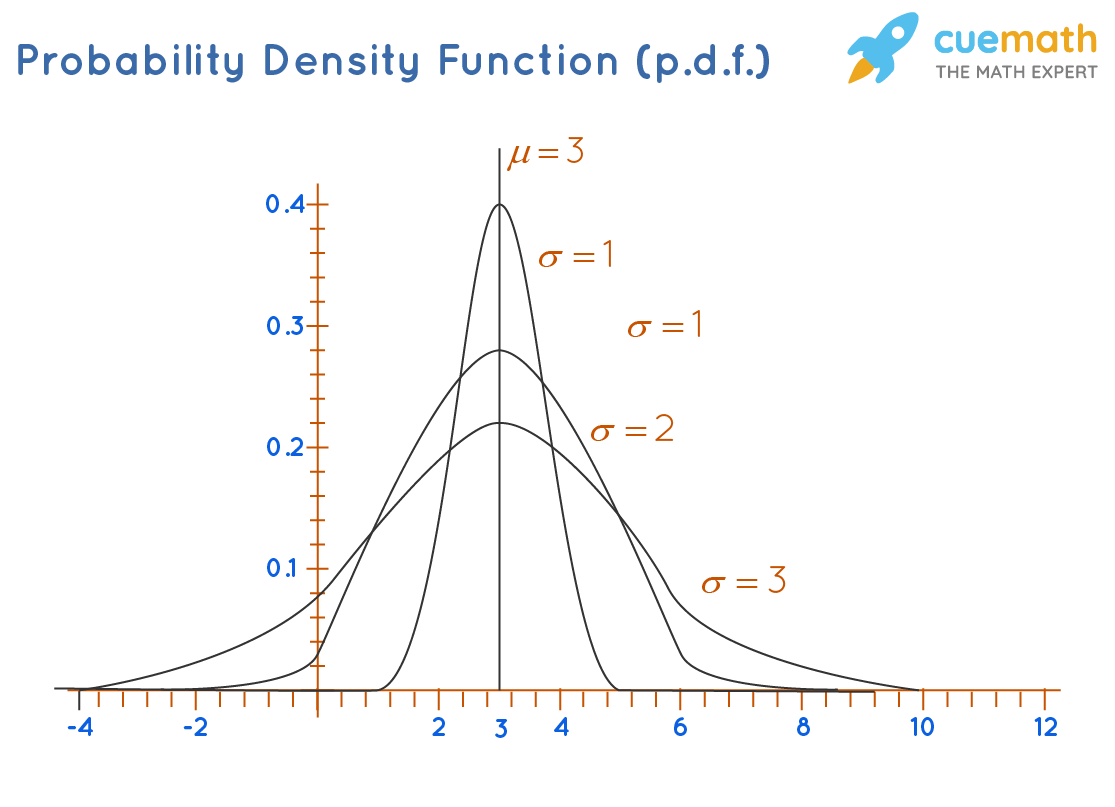
Jetzt kommt die Dichtefunktion, auch bekannt als PDF (Probability Density Function). Sie ist etwas…anders. Sagen wir mal, sie ist der geschwätzige Papagei der Wahrscheinlichkeitsrechnung. Sie "plappert" über die Wahrscheinlichkeitsdichte an jedem einzelnen Punkt. Das bedeutet, sie sagt uns, wie "dicht" die Wahrscheinlichkeit um einen bestimmten Wert herum ist.
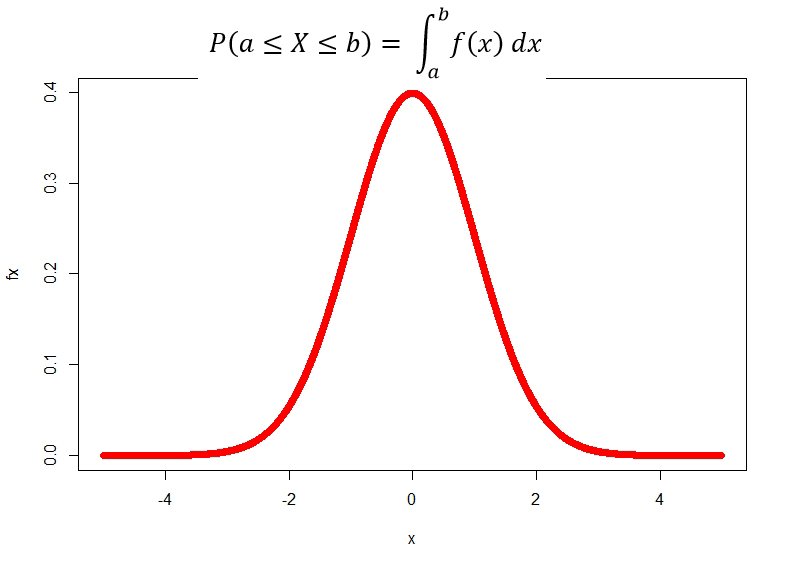
Wichtig: Die Dichtefunktion ist keine Wahrscheinlichkeit! Merkt euch das gut! Sie gibt nur an, wie wahrscheinlich es ist, dass die Zufallsvariable *in der Nähe* eines bestimmten Wertes liegt. Um eine Wahrscheinlichkeit zu bekommen, müsst ihr über einen *Bereich* integrieren (ja, ich weiß, Integration… klingt nach Steuererklärung, ist aber hier ganz harmlos).
Denkt an das Beispiel mit dem Latte Macchiato. Die Dichtefunktion könnte sagen: "Die Wartezeit um genau 3 Minuten hat eine hohe Dichte." Das heißt aber nicht, dass die Wahrscheinlichkeit, *genau* 3 Minuten zu warten, hoch ist. Sondern, dass es wahrscheinlich ist, dass du *ungefähr* 3 Minuten wartest (vielleicht 2.9 Minuten oder 3.1 Minuten).
Ein weiterer wichtiger Unterschied: Die Dichtefunktion kann jeden Wert annehmen, sogar größer als 1! Das ist kein Problem, weil sie ja keine Wahrscheinlichkeit ist. Nur die Fläche unter der gesamten Kurve muss 1 ergeben (100% Wahrscheinlichkeit).
Der Zusammenhang: Ein unzertrennliches Duo
Die Verteilungsfunktion und die Dichtefunktion sind wie Batman und Robin, oder Dick und Doof - sie ergänzen sich perfekt. Die Dichtefunktion ist die Ableitung der Verteilungsfunktion (Achtung, Mathe-Alarm!). Und umgekehrt: Die Verteilungsfunktion ist das Integral der Dichtefunktion. Das bedeutet, wenn du eine von beiden kennst, kannst du die andere berechnen!
Stellt euch vor, die Dichtefunktion ist ein Geschwindigkeitsprofil eines Autos. Die Verteilungsfunktion wäre dann die zurückgelegte Strecke zu einem bestimmten Zeitpunkt. Wenn ihr die Geschwindigkeit (Dichtefunktion) kennt, könnt ihr die Strecke (Verteilungsfunktion) berechnen.
Wann benutze ich was?
Das ist eine gute Frage! Die Verteilungsfunktion ist nützlich, wenn du wissen willst, wie wahrscheinlich es ist, dass eine Zufallsvariable *kleiner oder gleich* einem bestimmten Wert ist. Zum Beispiel: "Wie wahrscheinlich ist es, dass ich heute weniger als 5 Euro ausgebe?"
Die Dichtefunktion ist hilfreich, um zu verstehen, wie die Wahrscheinlichkeit über verschiedene Werte verteilt ist. Zum Beispiel: "Welche Wartezeit auf meinen Latte Macchiato ist am wahrscheinlichsten?"
Zusammenfassend: Die Verteilungsfunktion ist der Detektiv, der Wahrscheinlichkeiten bis zu einem Punkt aufsummiert. Die Dichtefunktion ist der Papagei, der über die Wahrscheinlichkeitsdichte an jedem Punkt plappert. Und beide sind unzertrennlich und helfen uns, Zufallsvariablen besser zu verstehen. So, jetzt wisst ihr Bescheid! Und jetzt... her mit dem Latte Macchiato!