Flächeninhalt Dreieck Gleichseitig Formel
Hast du dich jemals gefragt, wie viel Stoff du für ein dreieckiges Segel benötigst? Oder wie du den Flächeninhalt eines gleichseitigen Beetstücks im Garten berechnen kannst? Keine Sorge, es ist einfacher als du denkst! Wir tauchen ein in die faszinierende Welt des Flächeninhalts von gleichseitigen Dreiecken. Klingt vielleicht erstmal nach trockenem Matheunterricht, aber es steckt mehr dahinter als man denkt. Versprochen!
Warum sollten wir uns damit beschäftigen? Weil es uns hilft, die Welt um uns herum besser zu verstehen und Probleme zu lösen. Der Flächeninhalt eines Dreiecks, insbesondere eines gleichseitigen, ist ein Grundbaustein der Geometrie und findet Anwendung in vielen Bereichen des Lebens. Es ist wie ein kleines Superwerkzeug im Werkzeugkasten unseres Gehirns.
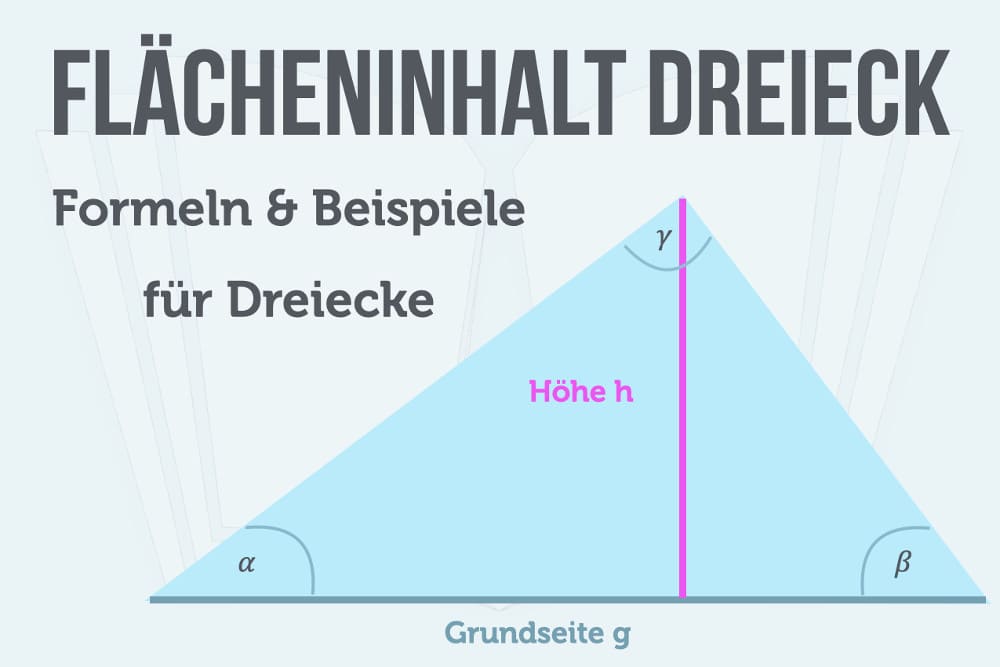
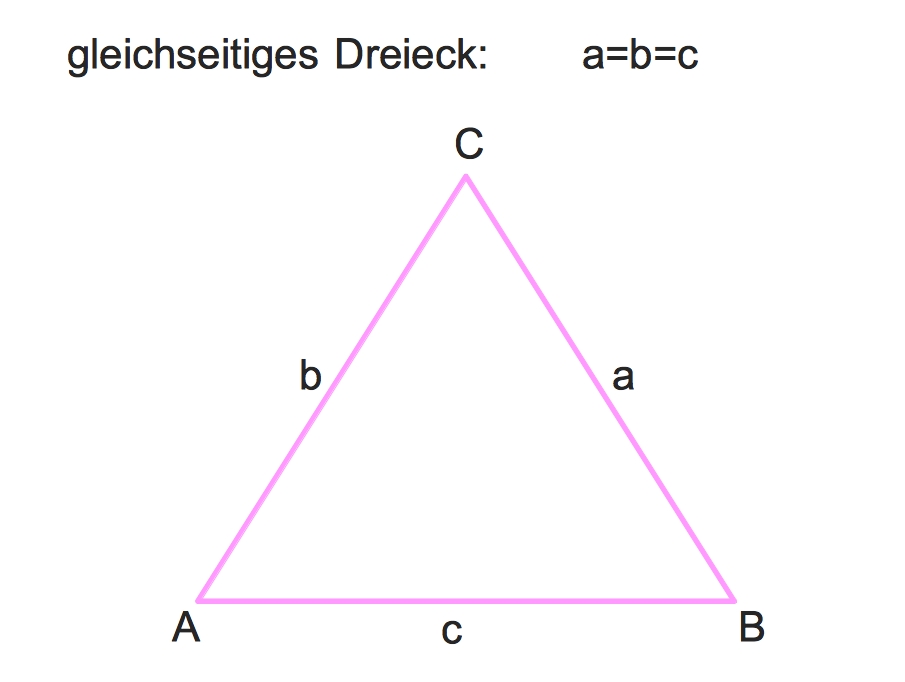
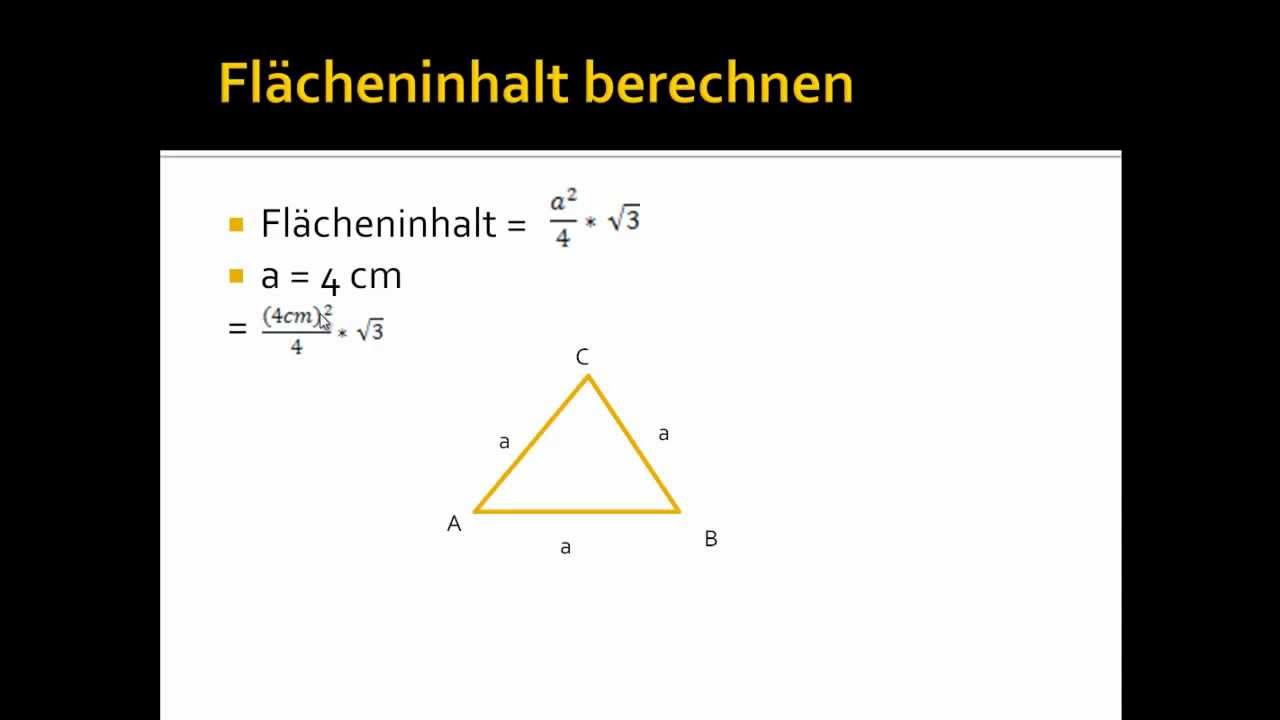
Ein gleichseitiges Dreieck zeichnet sich dadurch aus, dass alle drei Seiten gleich lang sind. Und genau diese Eigenschaft macht die Berechnung des Flächeninhalts besonders elegant. Die Formel lautet: A = (√3 / 4) * a², wobei 'a' die Länge einer Seite ist. Das bedeutet, wir quadrieren einfach die Seitenlänge, multiplizieren sie mit der Quadratwurzel aus 3 und teilen das Ganze durch 4. Klingt kompliziert? Lass uns das aufdröseln!
Der Zweck dieser Formel ist es, uns eine einfache und schnelle Möglichkeit zu geben, den Flächeninhalt zu berechnen, ohne komplizierte Winkelberechnungen durchführen zu müssen. Die Vorteile liegen auf der Hand: Wir sparen Zeit und Mühe und erhalten ein präzises Ergebnis. Stell dir vor, du bist ein Architekt und musst das Dach eines dreieckigen Gebäudes planen. Die Formel für den Flächeninhalt hilft dir, die benötigten Materialien genau zu berechnen und Kosten zu sparen.
Im Unterricht begegnet man dieser Formel meist in der Geometrie. Aufgaben könnten sein: Berechne den Flächeninhalt eines gleichseitigen Dreiecks mit einer Seitenlänge von 5 cm. Oder: Ein gleichseitiges Dreieck hat einen Flächeninhalt von 25√3 cm². Berechne die Seitenlänge. Auch im täglichen Leben finden sich Anwendungen. Wie bereits erwähnt, in der Architektur, aber auch im Handwerk, beim Nähen (Zuschnitt von Stoffen) oder sogar beim Kochen (z.B. bei der Gestaltung von dreieckigen Sandwiches). Stell dir vor, du baust ein Vogelhaus mit einem dreieckigen Dach. Die Flächenberechnung hilft dir, die richtige Größe der Dachplatten zu bestimmen.
Praktische Tipps um diese Formel zu erkunden: Zeichne verschiedene gleichseitige Dreiecke mit unterschiedlichen Seitenlängen. Berechne den Flächeninhalt jedes Dreiecks und vergleiche die Ergebnisse. Nutze ein Geometrieprogramm oder eine App, um die Formel zu visualisieren. Viele Apps bieten interaktive Möglichkeiten, die Seitenlänge zu verändern und den Flächeninhalt direkt anzeigen zu lassen. Das hilft, ein besseres Gefühl für die Zusammenhänge zu bekommen. Du kannst auch versuchen, die Formel herzuleiten, indem du ein gleichseitiges Dreieck in zwei rechtwinklige Dreiecke teilst und den Satz des Pythagoras anwendest. Das ist eine tolle Übung, um dein mathematisches Verständnis zu vertiefen!
Also, keine Angst vor der Formel! Sie ist ein nützliches Werkzeug, das uns hilft, die Welt um uns herum besser zu verstehen. Probiere es aus, spiele damit und entdecke die spannende Welt der Geometrie!