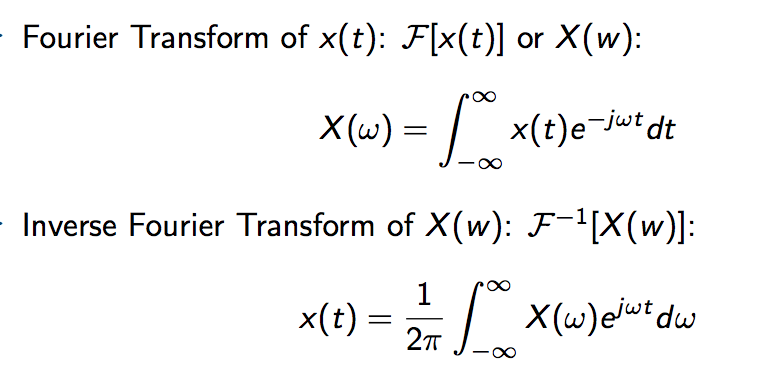Fourier Transform And Inverse Fourier Transform

Hey Leute, habt ihr euch jemals gefragt, wie eure Lieblingsmusik auf Spotify klingt? Oder wie euer Smartphone ein so klares Bild macht, obwohl das Licht ständig flackert? Die Antwort könnte in etwas stecken, das sich Fourier-Transformation nennt! Klingt erstmal kompliziert, oder? Aber keine Sorge, wir brechen das mal runter, ganz entspannt.
Was ist diese Fourier-Transformation überhaupt?
Stellt euch vor, ihr habt einen Smoothie. Ein leckerer Mix aus Erdbeeren, Bananen, Milch und vielleicht noch ein bisschen Spinat (für die Gesundheit, natürlich!). Ihr könnt den Smoothie probieren und wisst, er schmeckt nach all diesen Zutaten, aber ihr seht sie nicht einzeln, richtig?
Die Fourier-Transformation ist so ähnlich. Sie nimmt ein Signal – das kann eine Schallwelle, ein Bild oder sogar Aktienkursverläufe sein – und zerlegt es in seine "Zutaten". Diese "Zutaten" sind im Wesentlichen verschiedene Frequenzen. Jede Frequenz hat ihre eigene Stärke oder "Lautstärke", sozusagen.
Also, statt eines Smoothies, den wir probieren, haben wir ein Signal, das wir analysieren. Und statt Erdbeeren und Bananen haben wir verschiedene Frequenzen, die zusammen das Signal ausmachen. Krass, oder?
Warum ist das jetzt so cool? Nun, stellt euch vor, ihr wisst genau, welche Zutaten in eurem Smoothie sind. Ihr könntet ihn nachbauen oder ihn anpassen, um ihn noch besser zu machen! Genauso können wir Signale manipulieren, nachdem wir sie mit der Fourier-Transformation zerlegt haben.
Von Zeit zu Frequenz und zurück!
Okay, wir wissen jetzt, dass die Fourier-Transformation ein Signal in seine Frequenzkomponenten zerlegt. Aber was bedeutet das konkret?
Nehmen wir mal ein einfaches Beispiel: eine Gitarrensaite. Wenn ihr eine Saite anschlagt, schwingt sie mit einer bestimmten Frequenz. Diese Frequenz bestimmt den Ton, den ihr hört. Die Fourier-Transformation würde diese Frequenz "erkennen" und ihre Stärke (wie laut die Saite klingt) angeben. Aber die meisten Töne sind nicht so einfach; sie bestehen aus vielen Frequenzen gleichzeitig, den sogenannten Obertönen!
Und jetzt kommt der Clou: Es gibt auch eine Inverse Fourier-Transformation! Sie macht genau das Gegenteil. Sie nimmt die Frequenzkomponenten und setzt sie wieder zusammen, um das ursprüngliche Signal zu erzeugen. Das ist wie beim Smoothie: Ihr nehmt die einzelnen Zutaten und mixt sie wieder zusammen, um den ursprünglichen Smoothie zu bekommen!
Man kann sich das wie ein Tor vorstellen: Du gehst durch das "Fourier-Tor" und kommst in die Frequenzwelt. Dann gehst du durch das "Inverse Fourier-Tor" und bist wieder zurück in der Zeitwelt (oder der Bildwelt, oder was auch immer du angefangen hast!).
Wo wird das denn überall verwendet?
Überall! Wirklich! Habt ihr euch jemals gefragt, wie Noise-Cancelling-Kopfhörer funktionieren? Sie analysieren den Umgebungslärm (mit der Fourier-Transformation) und erzeugen dann ein Gegensignal (mit der Inversen Fourier-Transformation), um den Lärm auszulöschen. Genial, oder?
Oder denkt an Bildbearbeitungsprogramme. Mit der Fourier-Transformation können wir bestimmte Frequenzen in einem Bild verstärken oder abschwächen. Das ist super nützlich, um Bilder zu schärfen oder Rauschen zu entfernen.
Und was ist mit der Medizin? Die MRT (Magnetresonanztomographie) verwendet die Fourier-Transformation, um Bilder vom Inneren unseres Körpers zu erzeugen! Die Analyse von EEG-Signalen (Elektroenzephalogramm) zur Erkennung von Gehirnaktivitäten beruht ebenfalls darauf. Verrückt, was?
Die Telekommunikation wäre ohne die Fourier-Transformation undenkbar. Sie ermöglicht es uns, Daten effizient zu komprimieren und zu übertragen. Euer WLAN-Router verdankt sein Funktionieren im Grunde auch dieser genialen mathematischen Transformation.
Also, was lernen wir daraus?
Die Fourier-Transformation und ihre inverse Schwester sind unglaublich mächtige Werkzeuge, die in vielen Bereichen unseres Lebens eine Rolle spielen, oft ohne dass wir es überhaupt merken. Sie ermöglichen es uns, Signale zu analysieren, zu manipulieren und zu verstehen, wie die Welt um uns herum funktioniert. Und das ist doch ziemlich cool, oder?
Das nächste Mal, wenn ihr eure Lieblingsmusik hört, ein Foto bearbeitet oder ein medizinisches Bild betrachtet, denkt daran: Im Hintergrund werkelt vielleicht gerade die Fourier-Transformation!