Funktionsgleichung Mit 2 Punkten Bestimmen

Hey du Mathe-Muffel (oder vielleicht auch Mathe-Held?), lass uns mal über Funktionsgleichungen reden. Keine Panik, wird nicht trocken! Stell dir vor, wir wollen das Rezept für eine lineare Funktion herausfinden, aber wir haben nur zwei Zutaten: zwei Punkte. Klingt wie eine Mathe-Krimi, oder?
Also, was brauchen wir, um eine Funktionsgleichung zu bestimmen? Nun, für eine lineare Funktion (also eine schnurgerade Linie) ist das Rezept ganz einfach: y = mx + b. "m" ist die Steigung (wie steil die Linie geht) und "b" ist der y-Achsenabschnitt (wo die Linie die y-Achse schneidet). Klingt kompliziert? Keine Sorge, wir kochen das runter!
Schritt 1: Die Steigung – Bergziegen-Mathematik
Die Steigung "m" ist sozusagen der schwierigste Teil, aber keine Angst, wir kriegen das hin! Denk an eine Bergziege, die einen Hang hochklettert. Die Steigung sagt uns, wie viel die Ziege nach oben klettert (Änderung in y), für jeden Schritt, den sie zur Seite macht (Änderung in x). Mathematisch ausgedrückt:
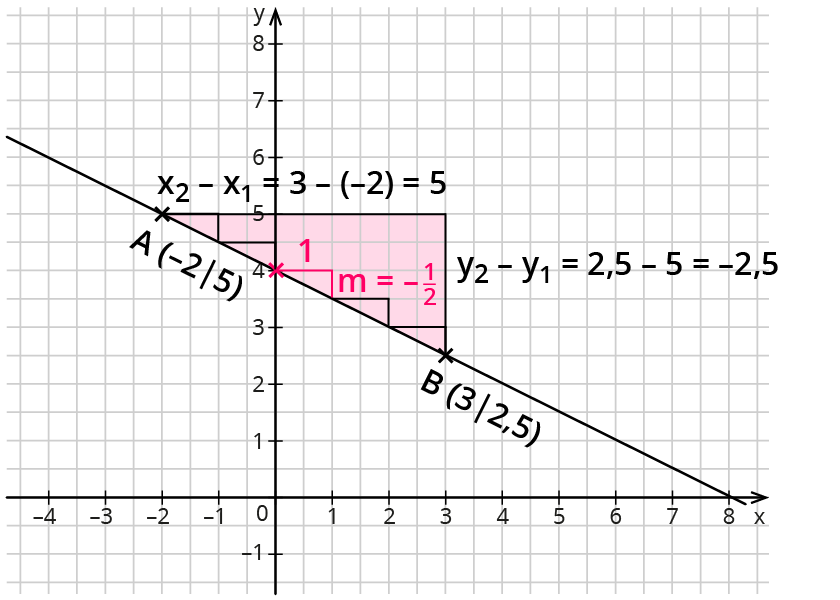
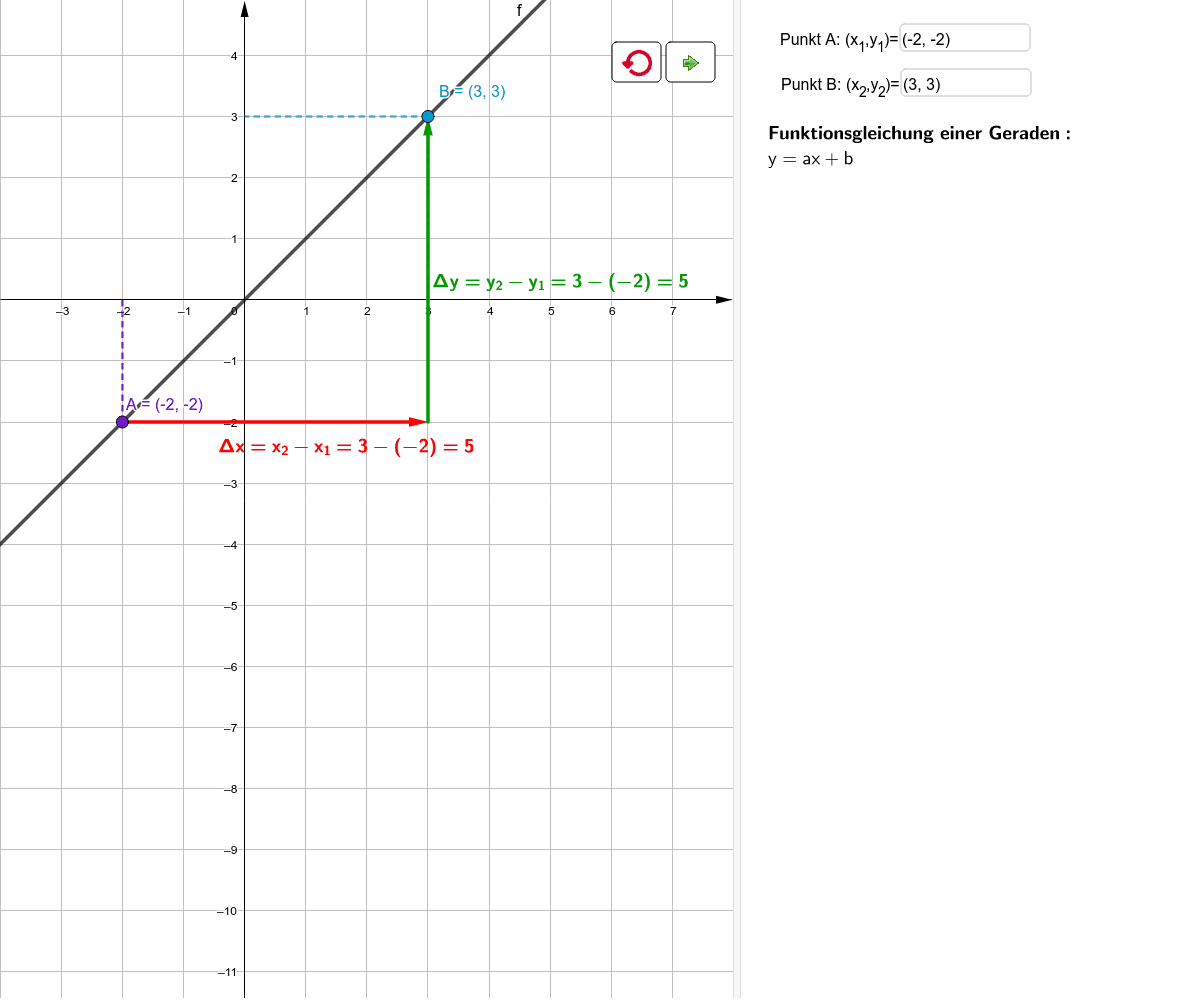
m = (y2 - y1) / (x2 - x1)
Hä? Okay, anders formuliert: Du hast zwei Punkte (x1, y1) und (x2, y2). Du ziehst einfach die y-Werte voneinander ab und teilst das Ergebnis durch die Differenz der x-Werte. Wichtig: Achte darauf, dass du die Reihenfolge beibehältst! Nicht, dass du am Ende eine Bergziege hast, die rückwärts den Berg runterpurzelt (das wäre schlecht für die Mathe-Note).
Beispiel: Punkt A (1, 3) und Punkt B (4, 9). Also:
m = (9 - 3) / (4 - 1) = 6 / 3 = 2
Die Steigung ist 2. Unsere Bergziege ist also ganz schön fleißig!
Schritt 2: Der y-Achsenabschnitt – Wo die Linie chillt
Jetzt kommt der einfache Teil! Wir haben die Steigung "m" und wir haben immer noch unsere zwei Punkte. Wir nehmen einen dieser Punkte (ist egal welchen, beide funktionieren – ist wie Magie!) und setzen ihn zusammen mit der Steigung in unsere Grundgleichung y = mx + b ein. Und dann lösen wir nach "b" auf.
Nehmen wir Punkt A (1, 3) und unsere Steigung m = 2. Dann:
3 = 2 * 1 + b
3 = 2 + b
b = 1
Der y-Achsenabschnitt ist 1. Das heißt, unsere Linie schneidet die y-Achse bei y = 1. Sie chillt da gemütlich!
Schritt 3: Das fertige Rezept – Voilà!
Jetzt haben wir alle Zutaten! Wir setzen unsere Steigung (m = 2) und unseren y-Achsenabschnitt (b = 1) in unsere Grundgleichung ein:
y = 2x + 1
Tada! Das ist die Funktionsgleichung der Linie, die durch die Punkte A (1, 3) und B (4, 9) verläuft. Du hast es geschafft! Du bist ein Mathe-Koch!
Kleiner Tipp: Wenn du dir unsicher bist, ob du richtig gerechnet hast, kannst du den anderen Punkt (B) auch noch in die Gleichung einsetzen. Wenn die Gleichung stimmt, dann hast du alles richtig gemacht!
Was, wenn die Punkte doof sind?
Manchmal geben dir die Mathe-Götter aber auch Punkte, die nicht so schön glatt sind. Mit Kommazahlen und Brüchen. Keine Panik! Die Methode ist genau die gleiche. Einfach einsetzen und rechnen. Kann zwar etwas mehr Aufwand sein, aber das Ergebnis ist das Gleiche.
Und jetzt?
Jetzt geh raus und bestimme Funktionsgleichungen! Nimm dir zwei zufällige Punkte und übe. Je öfter du das machst, desto einfacher wird es. Und denk dran: Mathe ist wie ein Muskel. Je mehr du ihn trainierst, desto stärker wird er.
Also, Kopf hoch, Stift gezückt und los geht's! Du rockst das!