Lagebeziehung Zwischen Gerade Und Ebene
Okay, Leute, stellt euch vor: Eine Gerade und eine Ebene treffen sich in einer Bar. Klingt nach dem Anfang eines schlechten Witzes? Ist es auch, aber es geht um Mathematik! Und Mathe *kann* lustig sein, versprochen! Wir reden über die Lagebeziehung zwischen Gerade und Ebene. Ja, das klingt furchtbar kompliziert, aber keine Panik, wir zerlegen das in mundgerechte Stücke, versprochen.
Die drei Musketiere (der Lagemöglichkeiten)
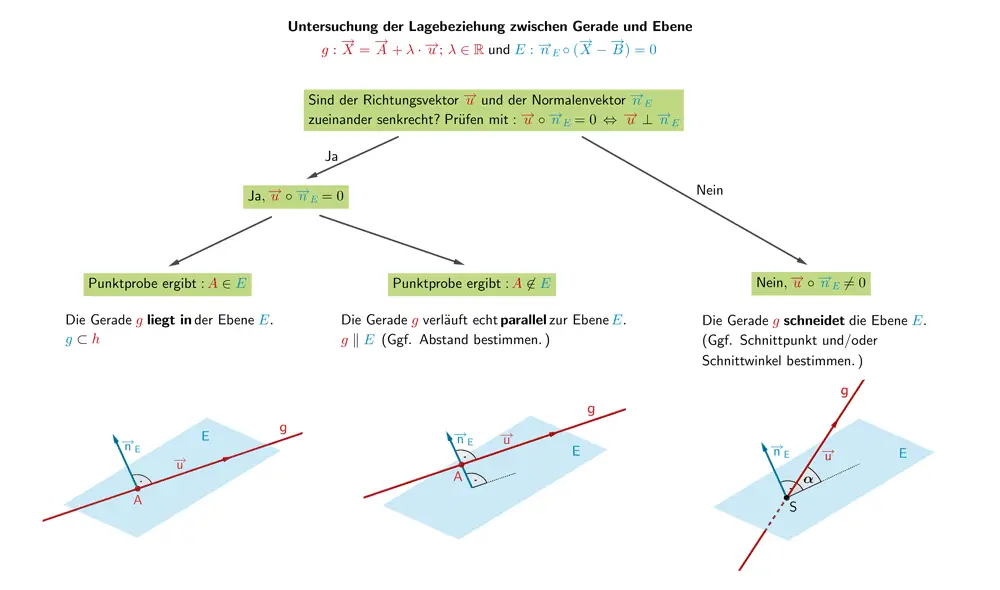
Es gibt im Grunde nur drei Möglichkeiten, wie eine Gerade und eine Ebene miteinander interagieren können. Nennt sie ruhig die drei Musketiere der geometrischen Beziehungen: Einer für alle, alle für… naja, für die Lage der Gerade zur Ebene! Hier sind sie, in ihrer ganzen Pracht:
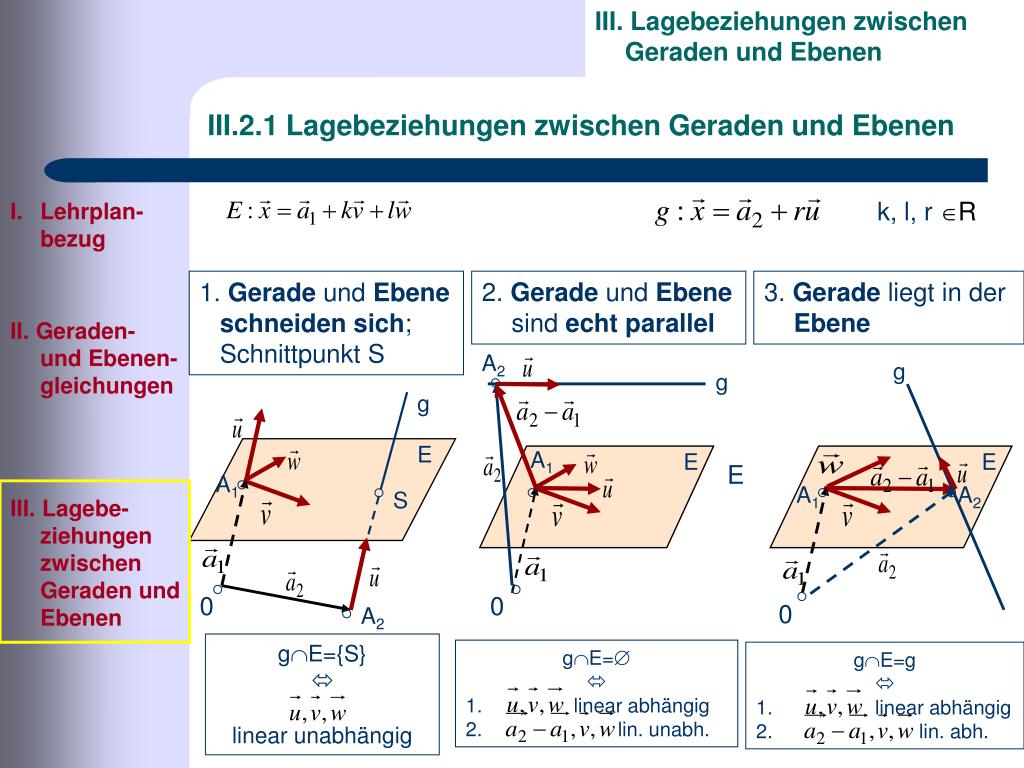
- Die Gerade liegt *in* der Ebene. Stellt euch vor, die Gerade ist ein fauler Wurm, der es sich in einer riesigen Pfannkuchen-Ebene gemütlich macht. Sie ist Teil der Ebene, eine Art eingebautes Extra. Keine Aufregung, alles friedlich.
- Die Gerade schneidet die Ebene. Boom! Hier wird's interessant! Die Gerade rammt die Ebene wie ein Speer. Es gibt einen Schnittpunkt, einen heiligen Ort, wo sich die beiden treffen. Denkt an ein Schwert, das durch einen Kuchen geht. Mmmm, Kuchen!
- Die Gerade ist parallel zur Ebene. Die Gerade und die Ebene sind wie zwei schüchterne Teenager auf einer Party: Sie sehen sich, aber trauen sich nicht, miteinander zu reden. Sie verlaufen nebeneinander, ohne sich jemals zu berühren. Eine traurige, parallel verlaufende Romanze.
Also, das ist es im Großen und Ganzen. Aber wie finden wir heraus, welche dieser Beziehungen gerade im Spiel ist? Keine Sorge, wir haben Tools! (Okay, es sind mathematische Gleichungen, aber "Tools" klingt cooler, oder?)
Die Detektivarbeit: Gleichungen und Vektoren
Jetzt wird's ein bisschen technischer, aber keine Angst, ich verspreche, es bleibt relativ schmerzfrei. Wir brauchen Gleichungen! Jede Gerade und jede Ebene lässt sich durch eine Gleichung beschreiben. Stellt euch vor, es sind ihre Tinder-Profile in mathematischer Form!
Die Ebene hat meistens eine Normalenform. Das ist wie eine Art "Fingerabdruck" der Ebene, der senkrecht auf ihr steht. Dieser Fingerabdruck hilft uns zu erkennen, wie die Gerade zur Ebene positioniert ist. Wir brauchen auch einen Richtungsvektor für die Gerade. Der zeigt, wohin die Gerade "zeigt", in welche Richtung sie sich bewegt. Denk an ihn als ihren persönlichen Kompass.
Der Trick ist jetzt, das Skalarprodukt (auch bekannt als Punktprodukt) zwischen dem Normalenvektor der Ebene und dem Richtungsvektor der Gerade zu berechnen. Was ist das Skalarprodukt? Nun, es ist eine magische mathematische Operation, die uns verrät, wie "gleichgerichtet" zwei Vektoren sind. Keine Sorge, ihr müsst es nicht selbst berechnen! Lasst das eure Taschenrechner oder Mathe-Apps erledigen. Die sind dafür da!
Was uns dieses Skalarprodukt verrät, ist entscheidend:
- Skalarprodukt = 0: Dann sind der Normalenvektor und der Richtungsvektor senkrecht zueinander. Das bedeutet, die Gerade ist entweder parallel zur Ebene oder sie liegt in der Ebene. Um das zu unterscheiden, setzen wir einfach einen Punkt der Gerade in die Ebenengleichung ein. Wenn die Gleichung stimmt, liegt die Gerade in der Ebene! Ansonsten sind sie parallel.
- Skalarprodukt ≠ 0: Juhu! Die Gerade schneidet die Ebene! Um den Schnittpunkt zu finden, müssen wir ein kleines Gleichungssystem lösen. Aber keine Panik, das ist wie ein kleines Puzzle, kein Weltuntergang.
Praktische Anwendung: Wo ist das eigentlich wichtig?
Okay, ich weiß, ihr denkt jetzt vielleicht: "Das ist ja alles schön und gut, aber wann brauche ich das im echten Leben?" Überraschend oft! Denkt an:
- Computergrafik: Um zu bestimmen, wie Licht auf Oberflächen fällt oder um Kollisionen zu vermeiden.
- Robotik: Um Roboter durch den Raum zu navigieren.
- Architektur: Um sicherzustellen, dass Gebäude stabil sind und nicht einfach umfallen. (Sehr wichtig!)
- Fluglotsen: (Okay, nicht direkt, aber die Mathematik dahinter ist ähnlich, um Flugrouten zu planen und Kollisionen zu vermeiden)
Also, das nächste Mal, wenn ihr einen perfekt animierten Film seht, einen Roboter herumwuseln seht oder ein wunderschönes Gebäude bewundert, denkt daran: Dahinter steckt wahrscheinlich die Lagebeziehung zwischen Gerade und Ebene! Und vielleicht auch ein bisschen Mathe-Magie.
Fazit: Mathe ist gar nicht so schlimm (manchmal)
Die Lagebeziehung zwischen Gerade und Ebene mag am Anfang etwas einschüchternd wirken, aber wenn man sie in ihre Einzelteile zerlegt, ist sie eigentlich gar nicht so schlimm. Und wer weiß, vielleicht habt ihr ja sogar Spaß dabei! (Okay, vielleicht nicht *so* viel Spaß, aber zumindest ein bisschen weniger Angst vor Mathe.) Also, geht raus und erobert die geometrische Welt! Und denkt daran: Parallel verlaufende Geraden müssen nicht immer traurig sein. Sie können auch einfach nur… parallel sein. Ist doch auch okay, oder?