Lineare Gleichungssysteme Grafisch Lösen Aufgaben Pdf
Hey du! Mal wieder am Verzweifeln wegen Mathe? Keine Panik, ich kenn das Gefühl. Heute quatschen wir mal ganz entspannt über lineare Gleichungssysteme und wie man die grafisch löst. Klingt erstmal nach totalem Horror, ich weiß, aber versprochen, es wird einfacher als du denkst! Und wir reden über diese ominösen Aufgaben im PDF-Format, die einen immer so anstarren...
Was sind lineare Gleichungssysteme überhaupt?
Okay, ganz kurz die Basics. Stell dir vor, du hast zwei (oder mehr) Gleichungen mit zwei (oder mehr) Variablen. Zum Beispiel sowas wie: x + y = 5 und x - y = 1. Das Ziel? Die Werte für x und y finden, die beide Gleichungen gleichzeitig erfüllen. Also, quasi die Lösung für beide "Rätsel" gleichzeitig. Klingt doch logisch, oder? (Oder zumindest halbwegs logisch?)
Grafisch lösen – Wie geht das denn?
Jetzt kommt der spaßige Teil! Anstatt komplizierte Rechnungen anzustellen, zeichnen wir einfach! Jede lineare Gleichung lässt sich als Gerade in einem Koordinatensystem darstellen. Denkst du jetzt: "Koordinatensystem? Oh nein!"? Keine Sorge, das ist einfacher als es klingt. Einfach ein Kreuz mit x- und y-Achse. Tada!
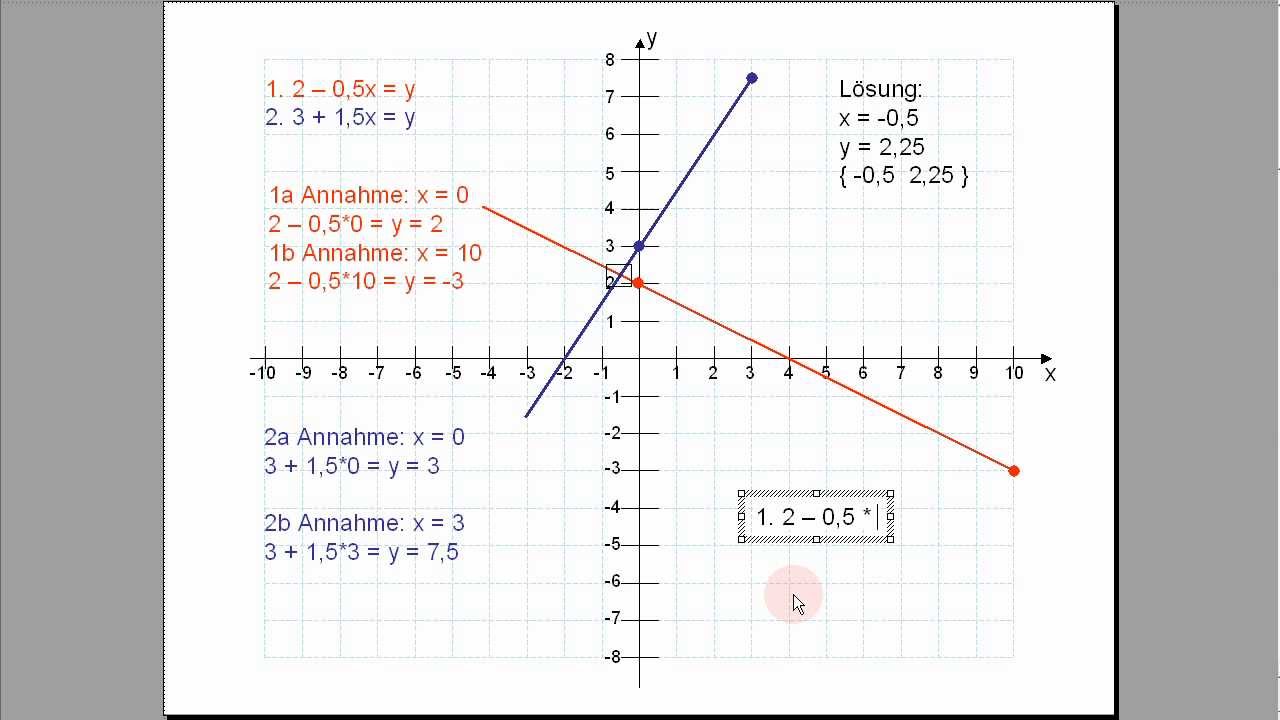
Um die Gerade zu zeichnen, brauchst du mindestens zwei Punkte. Setz einfach zwei verschiedene x-Werte in die Gleichung ein und berechne das zugehörige y. Diese beiden Punkte verbindest du mit einer Linie – fertig ist die Gerade! Und das machst du für jede Gleichung in deinem System. Ist ja fast schon Kunst, oder?
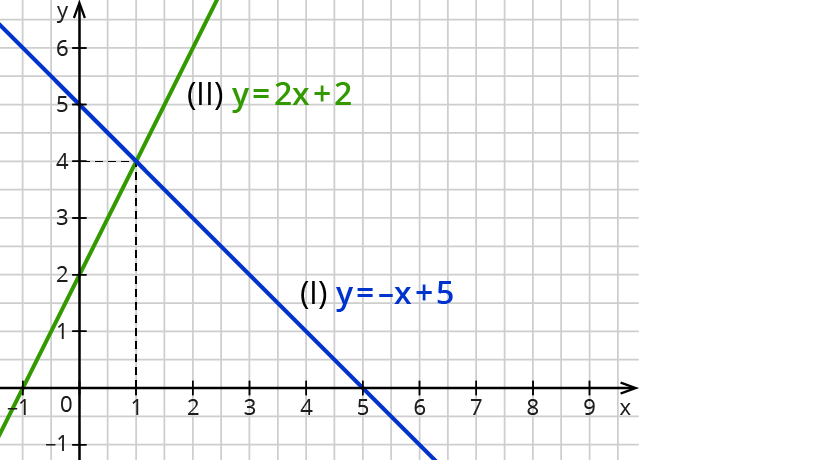
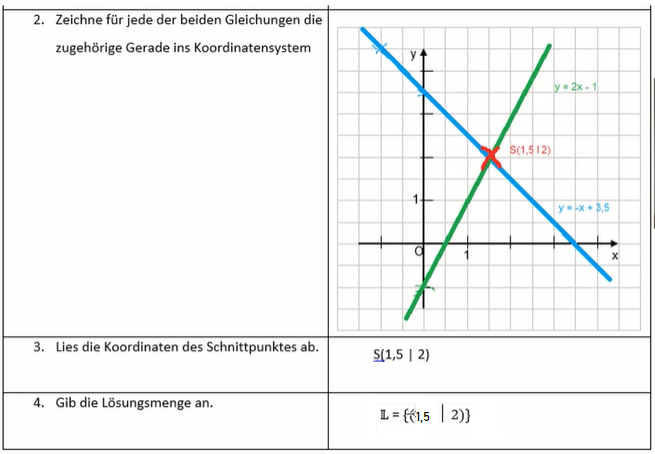
Der Clou: Der Schnittpunkt der beiden Geraden (falls es einen gibt!) ist die Lösung deines linearen Gleichungssystems! Die x- und y-Koordinaten des Schnittpunkts sind die Werte, die beide Gleichungen erfüllen. Genial, oder? Quasi Mathe mit Malen nach Zahlen!
Diese verdammten Aufgaben-PDFs!
Jetzt zu den PDFs. Du kennst das: Du öffnest das Ding, und da sind 10 Aufgaben, die alle gleich aussehen. Der Trick? Ruhig bleiben und eine Aufgabe nach der anderen angehen. Wichtig: Achte genau auf die Vorzeichen! Ein kleines Minus zu viel oder zu wenig kann alles ruinieren. (Ich spreche da aus Erfahrung...hust...)
Wenn du die Gleichungen in den Aufgaben-PDFs grafisch lösen sollst, empfehle ich dir, dir ein ordentliches Blatt Papier zu schnappen (oder ein Grafikprogramm auf dem Computer zu nutzen, falls du's digital magst). Zeichne das Koordinatensystem sauber ein und achte darauf, dass die Skala stimmt. Sonst wird das mit dem Ablesen des Schnittpunkts nämlich schwierig.
Tipps und Tricks für's grafische Lösen
- Sauberkeit ist Trumpf! Eine unsaubere Zeichnung führt zu ungenauen Ergebnissen. Und wer will das schon?
- Wähle einfache Zahlen! Wenn du die Punkte für die Geraden berechnest, nimm am besten kleine, ganze Zahlen für x. Das macht das Rechnen einfacher.
- Prüfe deine Lösung! Setze die x- und y-Werte, die du am Schnittpunkt abgelesen hast, in beide ursprünglichen Gleichungen ein. Stimmt es? Super! Stimmt es nicht? Dann hast du dich irgendwo verrechnet oder ungenau gezeichnet. Nochmal versuchen!
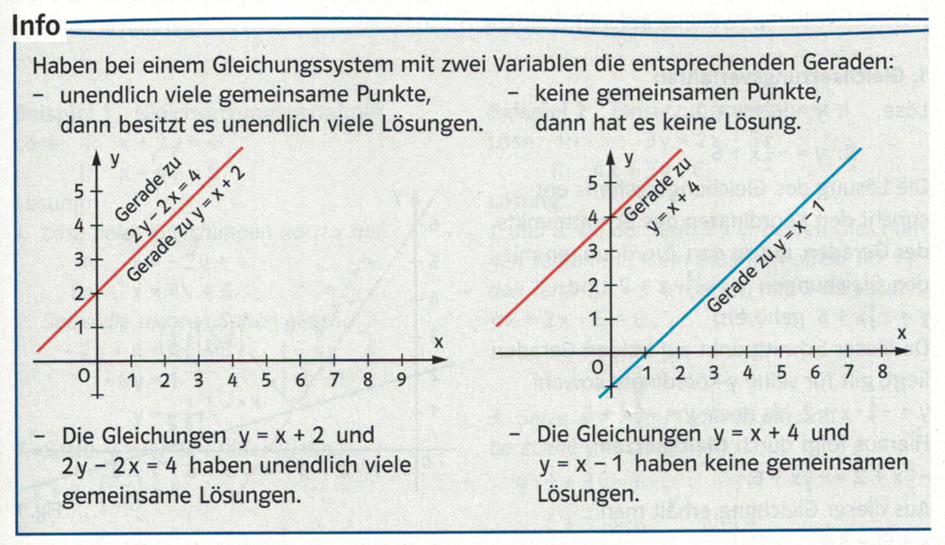
- Was, wenn sich die Geraden nicht schneiden? Wenn die Geraden parallel verlaufen, gibt es keine Lösung! Die Gleichungen sind widersprüchlich. Und wenn die Geraden aufeinanderliegen? Dann gibt es unendlich viele Lösungen!
Achte auf Spezialfälle! Manchmal sind die Gleichungen in den Aufgaben-PDFs etwas "versteckt". Vielleicht musst du sie erst umformen, bevor du sie grafisch darstellen kannst. Lass dich nicht verunsichern! Ein bisschen Algebra-Gymnastik schadet nie! Denk dran: Ziel ist es, die Gleichung in die Form y = mx + b zu bringen (m = Steigung, b = y-Achsenabschnitt). Das macht das Zeichnen zum Kinderspiel!
Und jetzt? Ab ans Werk!
So, genug gequatscht! Jetzt bist du dran. Schnapp dir ein Aufgaben-PDF (oder such dir eins im Internet) und probier's einfach aus. Am Anfang ist es vielleicht etwas knifflig, aber mit etwas Übung wirst du zum Profi im grafischen Lösen von linearen Gleichungssystemen. Und denk dran: Wenn du mal nicht weiterweißt, frag einfach! Es gibt genug Leute, die dir gerne helfen (mich zum Beispiel! Zumindest, wenn ich gerade nicht selbst über Mathe brüte...). Viel Erfolg!