Lineare Gleichungssysteme Mit 3 Unbekannten
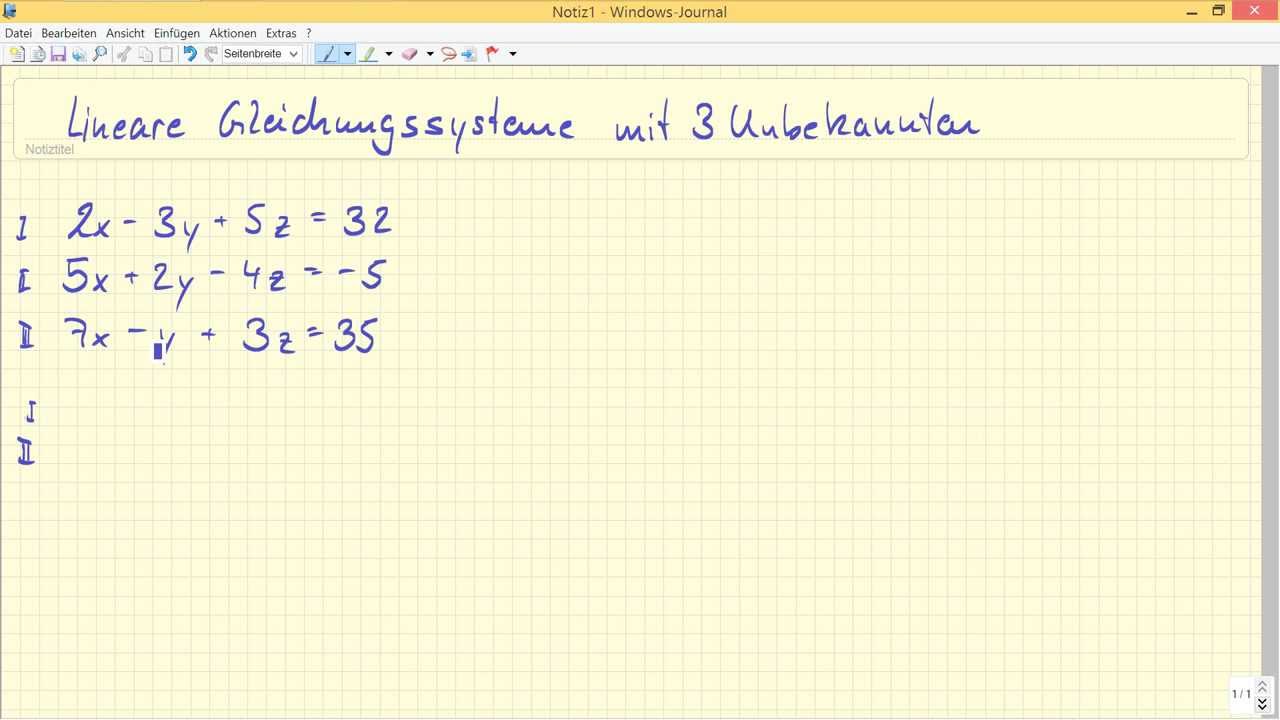
Stell dir vor, du bist Detektiv! Nicht irgendein Detektiv, sondern der beste Detektiv aller Zeiten! Dein Fall: Das große Kuchenrätsel! Es gibt drei Verdächtige: Anna, Ben und Clara. Jeder von ihnen hat heimlich Kuchen gegessen. Deine Aufgabe: Herauszufinden, wie viele Stücke jeder von ihnen verdrückt hat!
Die Spurensuche beginnt!
Du findest drei wichtige Hinweise, drei kryptische Botschaften, die eigentlich lineare Gleichungssysteme mit 3 Unbekannten sind. Klingt kompliziert? Keine Panik! Es ist einfacher als du denkst, versprochen! Stell dir jede Person (Anna, Ben, Clara) als eine unbekannte Variable vor: nennen wir sie A, B und C.
Hier sind deine Hinweise, übersetzt in Detektivsprache:
Hinweis 1: Anna hat doppelt so viele Stücke gegessen wie Ben. (A = 2B)
Hinweis 2: Zusammen haben alle drei 10 Stücke Kuchen verputzt. (A + B + C = 10)
Hinweis 3: Clara hat ein Stück weniger gegessen als Ben. (C = B - 1)
Das sind deine drei Gleichungen! Sie bilden ein lineares Gleichungssystem. Und das bedeutet, wir können mit etwas Knobelei herausfinden, wer wie viele Stücke Kuchen gegessen hat!
Die Lösungsmethoden: Dein Detektiv-Werkzeugkasten
Es gibt verschiedene Methoden, um solche Rätsel zu lösen. Stell sie dir vor wie Spezialwerkzeuge in deinem Detektiv-Werkzeugkasten:
- Einsetzungsverfahren: Dein Lieblingswerkzeug, um Verdächtige zu überführen! Du nimmst eine Gleichung, in der eine Variable schon fast entlarvt ist (wie A = 2B) und setzt sie in eine andere Gleichung ein. So reduzierst du die Anzahl der Unbekannten!
- Gleichsetzungsverfahren: Wenn zwei Gleichungen den gleichen Wert auf einer Seite haben, kannst du die andere Seite einfach gleichsetzen! Perfekt, um widersprüchliche Aussagen zu entlarven!
- Additions-/Subtraktionsverfahren: Manchmal musst du Gleichungen addieren oder subtrahieren, um eine Variable loszuwerden. Denk daran wie beim Schach – ein strategischer Zug, um deinen Gegner (die unbekannte Variable) auszuschalten!
Für unser Kuchenrätsel eignet sich das Einsetzungsverfahren super. Wir wissen: A = 2B und C = B - 1. Also setzen wir das in die zweite Gleichung ein (A + B + C = 10):
2B + B + (B - 1) = 10
Jetzt haben wir nur noch die Variable B! Das können wir lösen:
4B - 1 = 10
4B = 11
B = 2.75
Moment mal! 2,75 Kuchenstücke? Das geht ja gar nicht! Kuchenstücke sind immer ganze Zahlen! Hier kommt die Realität ins Spiel. Vielleicht haben wir einen Fehler gemacht, oder vielleicht hat jemand gelogen (Kuchen-Lügner!).
Nehmen wir an, die Hinweise sind leicht vereinfacht. Sagen wir, Ben hat 3 Stücke gegessen. Dann wäre:
A = 2 * 3 = 6
C = 3 - 1 = 2
A + B + C = 6 + 3 + 2 = 11
Fast! Vielleicht war der Hinweis 2 etwas ungenau. Sagen wir, es waren insgesamt 11 Stück Kuchen. Dann haben wir unseren Täter!
Der Fall ist gelöst (fast)!
Also: Anna hat 6 Stücke gegessen, Ben 3 und Clara 2. Das Kuchenrätsel ist geknackt! Du bist ein genialer Detektiv!
Wichtig: In der echten Welt können lineare Gleichungssysteme auch Lösungen haben, die keine ganzen Zahlen sind. Aber bei Kuchen wollen wir es doch realistisch, oder?
Das Ganze mag anfangs etwas einschüchternd wirken, aber mit etwas Übung und der richtigen Einstellung wirst du zum Meister der linearen Gleichungssysteme! Und wer weiß, vielleicht löst du damit bald nicht nur Kuchenrätsel, sondern auch die kompliziertesten Probleme der Welt!
Denk daran: Mathe ist wie Detektivarbeit – spannend, herausfordernd und unglaublich befriedigend, wenn man den Fall gelöst hat!




