Logistische Regression Interpretation Spss

Hey, du Statistik-Superheld! Lass uns heute mal über Logistische Regression in SPSS quatschen. Keine Angst, das klingt schlimmer, als es ist. Stell dir vor, du bist ein Detektiv, der herausfinden will, warum manche Leute Pizza mit Ananas lieben (ich weiß, schockierend!) und andere nicht. Die Logistische Regression hilft dir dabei, die versteckten Hinweise zu finden.

Was zum Kuckuck ist Logistische Regression überhaupt?

Okay, ganz einfach: Die Logistische Regression ist wie eine normale Regression, nur dass sie nicht versucht, eine *kontinuierliche* Variable (wie z.B. Körpergröße) vorherzusagen, sondern eine *kategorische* (wie "mag Pizza mit Ananas" vs. "mag keine Pizza mit Ananas"). Denk an Ja/Nein, 0/1, oder eben Pizza-Vorliebe. Sie sagt dir, wie wahrscheinlich es ist, dass jemand zu einer bestimmten Kategorie gehört, basierend auf anderen Variablen.

Stell dir vor, du willst wissen, ob das Alter und die Anzahl der abonnierten Kochzeitschriften beeinflussen, ob jemand ein Sternekoch wird. Die Logistische Regression kann dir dabei helfen! (Auch wenn ich vermute, dass Talent und Leidenschaft da auch eine Rolle spielen... nur so nebenbei).

SPSS, mein bester Freund (oder so ähnlich)

SPSS ist dein Werkzeugkasten. Hier kannst du die ganze Magie passieren lassen. Keine Sorge, du musst kein Zauberer sein. Die Menüs sind relativ einfach zu bedienen (okay, manchmal sind sie ein bisschen versteckt, aber wir finden sie schon!).

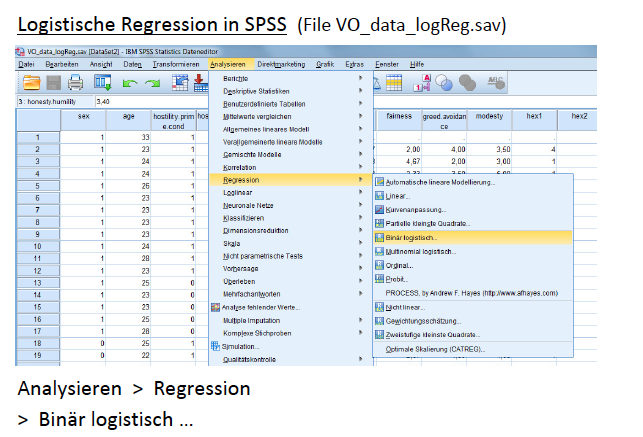
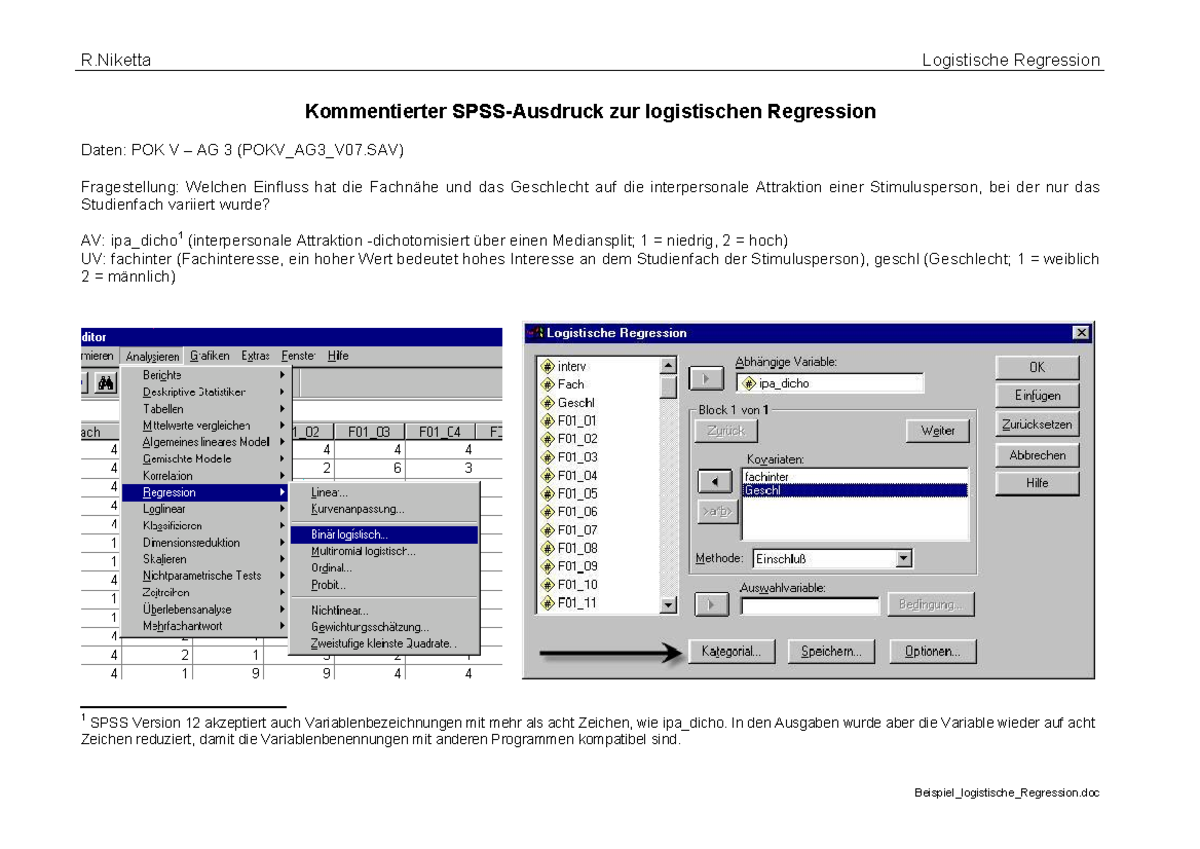
Um eine Logistische Regression in SPSS durchzuführen, gehst du zu "Analysieren" -> "Regression" -> "Binär Logistisch". Dort gibst du deine abhängige Variable (z.B. Pizza-Liebe) und deine unabhängigen Variablen (z.B. Alter, Anzahl der Kochzeitschriften) ein. Klingt doch schon fast wie ein Kinderspiel, oder?

Die Interpretation: Jetzt wird's spannend!

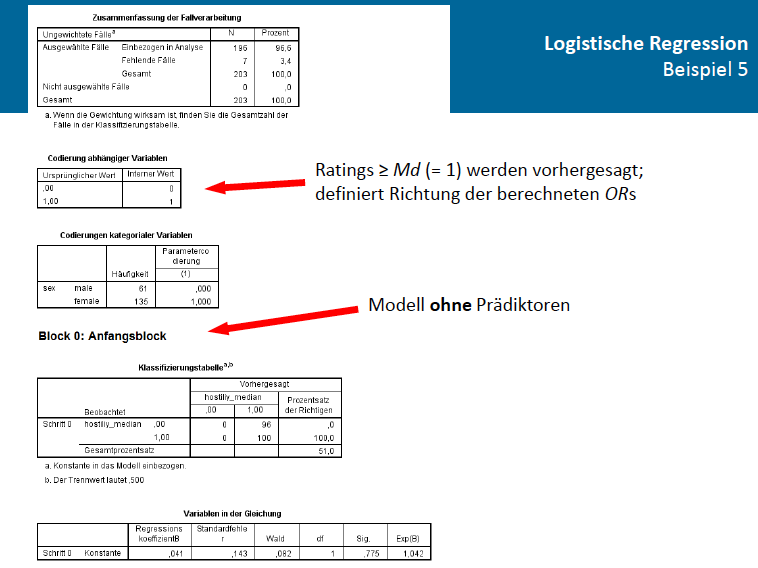
Nachdem SPSS seine Arbeit getan hat, spuckt es eine ganze Menge Zahlen aus. Lass dich davon nicht einschüchtern! Wir konzentrieren uns auf die wichtigen Sachen.

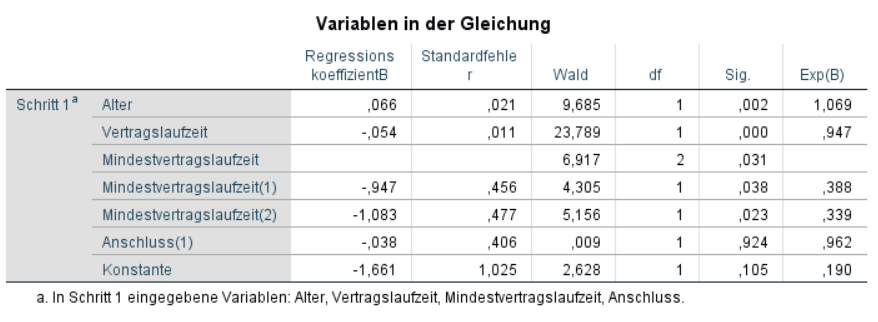
Das B (Beta): Das ist der Koeffizient für jede deiner unabhängigen Variablen. Er sagt dir, wie sich die Log-Odds (die Wahrscheinlichkeit, dass jemand in die "Ja"-Kategorie fällt, geteilt durch die Wahrscheinlichkeit, dass er in die "Nein"-Kategorie fällt) verändern, wenn sich die unabhängige Variable um eine Einheit ändert. Puh, das war jetzt ein Zungenbrecher. Einfacher gesagt: Es zeigt, ob die Variable einen positiven oder negativen Einfluss hat.

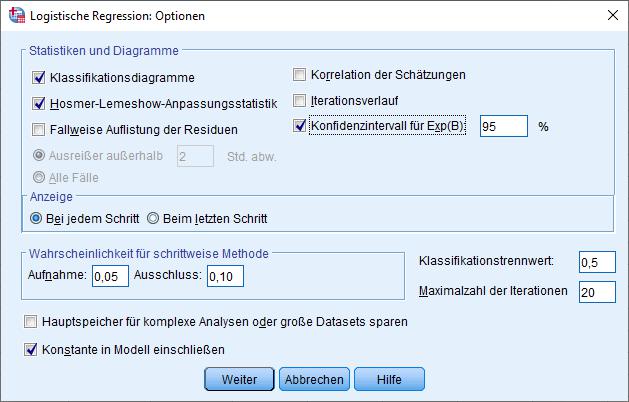
Die Signifikanz (Sig. oder p-Wert): Das ist super wichtig! Sie sagt dir, ob der Einfluss der unabhängigen Variablen *statistisch signifikant* ist. Als Faustregel gilt: Wenn der p-Wert kleiner als 0,05 ist, dann ist der Einfluss signifikant. Das bedeutet, dass es unwahrscheinlich ist, dass das Ergebnis zufällig zustande gekommen ist. Hurra!

Die Odds Ratio (Exp(B)): Das ist der absolute Star der Show! Sie ist einfacher zu interpretieren als das B. Sie sagt dir, um wie viel sich die Odds (nicht die Wahrscheinlichkeit!) verändern, wenn sich die unabhängige Variable um eine Einheit ändert. Eine Odds Ratio über 1 bedeutet einen positiven Einfluss, eine unter 1 einen negativen. Wenn die Odds Ratio für "Alter" z.B. 1.2 beträgt, bedeutet das, dass mit jedem Jahr, das jemand älter wird, die Odds, dass er Pizza mit Ananas mag, um 20% steigen. (Oder so ähnlich. Ich rechne das jetzt nicht im Detail aus...)

Beispiel: Angenommen, wir finden heraus, dass das Alter (signifikant) ist und eine Odds Ratio von 1.1 hat, und die Anzahl der Kochzeitschriften (ebenfalls signifikant) mit einer Odds Ratio von 1.5. Das würde bedeuten: Ältere Leute tendieren eher dazu, Pizza mit Ananas zu lieben, und je mehr Kochzeitschriften jemand abonniert hat, desto höher ist die Wahrscheinlichkeit, dass er auch Pizza mit Ananas mag. Verrückt, oder?

Wichtige Tipps und Tricks (und ein paar Warnungen!)

• Denke an den Kontext! Statistische Signifikanz bedeutet nicht unbedingt praktische Relevanz. Vielleicht ist der Effekt zwar signifikant, aber so klein, dass er keine Rolle spielt.
• Achte auf Multikollinearität! Wenn deine unabhängigen Variablen stark miteinander korrelieren, kann das die Ergebnisse verzerren. SPSS hat Funktionen, um das zu überprüfen.
• Sei vorsichtig mit Kausalität! Nur weil zwei Variablen zusammenhängen, heißt das nicht, dass die eine die andere verursacht. Korrelation ist nicht gleich Kausalität! (Das ist ein Mantra für jeden Statistik-Fan).

Bonus-Tipp: Wenn du dir unsicher bist, schau dir Tutorials online an oder frag einen Statistik-Guru um Hilfe. Es gibt viele Ressourcen da draußen!

Fazit: Du hast es gerockt!

Siehst du? Logistische Regression ist gar nicht so gruselig. Mit ein bisschen Übung kannst du die Welt der binären Vorhersagen erobern. Denk daran: Bleib neugierig, sei kritisch und hab Spaß dabei! Und wenn du das nächste Mal Pizza isst, denk an die Logistische Regression – vielleicht kannst du ja vorhersagen, wer Ananas drauf mag und wer nicht. Viel Erfolg, mein Freund!