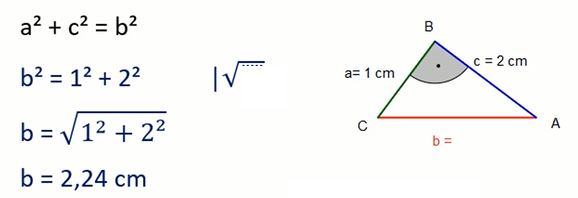Mathe 9 Klasse Realschule Satz Des Pythagoras

Hey! Hast du dich jemals gefragt, wie man die kürzeste Route durch einen Park findet oder wie man überprüft, ob ein Regal wirklich rechtwinklig an der Wand hängt? Dann bist du hier genau richtig! Wir tauchen ein in die faszinierende Welt des Satzes des Pythagoras, einem der beliebtesten und nützlichsten Konzepte, die du in Mathe in der 9. Klasse der Realschule kennenlernst. Keine Sorge, wir machen es locker und verständlich!

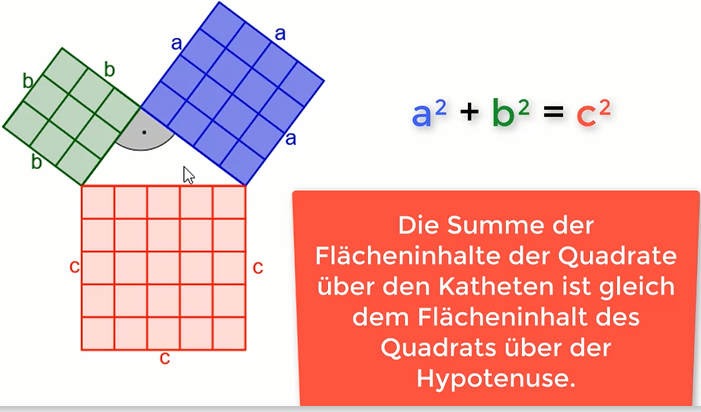
Der Satz des Pythagoras ist wie ein Superhelden-Tool für Rechtwinklige Dreiecke. Er beschreibt nämlich eine ganz spezielle Beziehung zwischen den Seiten dieser Dreiecke. Stell dir vor, du hast ein Dreieck mit einem 90-Grad-Winkel (einem rechten Winkel). Die längste Seite, die dem rechten Winkel gegenüberliegt, nennt man Hypotenuse. Die beiden kürzeren Seiten, die den rechten Winkel bilden, nennt man Katheten. Der Satz des Pythagoras sagt aus: Das Quadrat der Hypotenuse ist gleich der Summe der Quadrate der Katheten. Kurz gesagt: a² + b² = c², wobei a und b die Katheten und c die Hypotenuse sind.

Warum ist das nützlich? Für Anfänger ist es eine super Möglichkeit, das Verständnis für geometrische Formen zu entwickeln und die Verbindung zwischen Algebra und Geometrie zu erkennen. Familien können den Satz nutzen, um beim Heimwerken zu helfen – zum Beispiel, um sicherzustellen, dass ein Bild gerade hängt oder um die Länge einer Diagonale zu berechnen. Und für Hobbyisten, wie zum Beispiel Modellbauer oder Landschaftsgestalter, ist der Satz des Pythagoras ein unschätzbares Werkzeug, um präzise Berechnungen durchzuführen.

Beispiele? Aber klar! Stell dir vor, du willst wissen, wie lang eine Leiter sein muss, um ein Fenster in 4 Metern Höhe zu erreichen, wenn die Leiter 3 Meter vom Haus entfernt steht. Die Wand und der Boden bilden einen rechten Winkel, die Leiter ist die Hypotenuse. Also: 3² + 4² = c² -> 9 + 16 = c² -> 25 = c². Die Wurzel aus 25 ist 5, also muss die Leiter 5 Meter lang sein!

Eine andere Variante: Manchmal ist die Hypotenuse gegeben und eine Kathete gesucht. Zum Beispiel, du hast ein Dreieck mit einer Hypotenuse von 13 cm und einer Kathete von 5 cm. Wie lang ist die andere Kathete? 5² + b² = 13² -> 25 + b² = 169 -> b² = 144 -> b = 12 cm. Auch hier ist die Anwendung ganz einfach.

Einfache Tipps für den Einstieg:

• Visualisiere: Zeichne dir immer eine Skizze des rechtwinkligen Dreiecks, bevor du anfängst zu rechnen. Das hilft enorm beim Verständnis.
• Beschrifte: Markiere die Katheten und die Hypotenuse in deiner Skizze.
• Üben, üben, üben: Je mehr Aufgaben du löst, desto sicherer wirst du im Umgang mit dem Satz des Pythagoras.
• Online-Ressourcen nutzen: Es gibt unzählige Webseiten und Apps, die dir helfen können, den Satz des Pythagoras zu verstehen und zu üben.

Der Satz des Pythagoras ist nicht nur eine Formel, die man auswendig lernt. Er ist ein Schlüssel zum Verständnis der Welt um uns herum und ein fantastisches Werkzeug, um Probleme zu lösen. Also, hab Spaß beim Entdecken und Rechnen!