Multiplizieren Und Dividieren Von Brüchen Klasse 6

Okay, stellt euch vor: Letzte Woche wollte ich einen Kuchen backen. Ein einfaches Rezept, dachte ich. Dann kam der Knaller: "Du brauchst 3/4 Tasse Mehl." Ähm... ja. Bruchrechnen. Plötzlich fühlte ich mich wieder wie in der 6. Klasse, mit Panikattacken vor der Mathearbeit! Wer braucht schon Kuchen, wenn man stattdessen den Weltfrieden retten könnte, oder? Ironie Alarm!
Aber hey, keine Sorge! Wir alle waren mal da. Und Bruchrechnen, besonders das Multiplizieren und Dividieren von Brüchen, ist gar nicht so gruselig, wie es erstmal aussieht. Versprochen! (Ich lüge nie... naja, fast nie.)
Multiplikation von Brüchen: So easy peasy!
Das Multiplizieren von Brüchen ist tatsächlich der einfachste Teil. Ehrlich! Du nimmst einfach den Zähler mal Zähler und den Nenner mal Nenner. Fertig. Bäm!
Also, wenn du 1/2 mal 2/3 rechnen sollst, dann rechnest du 1 * 2 = 2 und 2 * 3 = 6. Das Ergebnis ist also 2/6. (Und ja, das kann man noch kürzen! Dazu später mehr, kleine Streber! 😉)
Merk dir: Kein kompliziertes Gleichnamigmachen nötig! Einfach drauf los multiplizieren. Klingt fast zu schön, um wahr zu sein, oder? Aber es ist wahr! (Fast immer... Ausnahmen bestätigen die Regel, blabla... ihr kennt das Spiel.)
Wenn du eine ganze Zahl mit einem Bruch multiplizieren musst, dann stell dir einfach vor, die ganze Zahl steht auf einem unsichtbaren Nenner von 1. Zum Beispiel: 5 mal 1/4 ist dasselbe wie 5/1 mal 1/4, also 5/4. Et voilà!
Division von Brüchen: Jetzt wird's spiegelverkehrt!
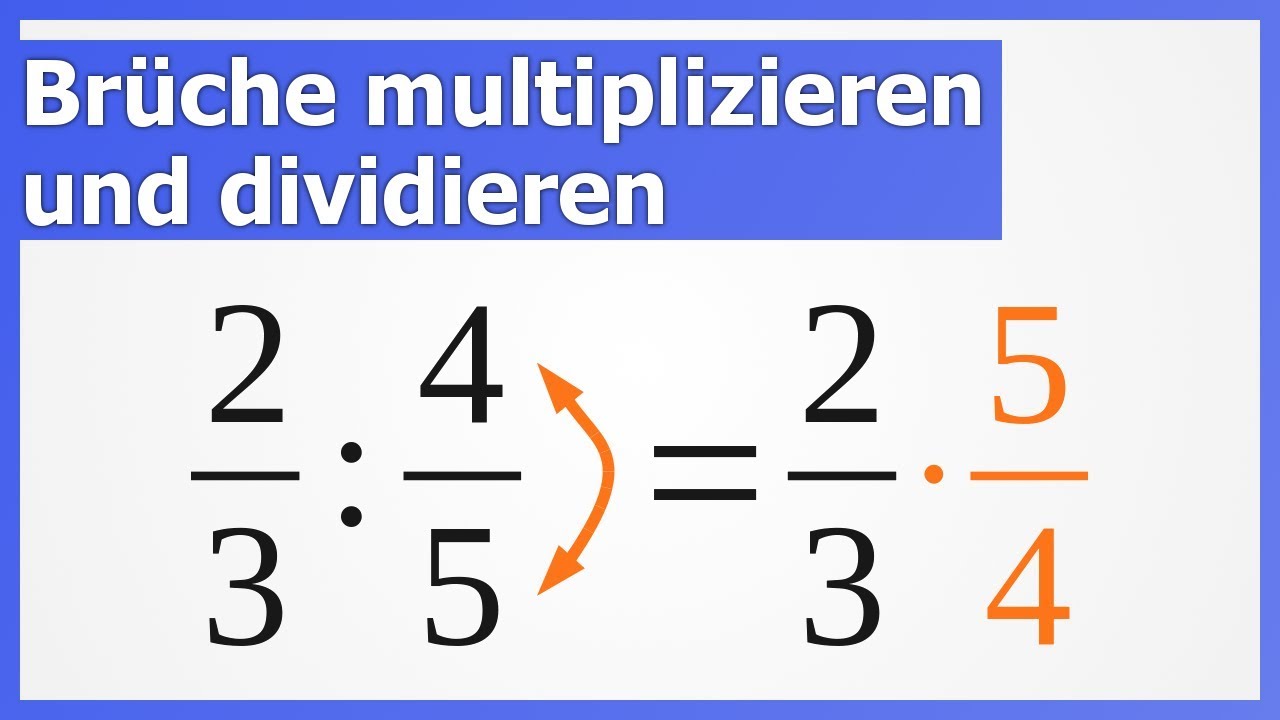
Die Division von Brüchen ist fast genauso einfach, aber mit einem kleinen Trick: Du kehrst den zweiten Bruch um (Zähler und Nenner tauschen die Plätze) und multiplizierst dann! Das nennt man den Kehrwert bilden.
Also, wenn du 1/2 geteilt durch 2/3 rechnen sollst, dann kehrst du 2/3 um, sodass es 3/2 wird. Dann rechnest du 1/2 mal 3/2, was 3/4 ergibt.
Denk dran: Du kehrst immer den zweiten Bruch um, nicht den ersten! Sonst kommt Murks raus! (Glaub mir, ich spreche aus Erfahrung... mit verunglückten Kuchen!)
Warum machen wir das überhaupt? Gute Frage! Die Antwort ist ein bisschen kompliziert und hat was mit dem Dividieren durch einen Bruch zu tun, was eigentlich bedeutet, wie oft der Bruch in die erste Zahl passt. Aber für den Moment reicht es, sich zu merken: Umkehren und multiplizieren! *Mathematiker-Geheimnislüfter-Alarm!*
Kürzen nicht vergessen!
Egal ob du multiplizierst oder dividierst, am Ende solltest du das Ergebnis immer so weit wie möglich kürzen. Das bedeutet, du suchst den größten gemeinsamen Teiler (ggT) von Zähler und Nenner und teilst beide durch diesen Teiler. (Erinnert sich noch jemand an den ggT? *Hust, Staub wisch...*)
Wenn du zum Beispiel 2/6 hast, ist der ggT 2. Also teilst du 2 durch 2 und 6 durch 2, und erhältst 1/3. Fertig! Saubere Arbeit!
Tipp: Manchmal kannst du auch schon vor dem Multiplizieren oder Dividieren kürzen. Das macht die Zahlen kleiner und die Rechnung einfacher. Frag deinen Lehrer nach der "Über-Kreuz-Kürzungs-Technik". (Klingt total geheimnisvoll, ist aber eigentlich ganz logisch.)
Also, jetzt bist du gewappnet für die Welt der Bruchmultiplikation und -division! Und wer weiß, vielleicht backst du ja bald auch einen Kuchen. Oder rettest den Weltfrieden. Oder beides! 😉 Viel Erfolg!