Nullstellen Einer Linearen Funktion Berechnen

Ich erinnere mich noch gut an meinen ersten Versuch, eine Nullstelle zu berechnen. Es war in der 8. Klasse, und ich dachte, Mathematik sei eine Geheimsprache, die nur von Eingeweihten verstanden wird. Ich starrte auf diese kryptische Gleichung – irgendwas mit einem 'x' und einer '5' und einem Minuszeichen – und fühlte mich komplett verloren. (Kennst du das Gefühl? Nicht verzweifeln!) Aber hey, wir alle fangen mal klein an, richtig?

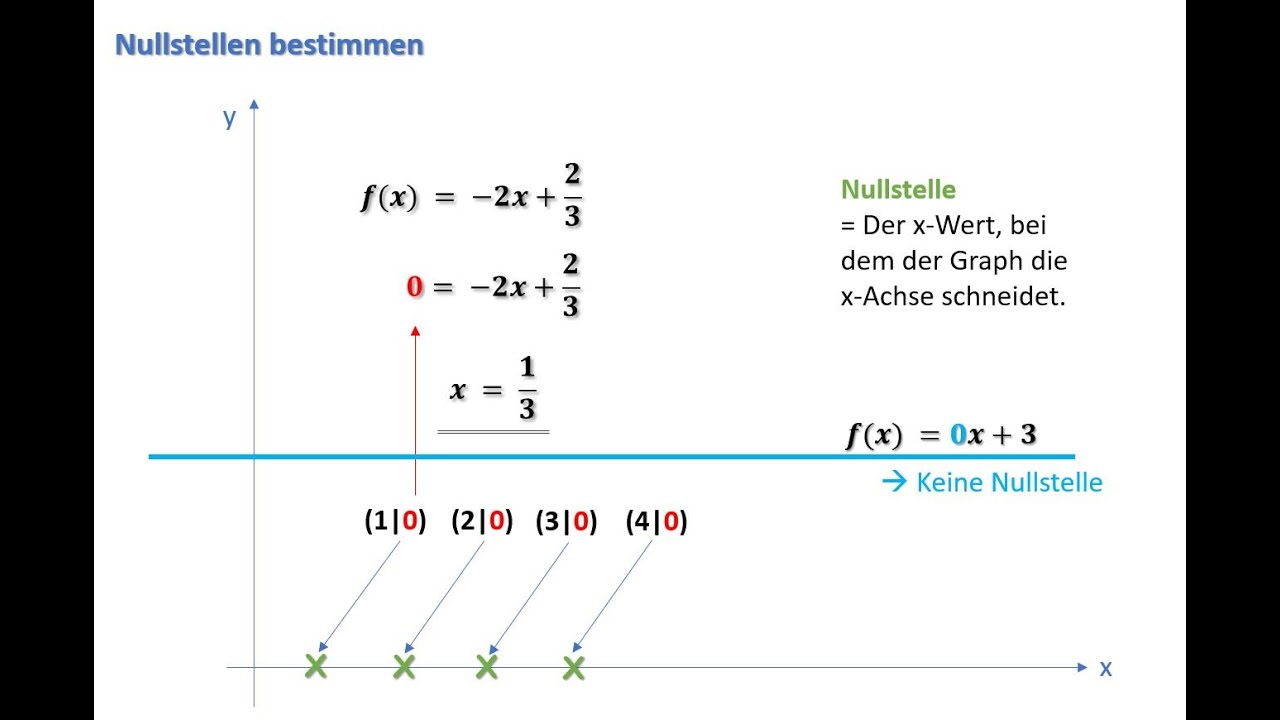
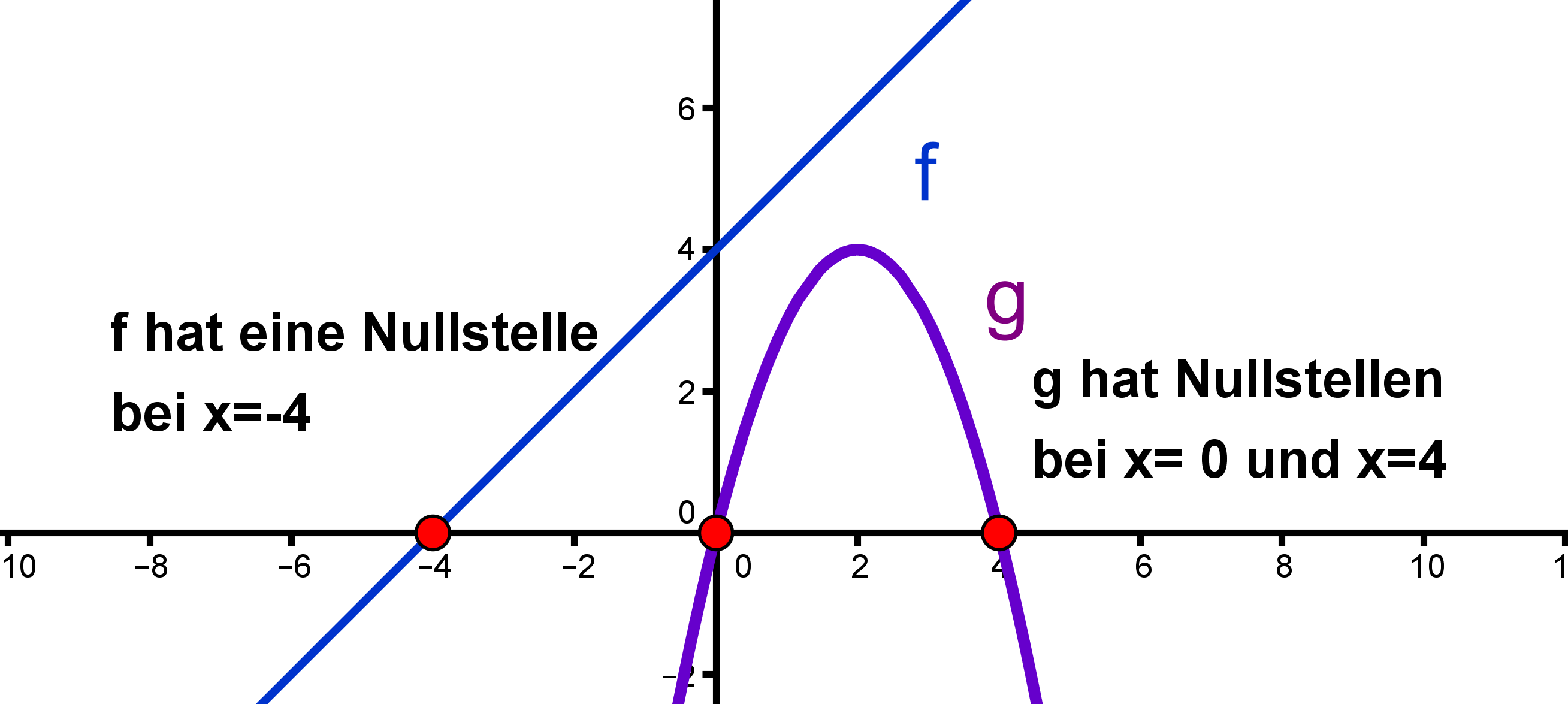
Also, was genau ist diese mysteriöse "Nullstelle", von der alle reden, und warum sollten wir uns überhaupt darum kümmern? Im Grunde ist die Nullstelle einer Funktion der Wert von 'x', bei dem die Funktion gleich Null wird. Klingt kompliziert? Ist es aber nicht. Stell dir vor, du hast eine gerade Linie (eine lineare Funktion), und du willst wissen, wo diese Linie die x-Achse schneidet. Genau da ist die Nullstelle! Denk daran, Nullstelle = Schnittpunkt mit der x-Achse.

Lineare Funktionen: Einfach, aber wichtig

Lineare Funktionen sind die einfachsten Funktionen, die es gibt. Sie haben die Form f(x) = mx + b. Dabei ist 'm' die Steigung der Geraden (wie steil sie nach oben oder unten geht) und 'b' der y-Achsenabschnitt (wo die Gerade die y-Achse schneidet).

Warum sind sie so wichtig? Weil sie überall vorkommen! Von simplen Rechnungen im Alltag bis hin zu komplexen Modellen in der Wissenschaft. Und wenn du lineare Funktionen verstehst, hast du schon mal eine gute Grundlage für alles, was danach kommt.

Wie berechnet man die Nullstelle?

Jetzt kommt der spannende Teil: Wie finden wir diese Nullstelle? Keine Panik, es ist einfacher als du denkst! Wir setzen einfach die Funktion gleich Null und lösen nach 'x' auf. Also:

f(x) = mx + b = 0

Und jetzt der magische Trick:

1. Subtrahiere 'b' von beiden Seiten: mx = -b 2. Dividiere beide Seiten durch 'm': x = -b / m

Tadaa! Das ist die Formel für die Nullstelle einer linearen Funktion. Schreib sie dir am besten auf! (Oder noch besser, versteh sie einfach.)

Ein kleines Aber: Was passiert, wenn 'm' gleich Null ist? Dann haben wir entweder keine Nullstelle (wenn b ungleich Null ist) oder unendlich viele Nullstellen (wenn b auch Null ist). Das ist dann eine horizontale Linie, die entweder gar nicht oder überall die x-Achse schneidet.

Ein Beispiel zur Verdeutlichung

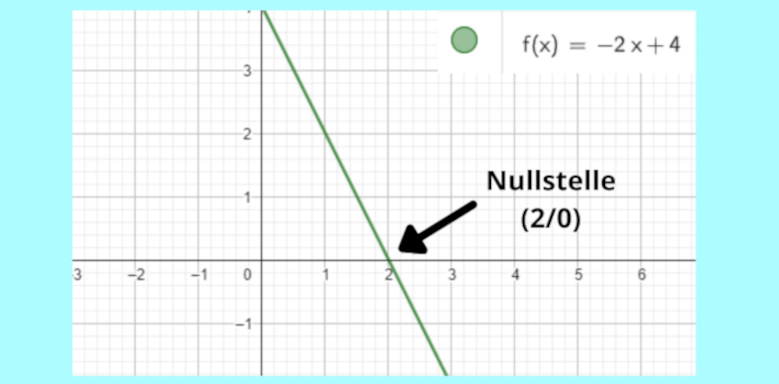
Nehmen wir mal an, wir haben die Funktion f(x) = 2x - 4. Um die Nullstelle zu finden, setzen wir sie gleich Null:

2x - 4 = 0

Addiere 4 auf beiden Seiten:

2x = 4

Dividiere durch 2:

x = 2

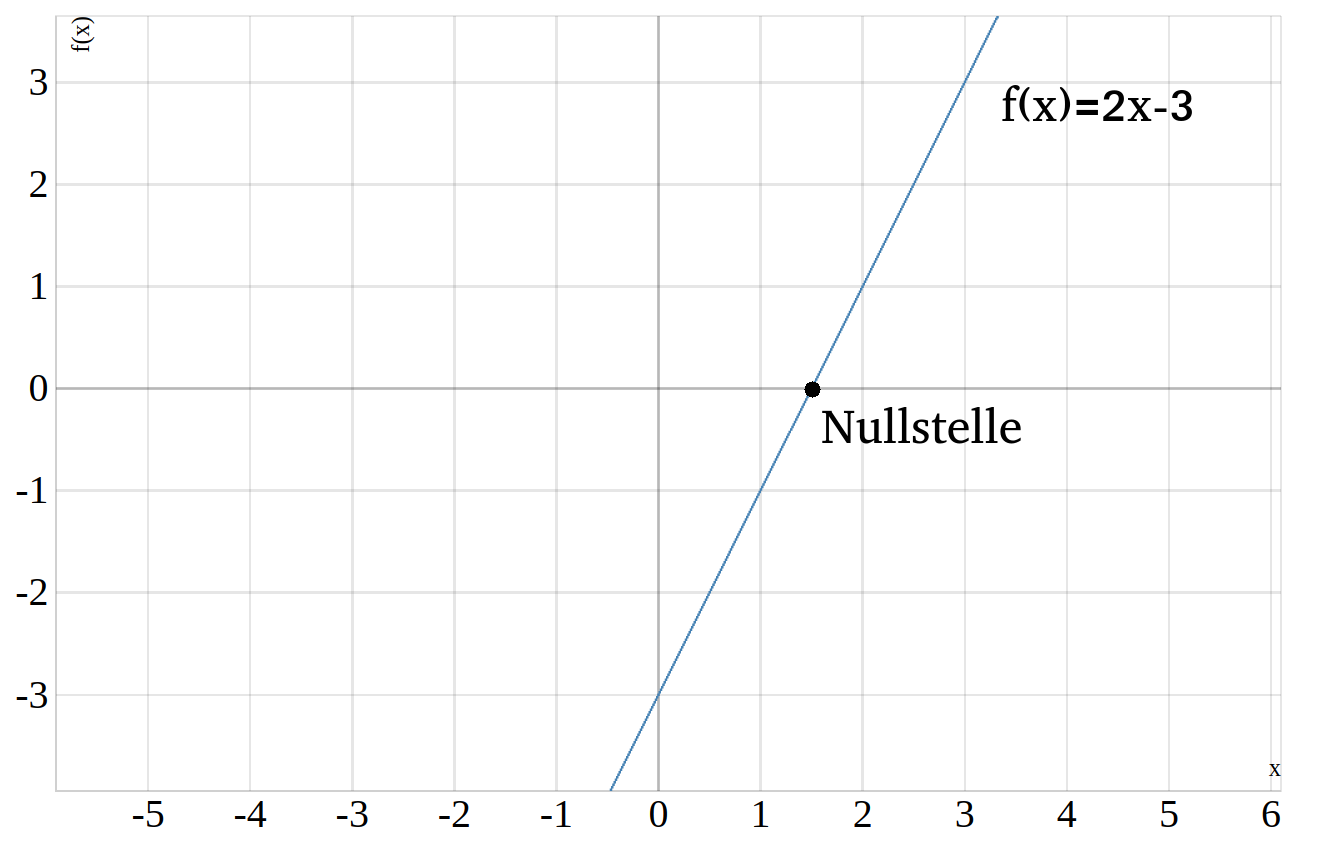
Die Nullstelle ist also x = 2. Das bedeutet, dass die Gerade die x-Achse bei x = 2 schneidet. Easy peasy, oder?

Warum das Ganze?

Okay, jetzt weißt du, wie man Nullstellen berechnet. Aber warum sollte dich das überhaupt interessieren? Nun, Nullstellen sind in vielen Bereichen nützlich. In der Wirtschaft können sie zum Beispiel den Break-Even-Punkt darstellen, also den Punkt, an dem du weder Gewinn noch Verlust machst. In der Physik können sie Gleichgewichtszustände beschreiben. Und in der Mathematik sind sie einfach ein wichtiges Werkzeug, um Funktionen zu verstehen und zu analysieren.

Also, lass dich nicht von der Mathematik einschüchtern! Nullstellen sind nicht so gruselig, wie sie am Anfang vielleicht aussehen. Mit ein bisschen Übung wirst du sie im Schlaf berechnen können. Und wer weiß, vielleicht wirst du ja auch mal ein Mathe-Genie! (Oder zumindest deine Freunde beeindrucken können.) Viel Erfolg!