Potenzen Vereinfachen Mit Unterschiedlicher Basis Und Exponenten

Hey Leute! Habt ihr euch jemals gefragt, wie man eigentlich Potenzen vereinfacht, wenn die Basen so unterschiedlich sind wie Tag und Nacht und die Exponenten auch noch ihr eigenes Ding machen? Keine Sorge, das klingt erstmal komplizierter als es ist. Lass uns das mal entspannt angehen!

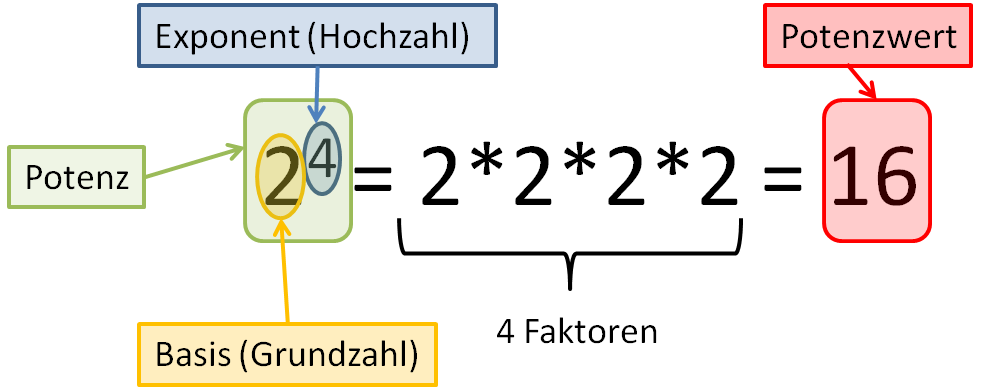
Was sind überhaupt Potenzen? Denk an eine Potenz wie eine Kurzschreibweise für wiederholtes Multiplizieren. Zum Beispiel bedeutet 2³ nichts anderes als 2 * 2 * 2. Easy, oder?

Das Problem mit den unterschiedlichen Basen und Exponenten. Stell dir vor, du hast 2³ und 3². Kann man die irgendwie zusammenfassen? Tja, direkt geht das leider nicht. Das ist, als ob du versuchen würdest, Äpfel mit Birnen zu vergleichen. Aber keine Panik, es gibt trotzdem coole Tricks!

Warum ist das überhaupt interessant?

Okay, mag sein, dass das Vereinfachen von Potenzen mit unterschiedlichen Basen und Exponenten im ersten Moment nicht wie die spannendste Sache der Welt klingt. Aber hey, Mathematik ist wie ein Werkzeugkasten. Je mehr Werkzeuge du kennst, desto besser kannst du Probleme lösen! Und Potenzen tauchen überall auf – in der Informatik, der Physik, der Finanzwelt… Überall!

Denk mal an Computer. Alles, was ein Computer macht, basiert auf Binärcode, also auf Nullen und Einsen. Und diese Nullen und Einsen lassen sich wunderbar mit Potenzen von 2 darstellen. Je besser du also Potenzen verstehst, desto besser verstehst du auch, wie dein Computer funktioniert!

Oder nehmen wir mal die Zinsrechnung. Wenn du Geld anlegst, wächst dein Kapital exponentiell. Und das Verständnis von Potenzen hilft dir, zu verstehen, wie dein Geld sich vermehrt (oder eben auch nicht!).

Der Schlüssel: Gemeinsame Basis oder Exponent

Der Trick beim Vereinfachen von Potenzen mit unterschiedlichen Basen und Exponenten ist, entweder eine gemeinsame Basis oder einen gemeinsamen Exponenten zu finden. Klingt kompliziert? Ist es aber nicht wirklich.

Gemeinsame Basis: Manchmal, mit etwas Trickserei, kannst du die Basen der Potenzen so umformen, dass sie gleich werden. Stell dir vor, du hast 4² und 2³. Wir wissen, dass 4 = 2² ist. Also können wir 4² als (2²)² schreiben. Und jetzt kommt eine wichtige Regel: (a^m)ⁿ = a^m*n. Also wird (2²)² zu 2⁴. Jetzt haben wir 2⁴ und 2³. Bingo!

Jetzt können wir die Potenzen einfach multiplizieren (wenn sie multipliziert werden sollen): 2⁴ * 2³ = 2⁴⁺³ = 2⁷. Easy peasy!

Gemeinsamer Exponent: Das funktioniert ähnlich. Wenn du Potenzen mit dem gleichen Exponenten hast, kannst du die Basen zusammenfassen. Beispiel: 3² * 4². Hier ist der Exponent gleich (2). Wir können das umschreiben als (3 * 4)² = 12². Tadaaa!

Wenn's gar nicht geht…

Manchmal ist es aber auch einfach nicht möglich, eine gemeinsame Basis oder einen gemeinsamen Exponenten zu finden. Was dann? Tja, dann musst du die Potenzen einzeln ausrechnen und das Ergebnis so stehen lassen. Ist auch okay! Nicht jedes Problem lässt sich elegant lösen.

Beispiele zum Ausprobieren

Okay, genug Theorie. Zeit für ein paar Beispiele!

Probiert die Aufgaben einfach mal aus. Keine Angst vor Fehlern! Mathematik ist wie ein Muskel: Je mehr du ihn trainierst, desto stärker wird er.

Fazit: Potenzen sind wie Lego

Potenzen mit unterschiedlichen Basen und Exponenten zu vereinfachen, mag anfangs abschreckend wirken. Aber mit den richtigen Werkzeugen und ein bisschen Übung ist es gar nicht so schwer. Denk an Potenzen wie Lego-Steine. Du kannst sie auf verschiedene Arten zusammensetzen und umformen, um etwas Neues zu erschaffen. Und das ist doch irgendwie cool, oder?

Also, viel Spaß beim Ausprobieren und Knobeln! Und denkt dran: Mathematik muss nicht langweilig sein. Sie kann sogar richtig Spaß machen!