Potenzfunktionen Mit Natürlichen Exponenten
Hey! Na, schon wieder am Mathe-Grübeln? Keine Sorge, ich hab' da was für dich: Potenzfunktionen mit natürlichen Exponenten. Klingt kompliziert, oder? Aber papperlapapp, das kriegen wir easy hin. Stell dir vor, Mathe ist wie ein leckerer Kaffee...nur ohne Koffein-Crash danach. 😉
Was sind Potenzfunktionen überhaupt? Im Grunde genommen ist das eine Funktion, bei der eine Variable (meistens x) mit einer Zahl (dem Exponenten) potenziert wird. Also sowas wie x², x³, x5... du kennst das Spiel! Und das "mit natürlichen Exponenten" bedeutet einfach nur, dass die Zahl oben rechts (der Exponent) eine positive ganze Zahl ist. Keine Brüche, keine negativen Zahlen, nix da. Nur schnöde 1, 2, 3, usw.
Warum sind die Dinger wichtig? Tja, gute Frage! Weil sie überall lauern! In der Physik, in der Informatik, in...na ja, fast überall, wo man irgendwas berechnen muss. Vom Wachstum von Bakterien bis zur Flugbahn einer Rakete – Potenzfunktionen sind am Start. Krass, oder?
Die Basics: Was du wissen musst
Okay, lass uns das mal aufdröseln. Eine Potenzfunktion mit natürlichem Exponenten sieht generell so aus: f(x) = xn. Dabei ist 'x' deine Variable und 'n' dein natürlicher Exponent. Easy peasy, oder?
Was passiert, wenn n = 1 ist? Dann haben wir f(x) = x1, was einfach nur f(x) = x ist. Eine stinknormale Gerade! Fast langweilig, aber jeder fängt mal klein an, gell?
Und wenn n = 2 ist? Zack, f(x) = x². Das ist die berühmte Parabel! Die kennst du doch, oder? So ein U-förmiges Ding. Die ist schon ein bisschen spannender, weil sie uns zeigt, dass Quadrate immer positiv sind (oder Null, wenn x = 0 ist). Clever, nicht?
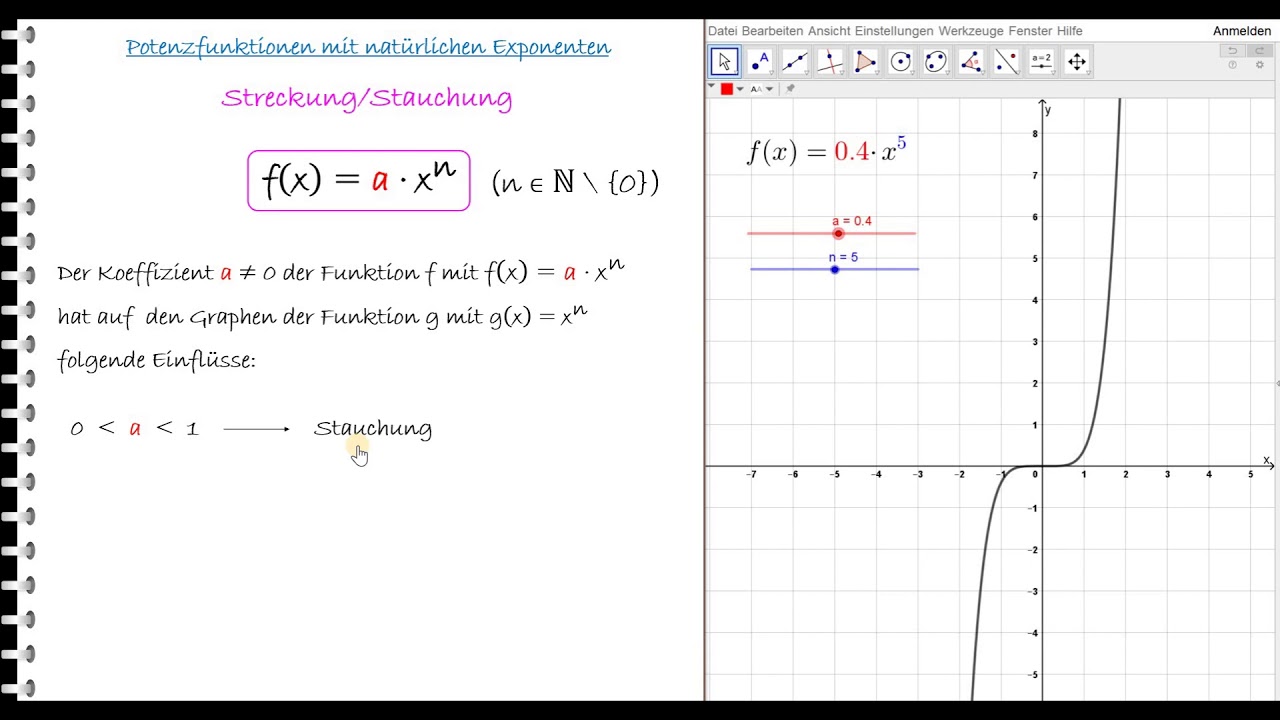
Was passiert, wenn n größer wird? Stell dir vor, du schmeißt noch mehr Zucker in deinen Kaffee. Die Kurve wird steiler! Je größer der Exponent, desto schneller steigt oder fällt die Funktion. Besonders weit weg von der Null. Denk an x10! Das Ding schießt ab wie eine Rakete!
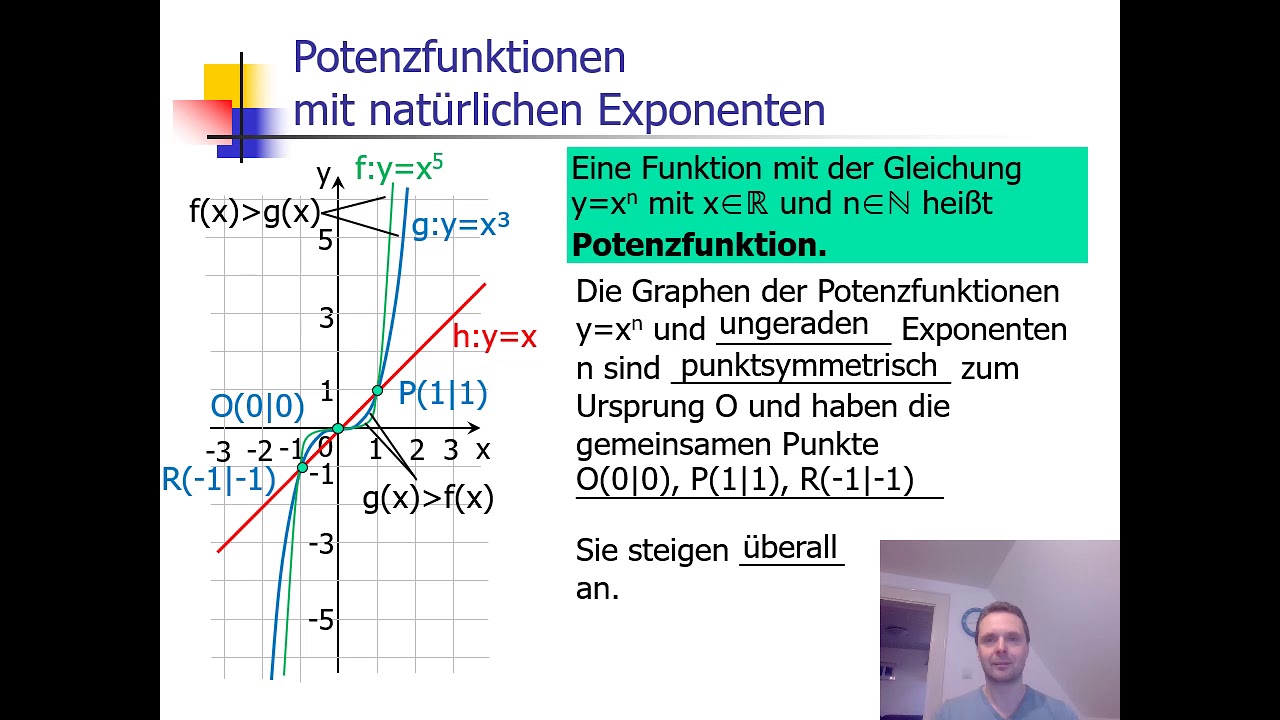
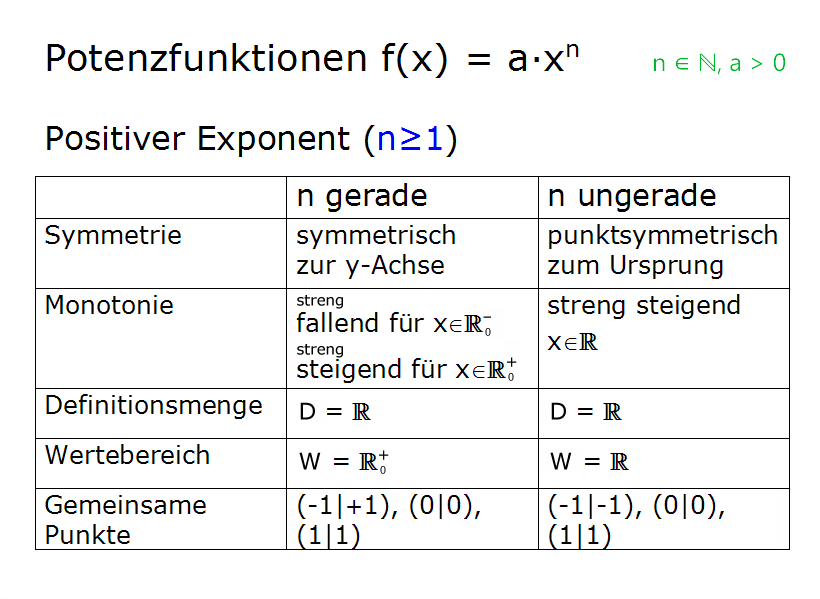
Wichtig: Wenn 'n' gerade ist (2, 4, 6,...), ist die Funktion symmetrisch zur y-Achse. Das bedeutet, die linke und rechte Seite des Graphen sind Spiegelbilder voneinander. Total ordentlich, diese geraden Exponenten! Wenn 'n' ungerade ist (1, 3, 5,...), ist die Funktion punktsymmetrisch zum Ursprung. Heißt: Drehst du den Graphen um 180 Grad, sieht er immer noch gleich aus. Ein bisschen wilder, diese ungeraden Typen.
Der Graph: Ein Bild sagt mehr als tausend Zahlen
Der Graph einer Potenzfunktion verrät dir schon viel. Er zeigt dir, wie sich die Funktion verhält. Steigt sie? Fällt sie? Wo sind die Nullstellen? Wo sind die Extrempunkte? All das kannst du ablesen. Man muss den Graphen nur richtig deuten können. Stell dir vor, der Graph ist wie eine Landkarte für deine Funktion!
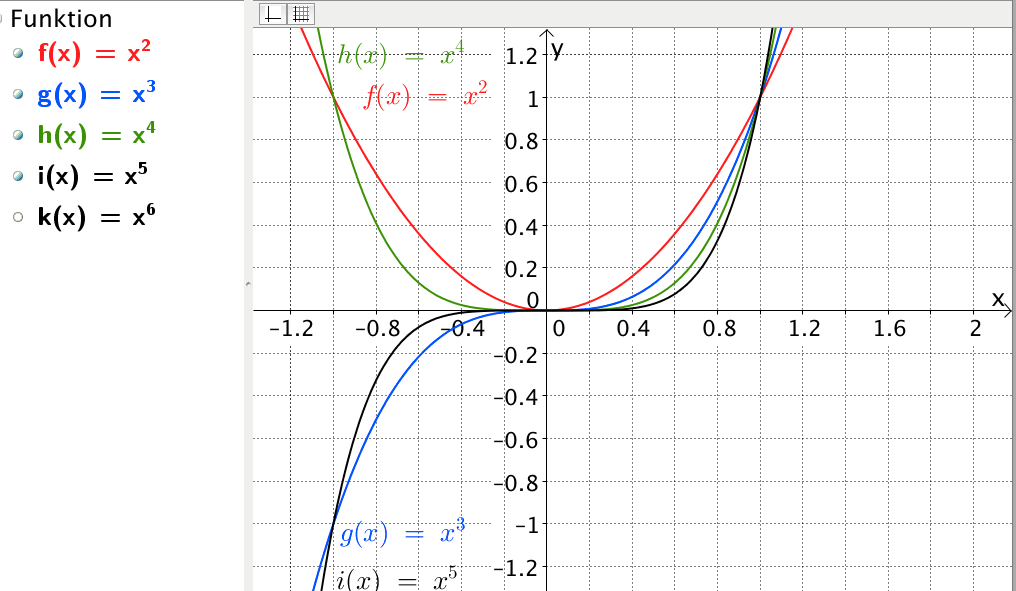
Eine Parabel (x²) hat ihren Scheitelpunkt (tiefsten Punkt) im Ursprung (0,0). Und je größer der Exponent, desto flacher wird die Kurve in der Nähe des Ursprungs und desto steiler wird sie weiter weg davon. Merkst du was? Die Funktion verändert sich ständig!
Anwendungsbeispiele: Wo du sie triffst
Wo begegnen uns diese Potenzfunktionen nun im echten Leben? Hier ein paar Beispiele:
- Flächenberechnung: Die Fläche eines Quadrats ist A = s², wobei 's' die Seitenlänge ist. Bingo! Eine Potenzfunktion!
- Volumenberechnung: Das Volumen eines Würfels ist V = s³, wobei 's' die Seitenlänge ist. Wieder eine Potenzfunktion!
- Physik: Die kinetische Energie eines Objekts ist E = 1/2 * m * v², wobei 'm' die Masse und 'v' die Geschwindigkeit ist. Du ahnst es... eine Potenzfunktion!
Siehst du? Potenzfunktionen sind überall! Man muss nur die Augen offenhalten. Und ein bisschen Mathe verstehen, natürlich. 😉
So, das war's in aller Kürze! Jetzt weißt du Bescheid über Potenzfunktionen mit natürlichen Exponenten. Vielleicht probierst du's mal selbst aus? Schnapp dir einen Stift und Papier und zeichne ein paar Graphen! Oder spiel ein bisschen mit einem Online-Funktionsplotter rum. Es macht Spaß, versprochen! Und wenn du Fragen hast, frag einfach! Mathe ist doch keine Einbahnstraße, oder?