Probability Density And Distribution Function
Hey Leute! Habt ihr euch jemals gefragt, wie man die Wahrscheinlichkeit für etwas nicht-diskretes berechnet? Also, nicht so "Kopf oder Zahl" (da ist die Wahrscheinlichkeit ja ziemlich klar), sondern eher sowas wie "Wie wahrscheinlich ist es, dass ich genau 178,32 cm groß bin?" Hier kommen die Wahrscheinlichkeitsdichte und die Verteilungsfunktion ins Spiel! Klingt kompliziert? Keine Sorge, wir machen das ganz entspannt.
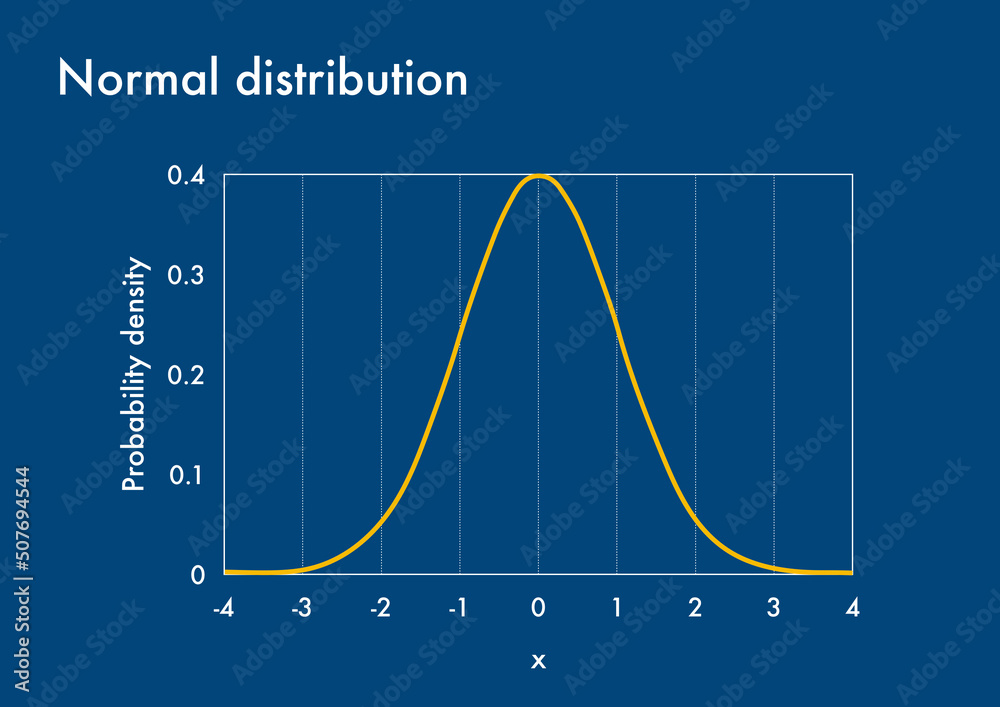
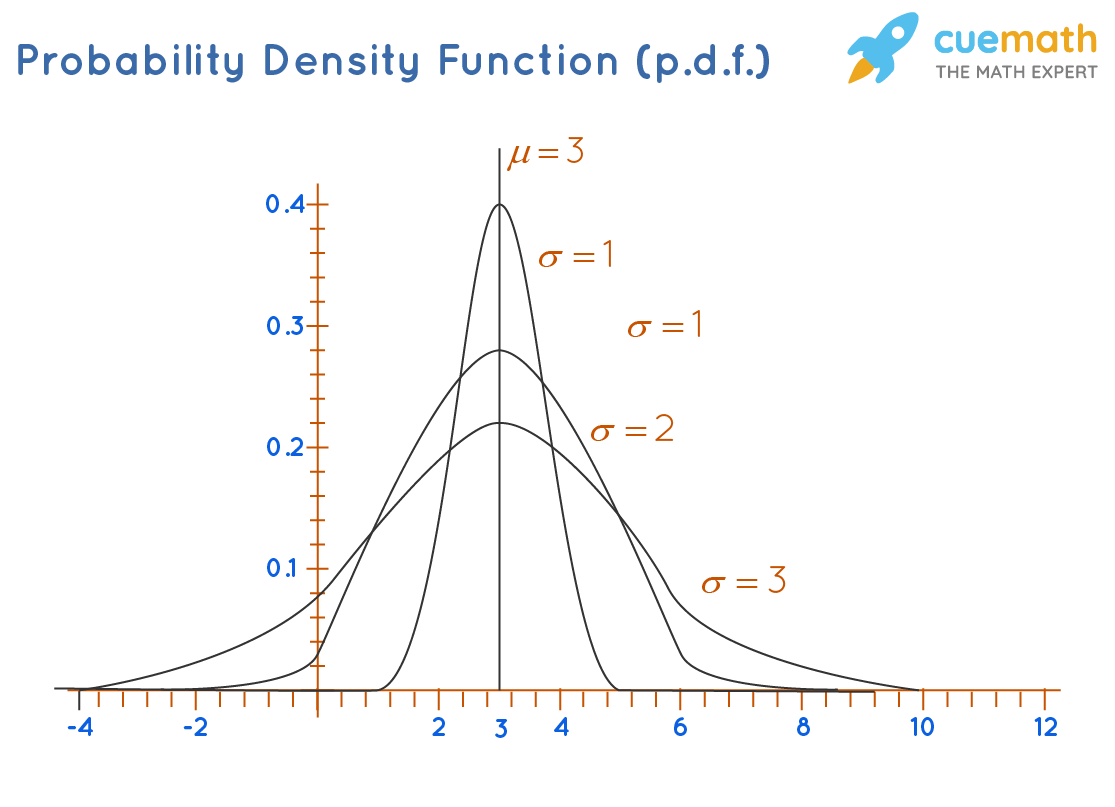
Was ist denn nun diese Wahrscheinlichkeitsdichte?
Stellt euch vor, ihr werft Dartpfeile auf eine Dartscheibe. Nicht auf die Mitte, sondern irgendwie zufällig. Die Wahrscheinlichkeitsdichte (auf Englisch Probability Density Function, kurz PDF) ist wie eine Art Landkarte, die euch zeigt, wo die Dartpfeile am wahrscheinlichsten landen. Wenn ein bestimmter Bereich der Scheibe "dunkelrot" markiert ist, bedeutet das, dass dort viele Pfeile landen. Ein "hellgrüner" Bereich bedeutet hingegen, dass dort eher wenige Pfeile landen.
Aber Achtung: Die Wahrscheinlichkeitsdichte selbst ist noch keine Wahrscheinlichkeit! Sie ist eher ein Maß für die "Dichte" der Wahrscheinlichkeit an einem bestimmten Punkt. Denkt dran, ihr könnt ja nicht "genau" 178,32 cm groß sein. Ihr seid vielleicht 178,321 cm, 178,319 cm, oder irgendwas dazwischen. Die Wahrscheinlichkeitsdichte sagt uns, wie "dicht" die Leute um diese Größe herum verteilt sind.
Ein wichtiger Punkt: Die Fläche unter der gesamten Wahrscheinlichkeitsdichtefunktion ist immer 1. Das bedeutet, dass die Wahrscheinlichkeit, irgendeine Größe zu haben (im Dartscheiben-Beispiel: irgendwo auf der Scheibe zu landen), 100% beträgt. Logisch, oder?
Ist die Wahrscheinlichkeitsdichte hoch, bedeutet das, dass die Wahrscheinlichkeit, einen Wert in dieser Gegend zu finden, größer ist. Ist sie niedrig, ist die Wahrscheinlichkeit geringer. Wie ein stark befahrener Highway im Vergleich zu einer ruhigen Landstraße!
Die Verteilungsfunktion – der Überblick-Meister
Die Verteilungsfunktion (auf Englisch Cumulative Distribution Function, kurz CDF) ist wie ein Navigationssystem für unsere Dartscheibe. Sie sagt uns: "Wie wahrscheinlich ist es, dass ein Dartpfeil innerhalb dieses bestimmten Bereichs landet?". Anstatt nur einen Punkt zu betrachten, betrachtet sie also einen ganzen Bereich.
Sagen wir, wir wollen wissen, wie wahrscheinlich es ist, dass jemand kleiner als 180 cm ist. Die Verteilungsfunktion gibt uns genau diese Wahrscheinlichkeit! Sie summiert quasi die Wahrscheinlichkeitsdichte von ganz links bis zu unserem gewünschten Wert (180 cm in diesem Fall).
Im Dartscheiben-Beispiel: Die Verteilungsfunktion würde uns sagen, wie wahrscheinlich es ist, dass ein Pfeil innerhalb eines bestimmten Kreises landet, anstatt nur an einem bestimmten Punkt. Wie ein Kuchenstück, das immer größer wird, je weiter wir nach rechts gehen!
Die Verteilungsfunktion startet immer bei 0 (ganz links, null Wahrscheinlichkeit) und endet bei 1 (ganz rechts, 100% Wahrscheinlichkeit). Sie ist immer steigend (oder zumindest nicht fallend), da sie immer mehr Wahrscheinlichkeit "aufsammelt", je weiter wir nach rechts gehen. Wie ein Thermometer, das immer höher steigt (oder zumindest gleich bleibt), je wärmer es wird!
Warum ist das cool?
Okay, genug Theorie. Warum ist das Ganze denn nun so spannend? Weil wir mit Wahrscheinlichkeitsdichte und Verteilungsfunktion Vorhersagen treffen können! Wir können beispielsweise vorhersagen, wie viele Menschen in einer bestimmten Altersgruppe bestimmte Krankheiten entwickeln werden, oder wie sich Aktienkurse entwickeln könnten (obwohl das natürlich keine Garantie ist!).
Denkt mal an die Wettervorhersage! Die beruht auch auf Wahrscheinlichkeiten. Wie wahrscheinlich ist es, dass es morgen regnet? Diese Wahrscheinlichkeit wird anhand von Daten und Modellen berechnet, die auf Wahrscheinlichkeitsdichte und Verteilungsfunktionen basieren.
Oder stellt euch vor, ihr entwerft eine neue Software. Ihr könnt die Wahrscheinlichkeitsdichte und Verteilungsfunktion nutzen, um zu analysieren, wie wahrscheinlich es ist, dass Benutzer bestimmte Funktionen nutzen oder Fehler machen. Das hilft euch, die Software benutzerfreundlicher zu gestalten!
Kurz gesagt: Wahrscheinlichkeitsdichte und Verteilungsfunktion sind mächtige Werkzeuge, um die Welt um uns herum besser zu verstehen und Vorhersagen zu treffen. Und das ist doch ziemlich cool, oder?
Also, das nächste Mal, wenn ihr über Wahrscheinlichkeiten stolpert, denkt an die Dartscheibe und das Navigationssystem! Und vergesst nicht: Statistik muss nicht trocken sein!