Proportionale Und Antiproportionale Zuordnungen Aufgaben Mit Lösungen

Hey Leute, habt ihr euch jemals gefragt, warum manche Dinge so gut zusammenpassen? Oder wie ihr beim Backen die Zutatenmenge anpassen könnt, wenn ihr plötzlich doppelt so viele Gäste erwartet? Dann seid ihr hier genau richtig! Wir tauchen ein in die Welt der proportionalen und antiproportionalen Zuordnungen – klingt kompliziert, ist aber super nützlich und, ja, sogar spaßig! Glaubt ihr nicht? Lest weiter!

Stellt euch vor, ihr seid ein Detektiv und müsst Beziehungen zwischen verschiedenen Dingen aufdecken. Das ist genau das, was wir mit proportionalen und antiproportionalen Zuordnungen machen. Der Clou dabei? Wir können Vorhersagen treffen und Probleme lösen. Klingt gut, oder?

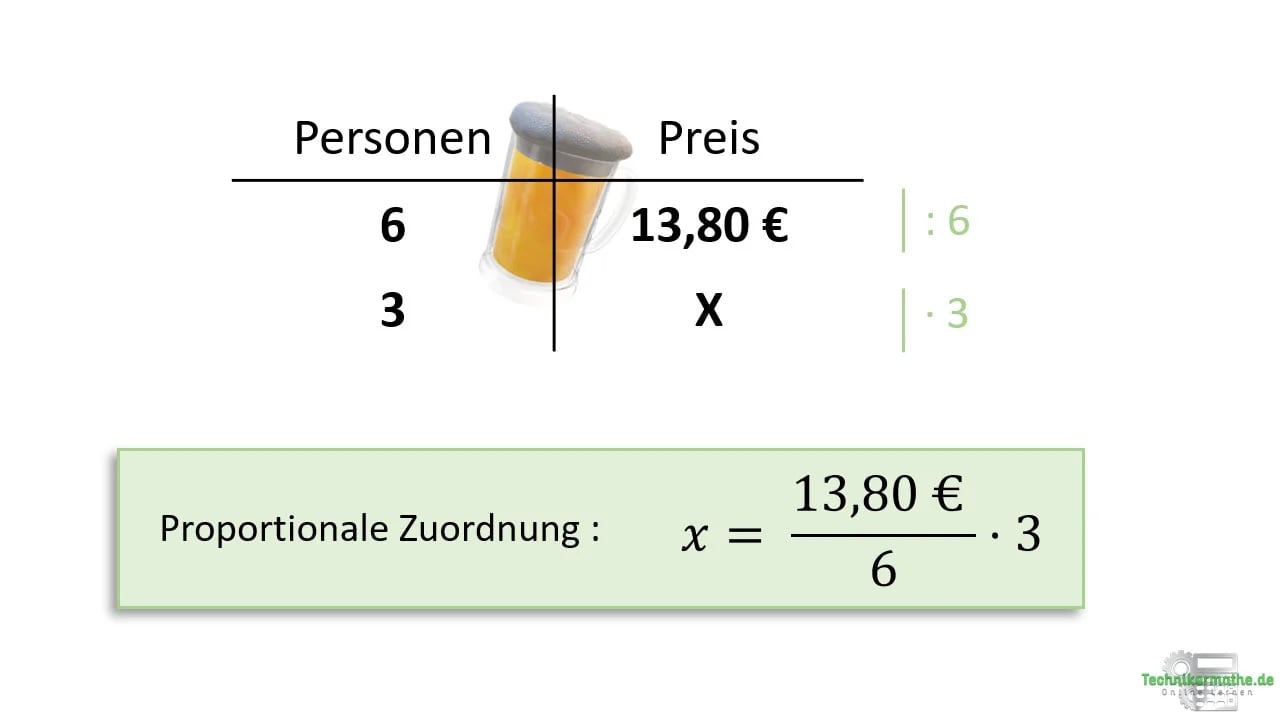
Was ist das Ziel der ganzen Sache? Ganz einfach: Wir wollen verstehen, wie sich zwei Größen zueinander verhalten. Bei einer proportionalen Zuordnung gilt: Wenn das eine steigt, steigt das andere auch – und zwar im gleichen Verhältnis! Denkt an den Preis für Äpfel auf dem Markt. Je mehr Äpfel ihr kauft, desto mehr müsst ihr bezahlen. Die Menge der Äpfel und der Preis sind also direkt proportional zueinander.

Beispiel: Ein Kilo Äpfel kostet 2 Euro. Zwei Kilo kosten 4 Euro, drei Kilo kosten 6 Euro und so weiter. Das Verhältnis bleibt immer gleich: 2 Euro pro Kilo. Das ist super praktisch, denn wenn ihr den Preis für ein Kilo kennt, könnt ihr den Preis für jede beliebige Menge berechnen!

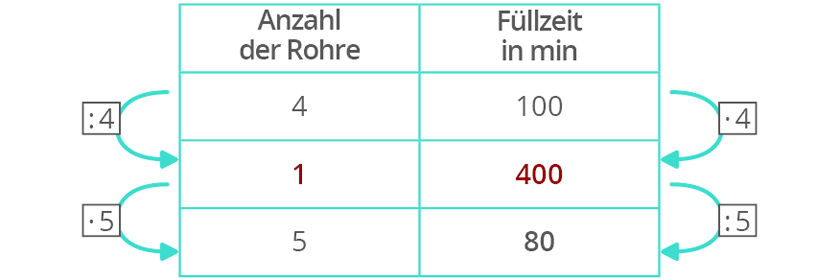
Bei einer antiproportionalen Zuordnung ist es genau umgekehrt. Wenn das eine steigt, sinkt das andere – und zwar so, dass das Produkt der beiden Größen immer gleich bleibt. Denkt an Handwerker, die ein Haus bauen. Je mehr Handwerker mithelfen, desto weniger Zeit brauchen sie, um das Haus fertigzustellen. Die Anzahl der Handwerker und die Bauzeit sind also indirekt proportional zueinander.

Beispiel: Fünf Handwerker brauchen 20 Tage, um ein Haus zu bauen. Wenn zehn Handwerker mithelfen, brauchen sie nur noch 10 Tage. Die Gesamtarbeitszeit (Handwerker x Tage) bleibt immer gleich: 100 Arbeitstage. Je mehr Handwerker, desto weniger Tage – logisch, oder?

Warum ist das Ganze nützlich? Proportionale und antiproportionale Zuordnungen begegnen uns überall im Alltag: Beim Kochen (Zutatenmengen anpassen), beim Einkaufen (Preisvergleiche), beim Planen von Reisen (Geschwindigkeit und Fahrtzeit) und sogar beim Sport (Training und Leistung). Wenn ihr diese Konzepte versteht, könnt ihr bessere Entscheidungen treffen und Probleme schneller lösen.

Aufgaben mit Lösungen? Klar, die gibt es zuhauf! Sucht einfach mal online nach "Proportionale Zuordnung Aufgaben" oder "Antiproportionale Zuordnung Aufgaben". Übung macht den Meister! Lasst euch nicht entmutigen, wenn es am Anfang etwas knifflig ist. Mit etwas Übung werdet ihr bald zum Profi für proportionale und antiproportionale Zuordnungen!

Also, ran an die Aufgaben und viel Spaß beim Entdecken der Welt der Verhältnisse! Ihr werdet sehen, Mathe kann auch spannend sein!