Proportionale Und Antiproportionale Zuordnungen Aufgaben

Wisst ihr, ich hatte letztens so einen Moment im Supermarkt. Ich wollte für eine Party einkaufen und dachte: "Je mehr Leute kommen, desto mehr Pizza brauche ich!" Das war so ein richtiger 'Aha!'-Moment, wo mir klar wurde: Das ist ja direkt proportionale Zuordnung in Reinkultur. Und dann dachte ich: "Ok, aber wenn ich weniger Geld ausgeben will, muss ich vielleicht größere Pizzen kaufen, damit der Preis pro Stück geringer ist." Zack! Antiproportionale Zuordnung! Mathematik lauert überall, Leute! Überall!

Also, lasst uns mal über proportionale und antiproportionale Zuordnungen reden. Klingt kompliziert, ist es aber eigentlich gar nicht. Stell dir vor, du hast zwei Größen, die irgendwie zusammenhängen. Der Zusammenhang ist entweder "direkt" (proportional) oder "indirekt" (antiproportional). Easy, oder?

Proportionale Zuordnungen: Mehr ist mehr!

Bei proportionalen Zuordnungen gilt: Wenn die eine Größe wächst, dann wächst auch die andere. Und zwar im gleichen Verhältnis. Das mit der Pizza war ja schon ein gutes Beispiel. Oder denk an den Stundenlohn: Je mehr Stunden du arbeitest, desto mehr Geld verdienst du. Logisch, oder? Das ist wie mit einer Waage: Auf beiden Seiten muss das Verhältnis stimmen.

Wichtig: Der Quotient bleibt gleich! Das heißt, wenn du die eine Größe durch die andere teilst, kommt immer die gleiche Zahl raus. Diese Zahl nennt man Proportionalitätsfaktor. Merkt euch das, das ist euer Schlüssel zum Erfolg! (Kleiner Tipp: Wenn ihr in einer Aufgabe den Proportionalitätsfaktor berechnen sollt, sucht nach Wörtern wie "pro", "je" oder "für jede/n".)

Eine typische Aufgabe könnte so aussehen: "Drei Äpfel kosten 1,50 €. Wie viel kosten 7 Äpfel?" Du stellst fest: Mehr Äpfel = mehr Kosten. Proportional! Also rechnest du den Preis pro Apfel aus (1,50 € / 3 Äpfel = 0,50 €/Apfel) und multiplizierst das mit der Anzahl der Äpfel, die du kaufen möchtest (0,50 €/Apfel * 7 Äpfel = 3,50 €). Fertig!

Antiproportionale Zuordnungen: Mehr ist weniger!

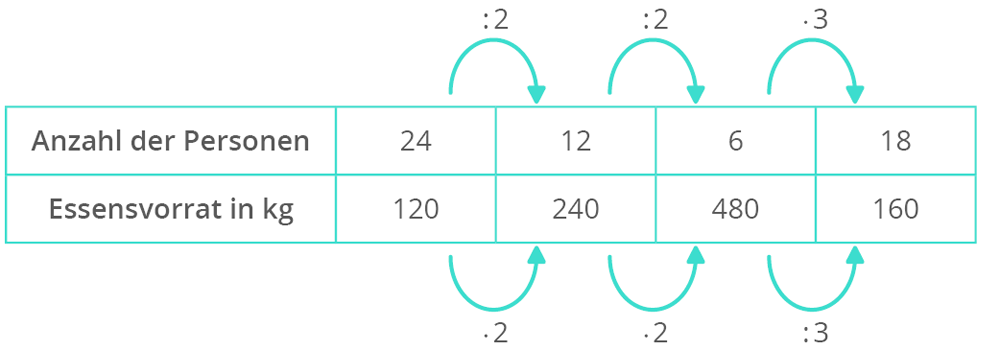
Jetzt kommt der Gegenspieler: Die antiproportionale Zuordnung. Hier ist es genau andersrum. Wenn die eine Größe wächst, dann sinkt die andere. Und zwar so, dass das Produkt der beiden Größen immer gleich bleibt. Denk wieder an die Party: Wenn mehr Leute kommen, muss jeder weniger Pizza essen, damit es für alle reicht. Oder: Je schneller du fährst, desto weniger Zeit brauchst du für eine bestimmte Strecke. Macht Sinn, oder?

Wichtig: Das Produkt bleibt gleich! Das heißt, wenn du die beiden Größen miteinander multiplizierst, kommt immer die gleiche Zahl raus. Diese Zahl nennt man hier... Moment... *denk, denk*... auch Proportionalitätsfaktor! (Ja, ich weiß, verwirrend, aber so ist das nun mal in der Mathematik. Einfach merken!)

So eine Aufgabe könnte lauten: "Drei Arbeiter brauchen 8 Stunden, um eine Mauer zu bauen. Wie lange brauchen 6 Arbeiter?" Du stellst fest: Mehr Arbeiter = weniger Zeit. Antiproportional! Also rechnest du die "Gesamtarbeitszeit" aus (3 Arbeiter * 8 Stunden = 24 Arbeitsstunden). Und dann teilst du das durch die Anzahl der Arbeiter, die du jetzt hast (24 Arbeitsstunden / 6 Arbeiter = 4 Stunden). Voilà!

Kleiner Trick: Wenn ihr euch unsicher seid, ob eine Zuordnung proportional oder antiproportional ist, überlegt euch einfach: "Was passiert mit der anderen Größe, wenn ich die erste verdopple?". Wird sie auch doppelt so groß? Dann ist es proportional. Wird sie halb so groß? Dann ist es antiproportional.

Und noch ein Tipp am Rande: Macht viele Übungsaufgaben! Je mehr ihr übt, desto besser werdet ihr darin, proportionale und antiproportionale Zuordnungen zu erkennen und zu berechnen. Und vergesst nicht: Mathematik kann auch Spaß machen! (Manchmal...)

Also, ran an die Aufgaben und zeigt's dem Mathelehrer! Ihr schafft das!