Rechtwinkliges Dreieck Berechnen Nur Eine Seite Und Ein Winkel Gegeben
Hey du! Hast du jemals vor einem rechtwinkligen Dreieck gestanden und gedacht: "Mist, wie kriege ich denn jetzt die fehlenden Seiten raus?" Keine Sorge, das geht vielen so! Aber keine Panik, es ist einfacher als du denkst. Und glaub mir, wenn du das einmal drauf hast, fühlst du dich wie ein kleiner Mathe-Superheld!
Warum sollte mich das überhaupt interessieren?
Gute Frage! Okay, vielleicht baust du nicht gerade eine Brücke (obwohl, wer weiß!), aber das Wissen um rechtwinklige Dreiecke kann überraschend nützlich sein. Stell dir vor, du willst wissen, wie hoch ein Baum ist. Oder wie lang eine Rampe sein muss. Zack, rechtwinkliges Dreieck, Trigonometrie, Problem gelöst! Außerdem ist es einfach ein cooles Gefühl, wenn du ein Problem mit ein bisschen Mathe lösen kannst, oder? Denk mal an das nächste Mal, wenn du im Baumarkt stehst und die Länge einer Diagonale für ein Projekt ausrechnen musst. Du wirst der Held des Tages sein!
Das magische Werkzeug: Trigonometrie
Jetzt kommt das Zauberwort: Trigonometrie! Klingt kompliziert, ist es aber nicht wirklich. Stell dir einfach vor, es sind coole Helferlein, die dir verraten, wie die Seiten und Winkel in einem rechtwinkligen Dreieck zusammenhängen. Die wichtigsten sind: Sinus (sin), Cosinus (cos) und Tangens (tan). Die kennst du vielleicht schon. Wenn nicht, auch kein Problem, wir frischen das hier kurz auf!
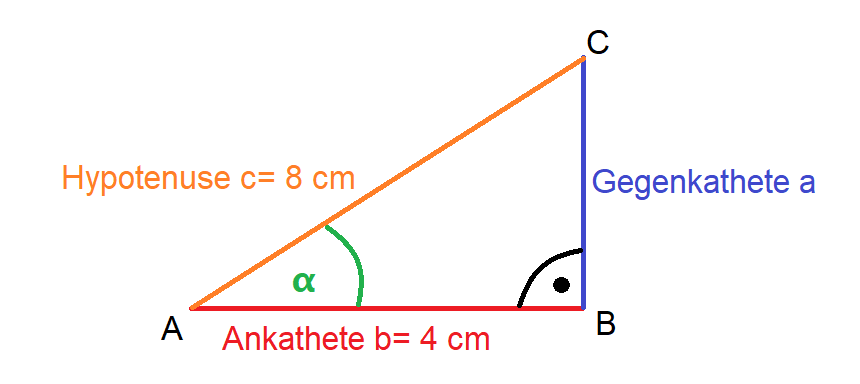
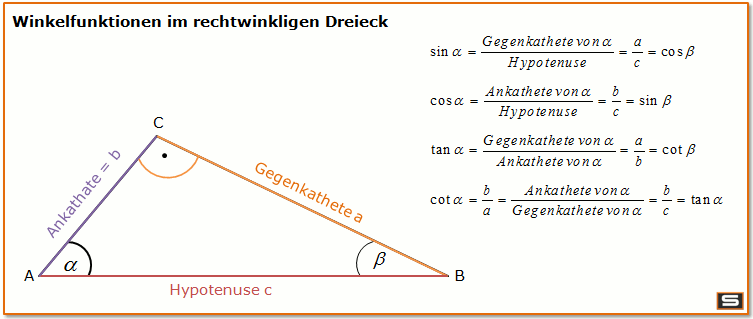
Ein kleines rechtwinkliges Dreieck zur Erinnerung: Wir haben einen rechten Winkel (90 Grad), eine Hypotenuse (die längste Seite, gegenüber dem rechten Winkel), eine Ankathete (die Seite, die am betrachteten Winkel anliegt) und eine Gegenkathete (die Seite, die dem betrachteten Winkel gegenüberliegt). Merke dir das gut!
So, jetzt zu den Helferlein:
- Sinus (sin): Gegenkathete / Hypotenuse
- Cosinus (cos): Ankathete / Hypotenuse
- Tangens (tan): Gegenkathete / Ankathete
Klingt immer noch kompliziert? Keine Sorge, mit einem kleinen Merksatz geht das leichter: Gegenkathete durch Hypotenuse (Sinus), Ankathete durch Hypotenuse (Cosinus), Gegenkathete durch Ankathete (Tangens). "GAGA Hühnerhof AG" ist ein Klassiker! Such dir den Merksatz aus, der dir am besten gefällt!
Rechnen wir mal!
Okay, genug Theorie, jetzt wird's praktisch. Angenommen, du hast ein rechtwinkliges Dreieck, bei dem eine Seite (sagen wir, die Hypotenuse) 5 cm lang ist, und ein Winkel (nicht der rechte Winkel!) beträgt 30 Grad. Du möchtest die Länge der Gegenkathete berechnen. Was machst du?
Ganz einfach: Du überlegst dir, welche trigonometrische Funktion die Gegenkathete und die Hypotenuse ins Spiel bringt. Richtig, der Sinus! Wir wissen:
sin(30°) = Gegenkathete / Hypotenuse
sin(30°) ist 0,5 (das kannst du im Taschenrechner nachschauen oder auswendig lernen). Die Hypotenuse ist 5 cm. Also:
0,5 = Gegenkathete / 5
Jetzt musst du nur noch nach der Gegenkathete auflösen. Das geht, indem du beide Seiten der Gleichung mit 5 multiplizierst:
0,5 * 5 = Gegenkathete
2,5 = Gegenkathete
Tada! Die Gegenkathete ist 2,5 cm lang. Siehst du? Gar nicht so schwer, oder?
Noch ein Beispiel, weil's so Spaß macht!
Sagen wir, du hast die Ankathete mit 4 cm und einen Winkel von 45 Grad. Du möchtest die Gegenkathete berechnen. Welche Funktion hilft dir jetzt? Richtig, der Tangens!
tan(45°) = Gegenkathete / Ankathete
tan(45°) ist 1. Die Ankathete ist 4 cm. Also:
1 = Gegenkathete / 4
Wieder auflösen:
1 * 4 = Gegenkathete
4 = Gegenkathete
Die Gegenkathete ist also 4 cm lang. Perfekt!
Wichtig zu beachten!
Achte immer darauf, dass dein Taschenrechner auf das richtige Winkelmaß eingestellt ist (Grad oder Rad). Das ist ein typischer Fehler, der schnell passiert. Und üben, üben, üben! Je mehr du übst, desto leichter fällt es dir.
Fazit: Du kannst das!
Siehst du? Rechtwinklige Dreiecke sind gar nicht so gruselig. Mit ein bisschen Trigonometrie und etwas Übung kannst du die fehlenden Seiten und Winkel ganz einfach berechnen. Und das Beste daran: Du fühlst dich danach einfach schlauer und selbstbewusster. Also, worauf wartest du noch? Schnapp dir einen Taschenrechner und leg los! Es gibt eine ganze Welt voller geometrischer Herausforderungen, die darauf wartet, von dir gemeistert zu werden! Die Welt der Mathematik ist faszinierend und voller Möglichkeiten. Lass dich darauf ein und entdecke, was du alles erreichen kannst! Das hier war nur der Anfang!