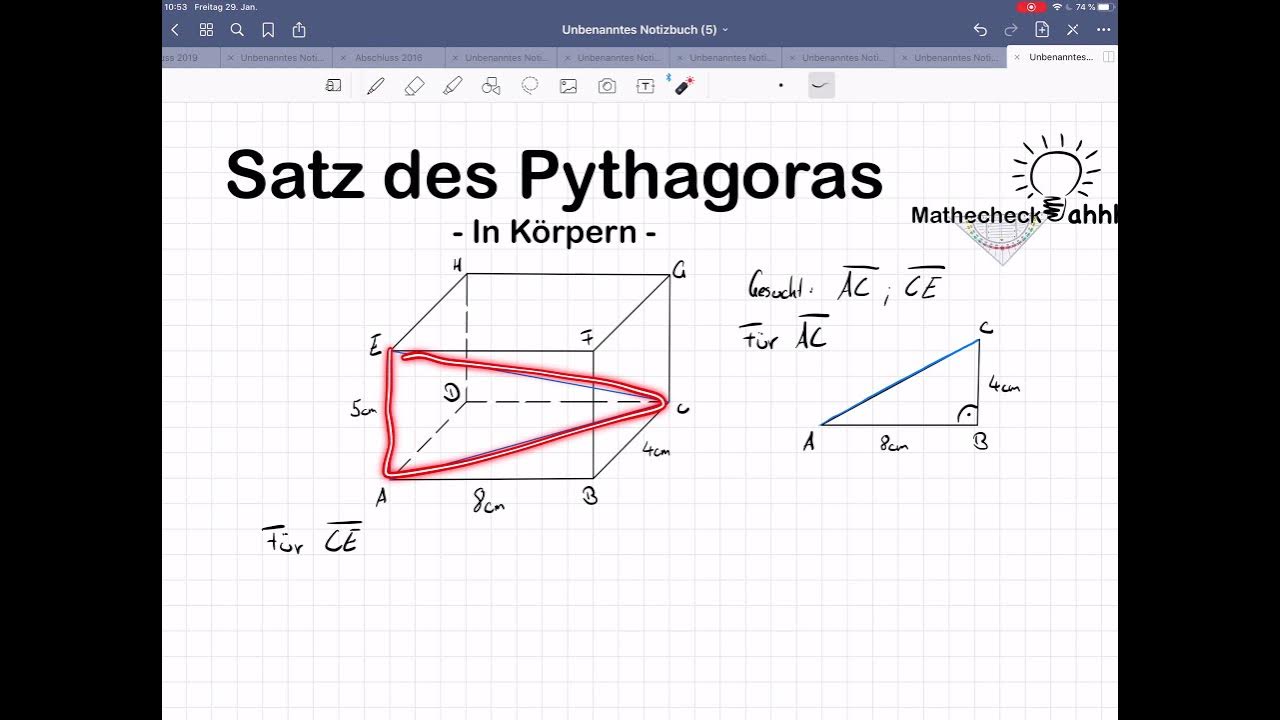
Satz Des Pythagoras In Körpern Aufgaben Pdf

Okay, mal ehrlich: "Satz des Pythagoras in Körpern Aufgaben PDF"... klingt das nicht furchtbar kompliziert? Nach staubtrockenen Mathebüchern und gequältem Stöhnen vor Klassenarbeiten? Aber hey, keine Panik! Wir machen das hier ganz anders. Versprochen!
Vergiss erstmal die PDF. Denk lieber an Pizza. Ja, genau, Pizza! Stell dir vor, du willst die größte Pizza bestellen, die noch in deinen Pizzakarton passt. Der ist quadratisch. Wie findest du raus, welchen Durchmesser die Pizza maximal haben darf? Voilà! Der Satz des Pythagoras kommt ins Spiel!
Oder denk an einen schiefen Baum im Garten. Du willst wissen, wie hoch der Baum ist, aber hinklettern ist zu gefährlich. Mit ein bisschen Messen und dem guten alten Pythagoras kannst du die Höhe trotzdem berechnen. Cool, oder?
Der Satz des Pythagoras, dieser vermeintliche Mathe-Monster, ist im Grunde nur ein super praktisches Werkzeug, um Längen in rechtwinkligen Dreiecken zu berechnen. Und rechtwinklige Dreiecke sind überall!
Was steckt eigentlich hinter dem Pythagoras?
Die Formel lautet: a² + b² = c². Klingt gruselig? Ist es aber nicht! Stell dir vor, du hast ein rechtwinkliges Dreieck. Die beiden kürzeren Seiten, die den rechten Winkel bilden, nennt man Katheten (a und b). Die längste Seite, die dem rechten Winkel gegenüberliegt, ist die Hypotenuse (c).
Der Satz sagt im Prinzip nur aus, dass die Fläche des Quadrats über der Kathete a plus die Fläche des Quadrats über der Kathete b genauso groß ist wie die Fläche des Quadrats über der Hypotenuse c. Denk an kleine Quadrate, die du an die Seiten des Dreiecks malst. Das hilft oft, es sich besser vorzustellen!
Beispiel: Eine Kathete ist 3 cm lang, die andere 4 cm. Dann ist 3² + 4² = 9 + 16 = 25. Also ist c² = 25. Was ist die Wurzel aus 25? Richtig, 5! Die Hypotenuse ist also 5 cm lang.
Pythagoras in 3D: Der Raumdiagonale-Trick
Und jetzt wird's dreidimensional! Hier kommt der "Satz des Pythagoras in Körpern" ins Spiel. Stell dir vor, du hast einen Quader – wie eine Schuhschachtel. Du willst wissen, wie lang die Raumdiagonale ist, also die Linie, die von einer Ecke unten nach diagonal gegenüberliegenden Ecke oben verläuft.
Hier kommt ein kleiner Trick: Zuerst berechnest du die Diagonale der Grundfläche mit dem "normalen" Pythagoras (a² + b² = d²). Diese Diagonale der Grundfläche und die Höhe des Quaders bilden dann wieder ein rechtwinkliges Dreieck. Und schon kannst du mit dem Pythagoras die Raumdiagonale berechnen!
Die Formel für die Raumdiagonale (d) eines Quaders mit den Seitenlängen a, b und c lautet: d² = a² + b² + c².
Beispiel: Stell dir eine Kiste vor, die 40 cm lang, 30 cm breit und 20 cm hoch ist. Die Raumdiagonale wäre dann die Wurzel aus (40² + 30² + 20²) = Wurzel aus (1600 + 900 + 400) = Wurzel aus 2900. Das sind ungefähr 53,85 cm.
Warum du das wissen solltest? (Es ist nützlicher als du denkst!)
Klar, im Alltag wirst du nicht ständig Raumdiagonalen von Schuhkartons ausrechnen. Aber das Prinzip hinter dem Pythagoras hilft dir, räumliches Denken zu entwickeln. Und das ist in vielen Bereichen nützlich:
- Handwerk: Beim Bauen, Zimmern, Fliesenlegen...
- Architektur: Beim Entwerfen von Gebäuden.
- Navigation: Beim Bestimmen von Entfernungen und Richtungen (auch im GPS!).
- Computerspiele: Beim Programmieren von Bewegungen und Kollisionen.
- Einfach so: Um deinen Freunden mit deinem mathematischen Wissen zu beeindrucken! ;-)
Außerdem: Wenn du den Pythagoras verstehst, fühlst du dich einfach schlauer. Und das ist doch auch was wert, oder?
Die Sache mit dem PDF
Jetzt aber zurück zur "Satz des Pythagoras in Körpern Aufgaben PDF". Wenn du das Prinzip verstanden hast, sind die Aufgaben gar nicht mehr so gruselig. Such dir im Internet ein paar Übungsaufgaben und fang einfach an. Wichtig ist, dass du dir die Skizzen genau anschaust und erkennst, wo die rechtwinkligen Dreiecke versteckt sind.
Fang mit einfachen Aufgaben an und steigere dich langsam. Lass dich nicht entmutigen, wenn es am Anfang nicht gleich klappt. Übung macht den Meister, auch beim Pythagoras! Und wenn du mal nicht weiterweißt, gibt es im Internet unzählige Erklärvideos und Foren, wo dir geholfen wird.
Der Satz des Pythagoras ist ein Grundbaustein der Mathematik. Wenn du ihn verstehst, öffnet sich dir eine ganz neue Welt. Also, ran an die PDFs und viel Spaß beim Rechnen! Vielleicht entdeckst du ja sogar deine Freude an der Mathematik. Wer weiß?