Sinus Cosinus Tangens Erklärung Einfach

Erinnerst du dich an den Moment, als du das erste Mal versucht hast, einen IKEA-Schrank zusammenzubauen? Da lagen diese komischen Bretter vor dir, eine Anleitung, die eher wie eine Hieroglyphenschrift aussah, und du hast dich gefragt: "Was zur Hölle mache ich hier eigentlich?" So ähnlich ging es mir mit Sinus, Cosinus und Tangens. Damals in der Schule! Alles war wie ein kryptisches IKEA-Möbelstück für mein Gehirn.

Aber keine Sorge, wir werden hier nicht verzweifeln. Wir werden dieses Trigonometrie-Monster gemeinsam zähmen. Stell dir Sinus, Cosinus und Tangens als **Superkräfte** vor, die dir helfen, Winkel und Seiten in rechtwinkligen Dreiecken zu verstehen. Cool, oder?

Was zum Teufel sind Sinus, Cosinus und Tangens überhaupt?

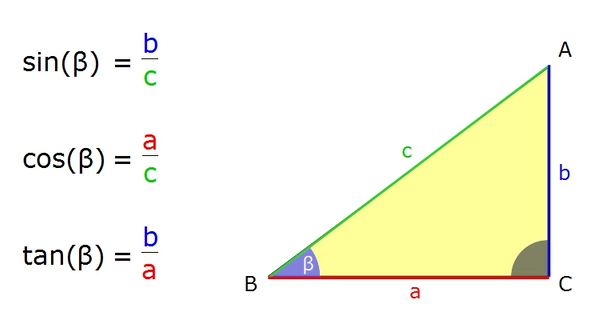
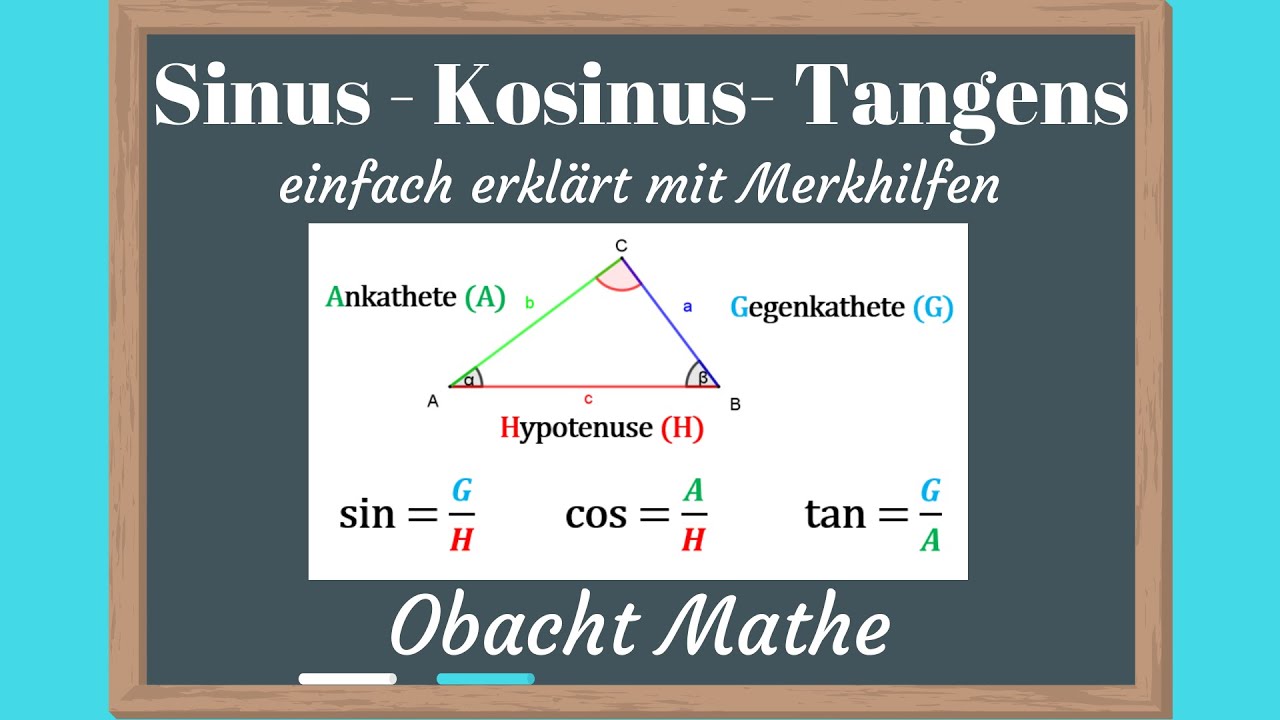
Okay, lass uns das mal ganz basic runterbrechen. Du hast ein rechtwinkliges Dreieck. Das ist wichtig: rechtwinklig! Also mit einem 90-Grad-Winkel. Dann hast du noch einen Winkel (nennen wir ihn mal α - klingt doch schon mal wissenschaftlich, oder?) und drei Seiten:

Hypotenuse: Die längste Seite, die dem rechten Winkel gegenüberliegt. Die Queen des Dreiecks, sozusagen.
Ankathete: Die Seite, die *an* dem Winkel α anliegt. Stell dir vor, sie kuschelt mit dem Winkel.
Gegenkathete: Die Seite, die dem Winkel α *gegenüber* liegt. Sie steht cool und distanziert auf der anderen Seite.

(Merke: Die Hypotenuse ist immer die längste Seite. Easy peasy!)

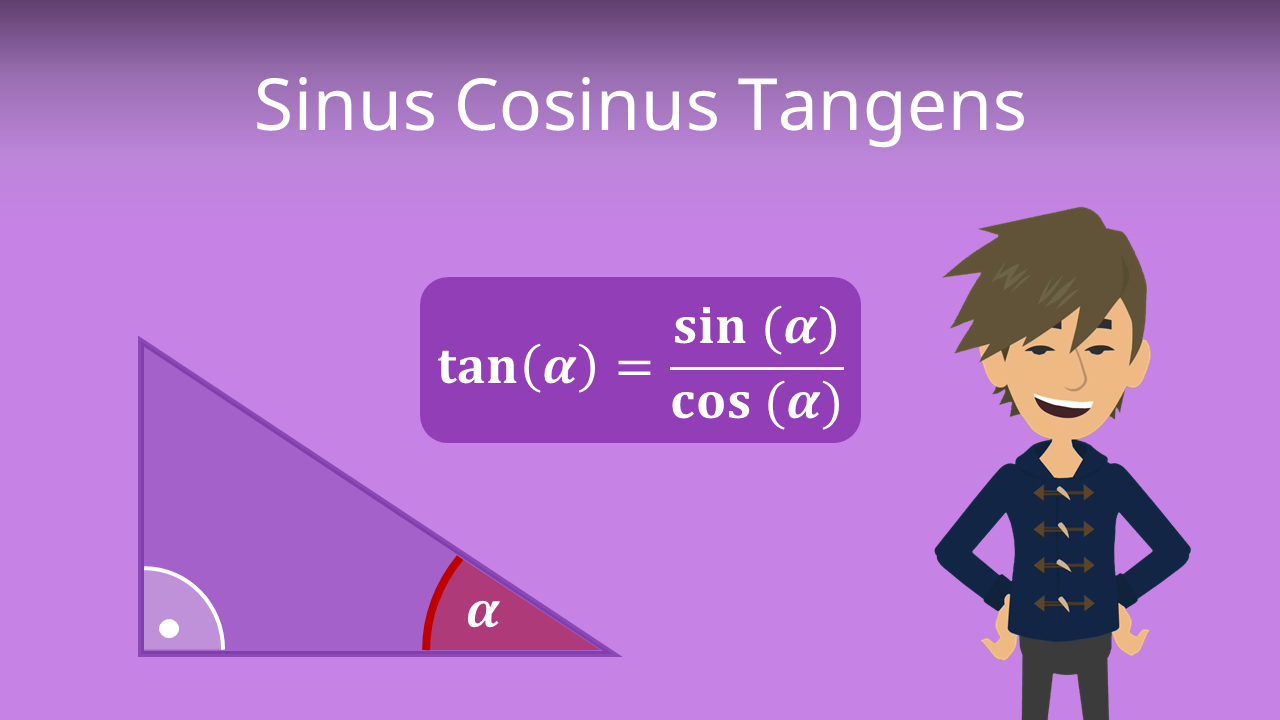
Und jetzt kommt der Clou: Sinus, Cosinus und Tangens sind einfach Verhältnisse dieser Seiten! Klingt kompliziert, ist es aber nicht.

Sinus (sin): Gegenkathete / Hypotenuse. Merke: *G*egen *H*ypotenuse. Eine kleine Gedächtnisstütze.
Cosinus (cos): Ankathete / Hypotenuse. Merke: *A*nkathete *H*ypotenuse. Siehst du das Muster?
Tangens (tan): Gegenkathete / Ankathete. Merke: *G*egenkathete / *A*nkathete. Hier brauchst du keine Hypotenuse!

Also, ganz einfach: Du teilst die Länge einer Seite durch die Länge einer anderen Seite. Und das Ergebnis ist dann der Sinus, Cosinus oder Tangens des Winkels. Boom! Mathematik-Magie!

Warum brauchen wir das überhaupt?

Gute Frage! Warum sollte man sich mit diesem Zeug rumschlagen? Nun, Sinus, Cosinus und Tangens sind super nützlich, wenn du etwas berechnen willst, das mit Winkeln und Entfernungen zu tun hat. Denk an:

Navigation: Flugzeuge, Schiffe, Satelliten – alle nutzen Trigonometrie, um ihren Kurs zu bestimmen. (Du auch, wenn du Google Maps verwendest!)
Architektur und Bauwesen: Um Gebäude stabil und sicher zu konstruieren. (Stell dir vor, ein Wolkenkratzer stürzt ein, weil jemand den Cosinus vergessen hat. Autsch!)
Physik: Um Bewegungen, Kräfte und Wellen zu berechnen. (Klingt kompliziert, aber es ist im Grunde alles nur Sinus und Cosinus!)
Computerspiele: Um realistische Bewegungen und Perspektiven darzustellen. (Deine Lieblingsspiele wären ohne Trigonometrie ziemlich langweilig!)

(Kleiner Tipp: Kauf dir einen Taschenrechner mit Sinus-, Cosinus- und Tangens-Funktion. Das macht das Leben viel einfacher!)

Wie benutzt man Sinus, Cosinus und Tangens?

Okay, genug Theorie. Lass uns ein Beispiel anschauen: Stell dir vor, du stehst vor einem Baum. Du weißt, dass der Winkel zwischen dem Boden und der Baumkrone 30 Grad beträgt. Du gehst 10 Meter vom Baum weg und misst den Winkel. Jetzt willst du wissen, wie hoch der Baum ist.

Hier kommt der Tangens ins Spiel! Du weißt die Länge der Ankathete (10 Meter) und den Winkel (30 Grad). Du willst die Länge der Gegenkathete (die Höhe des Baums) herausfinden.

Also: tan(30°) = Gegenkathete / 10 Meter.

Wenn du das nach der Gegenkathete auflöst, bekommst du: Gegenkathete = tan(30°) * 10 Meter. Dein Taschenrechner (du hast dir doch einen besorgt, oder?) sagt dir, dass tan(30°) ungefähr 0,577 ist. Also: Gegenkathete = 0,577 * 10 Meter = 5,77 Meter. Der Baum ist also ungefähr 5,77 Meter hoch! Voila!

(Achtung: Denk daran, dass dein Taschenrechner auf "Grad" (DEG) eingestellt ist, nicht auf "Radiant" (RAD). Sonst bekommst du komische Ergebnisse!)

Fazit: Keine Panik!

Sinus, Cosinus und Tangens mögen am Anfang einschüchternd wirken, aber mit ein bisschen Übung und den richtigen Eselsbrücken sind sie gar nicht so schlimm. Sie sind wie Werkzeuge in deiner Mathe-Toolbox, die dir helfen, die Welt um dich herum zu verstehen und zu berechnen. Und wer weiß, vielleicht baust du ja eines Tages deinen eigenen Wolkenkratzer – dank Sinus, Cosinus und Tangens!