Standard Deviation And Mean Deviation

Na, schon mal was von Standardabweichung und mittlerer absoluter Abweichung gehört? Klingt erstmal total nach Mathe-Hausaufgaben, oder? Aber glaub mir, dahinter steckt was echt Cooles – und es ist gar nicht so kompliziert, wie es sich anhört! Stell dir vor, du bist auf einer Schatzsuche…genau darum geht es hier irgendwie auch!

Also, was ist das überhaupt? Im Grunde genommen sind das zwei Methoden, um zu verstehen, wie sehr sich eine Gruppe von Zahlen (wir nennen sie mal Daten) um ihren Durchschnittswert streut. Denk an eine Schar von Vögeln: Sind sie alle dicht beieinander oder wild verstreut im Himmel? Genau das wollen wir herausfinden!

Die goldene Mitte: Der Mittelwert

Bevor wir uns in die Abweichungen stürzen, brauchen wir erstmal den Mittelwert, auch Durchschnitt genannt. Der ist super einfach: Du addierst alle Zahlen in deiner Datengruppe und teilst das Ergebnis durch die Anzahl der Zahlen. Stell dir vor, du hast fünf Freunde und ihr habt folgende Anzahl von Süßigkeiten: 2, 4, 6, 8, 10. Der Mittelwert wäre (2+4+6+8+10)/5 = 6. Easy, oder?

Die mittlere absolute Abweichung: Die sanfte Tour

Okay, jetzt wird’s spannend. Die mittlere absolute Abweichung (manchmal kurz MAD genannt) ist wie ein sanfter Spaziergang durch deine Daten. Du nimmst jede Zahl, berechnest ihren Abstand zum Mittelwert (ohne auf Plus oder Minus zu achten, also *absolut*!), addierst all diese Abstände und teilst das Ergebnis wieder durch die Anzahl der Zahlen.

Also, zurück zu unseren Süßigkeiten-Freunden. Der Mittelwert war 6. Die Abweichungen sind: |2-6|=4, |4-6|=2, |6-6|=0, |8-6|=2, |10-6|=4. Die mittlere absolute Abweichung ist dann (4+2+0+2+4)/5 = 2. Das bedeutet, dass die Anzahl der Süßigkeiten im Durchschnitt um 2 vom Mittelwert abweicht.

Warum ist das cool? Weil sie dir einen einfachen und intuitiven Einblick gibt, wie weit deine Daten gestreut sind. Stell dir vor, du vergleichst die MAD von zwei verschiedenen Gruppen von Schülern in einer Klassenarbeit. Die Gruppe mit der kleineren MAD ist homogener – ihre Leistungen sind ähnlicher!

Die Standardabweichung: Der Turbo-Modus

Die Standardabweichung ist sozusagen die fortgeschrittene Version der mittleren absoluten Abweichung. Sie ist etwas komplizierter zu berechnen, aber sie gibt dir ein noch genaueres Bild von der Streuung deiner Daten. Warum? Weil sie die Abweichungen quadriert, bevor sie sie addiert.

Warum quadrieren? Weil das größere Abweichungen stärker gewichtet und kleinere Abweichungen weniger. Das ist nützlich, wenn du Ausreißer in deinen Daten hast – also Werte, die extrem vom Rest abweichen. Stell dir vor, einer deiner Freunde hat plötzlich 100 Süßigkeiten! Die Standardabweichung würde das viel stärker berücksichtigen als die MAD.

Die Berechnung der Standardabweichung sieht so aus: 1. Berechne den Mittelwert (haben wir schon!). 2. Berechne für jede Zahl die Differenz zum Mittelwert und quadriere sie. 3. Addiere alle quadrierten Differenzen. 4. Teile das Ergebnis durch die Anzahl der Zahlen (oder durch die Anzahl der Zahlen minus 1, je nachdem, ob du eine Stichprobe oder die gesamte Population betrachtest – das lassen wir jetzt mal außen vor). 5. Ziehe die Quadratwurzel aus dem Ergebnis. Das ist deine Standardabweichung!

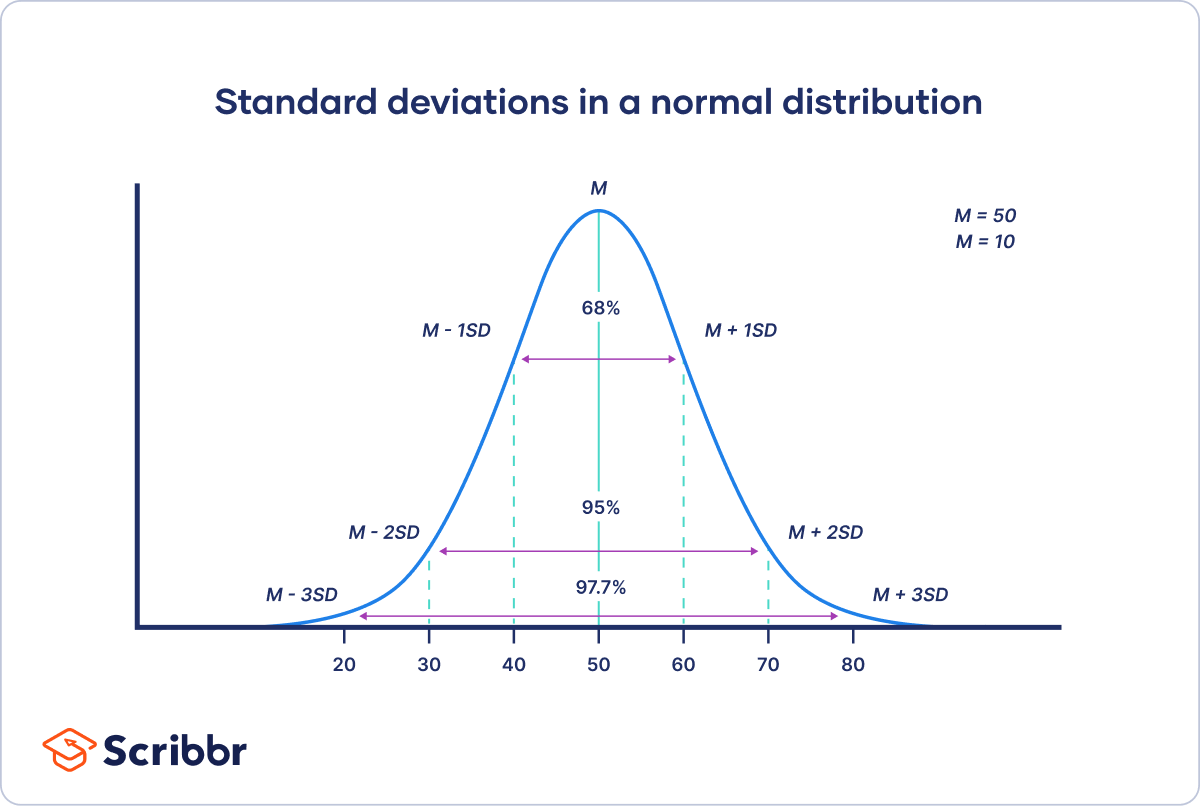
Klingt kompliziert? Keine Sorge, es gibt viele Rechner online, die das für dich erledigen. Wichtig ist, dass du verstehst, was sie aussagt. Eine große Standardabweichung bedeutet, dass deine Daten stark gestreut sind, eine kleine Standardabweichung bedeutet, dass sie dicht beieinander liegen.

Warum ist das alles interessant?

Weil du mit Standardabweichung und mittlerer absoluter Abweichung jede Menge über deine Daten lernen kannst! Ob es um die Leistung von Schülern, die Effizienz einer Fabrik oder die Preise von Immobilien geht – diese beiden Kennzahlen helfen dir, Muster zu erkennen und fundierte Entscheidungen zu treffen.

Denk an Sport: Die Standardabweichung der Wurfweiten eines Basketballspielers zeigt, wie konstant er ist. Je kleiner die Standardabweichung, desto konstanter die Leistung. Oder in der Medizin: Die Standardabweichung des Blutdrucks eines Patienten kann Ärzten helfen, seinen Gesundheitszustand besser einzuschätzen.

Also, das nächste Mal, wenn du über Standardabweichung und mittlere absolute Abweichung stolperst, denk nicht an Mathe-Hausaufgaben, sondern an deine eigene Schatzsuche! Sie sind wie Werkzeuge, die dir helfen, die verborgenen Muster in der Welt um dich herum zu entdecken. Ist doch cool, oder?

Und hey, selbst wenn du nie wieder selbst eine Standardabweichung berechnest, das Verständnis dafür, was sie bedeutet, kann dir im Alltag echt helfen! Wer weiß, vielleicht rettet dir dieses Wissen ja mal den Tag!