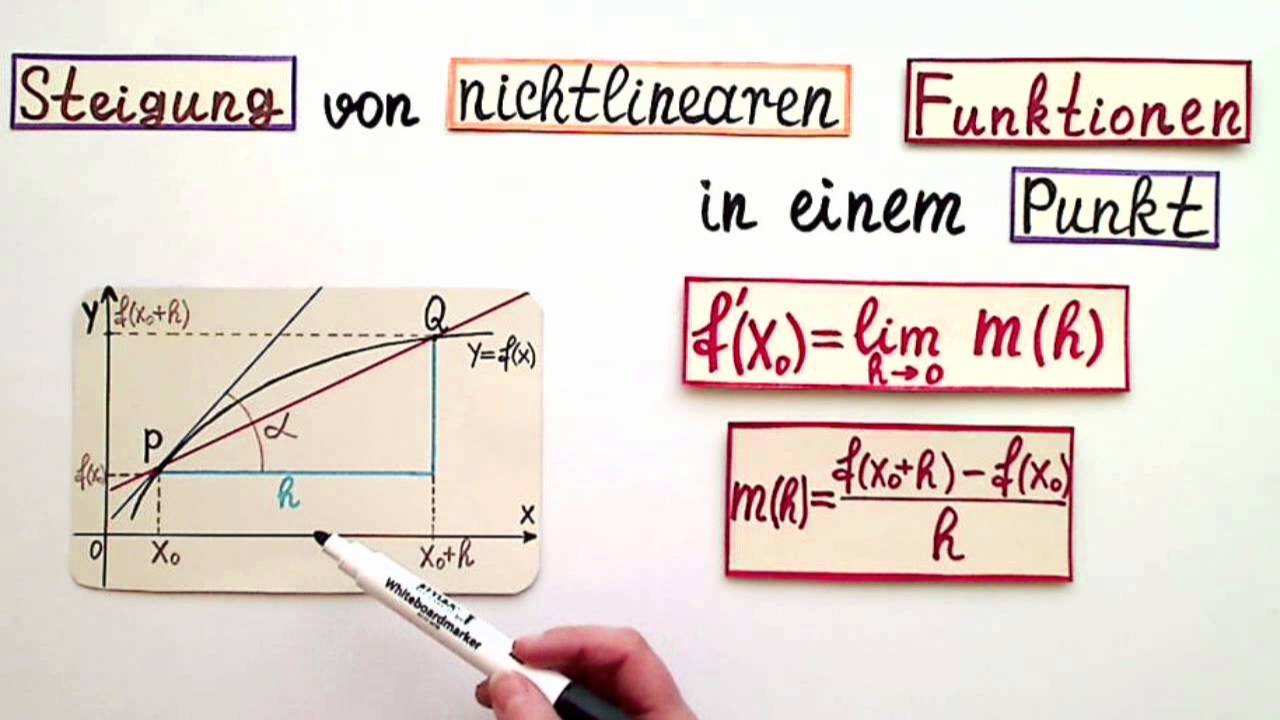
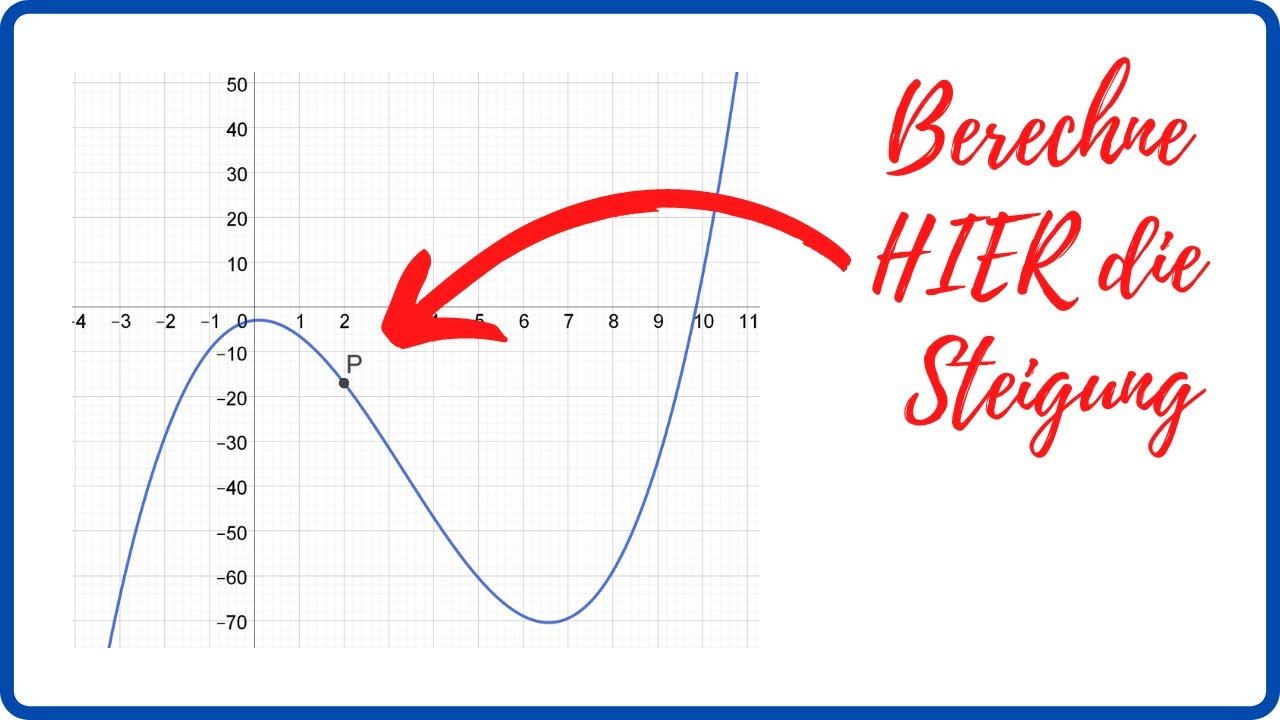
Steigung Des Graphen In Einem Punkt Berechnen
Hey du! Lust auf 'ne kleine Mathe-Party? Keine Sorge, wird nicht öde! Heute geht's um die Steigung. Ja, die Steigung. Am Graphen. An einem einzigen, winzigen Punkt.
Klingt kompliziert? Quatsch! Stell dir vor, du bist auf einer Achterbahn.
Die Steigung sagt dir, wie steil's gerade bergauf oder bergab geht. Ist sie positiv, juchhuu, es geht nach oben! Ist sie negativ, huiii, abwärts!
Was ist überhaupt ein Graph?
Ein Graph ist einfach 'ne Linie. Eine Linie, die irgendeine Funktion darstellt. Denk an y = x² oder sowas. Ist eigentlich ganz easy, oder?
Und die Funktion? Nun, die spuckt dir für jeden x-Wert einen y-Wert aus. Diese Punkte verbindest du, und *tadaaa*, da ist dein Graph!
Die Steigung: Mehr als nur hoch und runter
Die Steigung, die wir suchen, ist aber nicht die Steigung der ganzen Linie. Sondern nur an einem ganz bestimmten Punkt. Mini-Steigung, sozusagen.
Stell dir vor, du sitzt auf der Achterbahn und willst *genau jetzt* wissen, wie steil es ist. Nicht vorher, nicht nachher. Nur jetzt!
Wie findet man die Mini-Steigung?
Hier kommt die Differentiation ins Spiel. Keine Panik, klingt schlimmer als es ist! Stell dir vor, du zoomst immer weiter in deinen Graphen hinein.
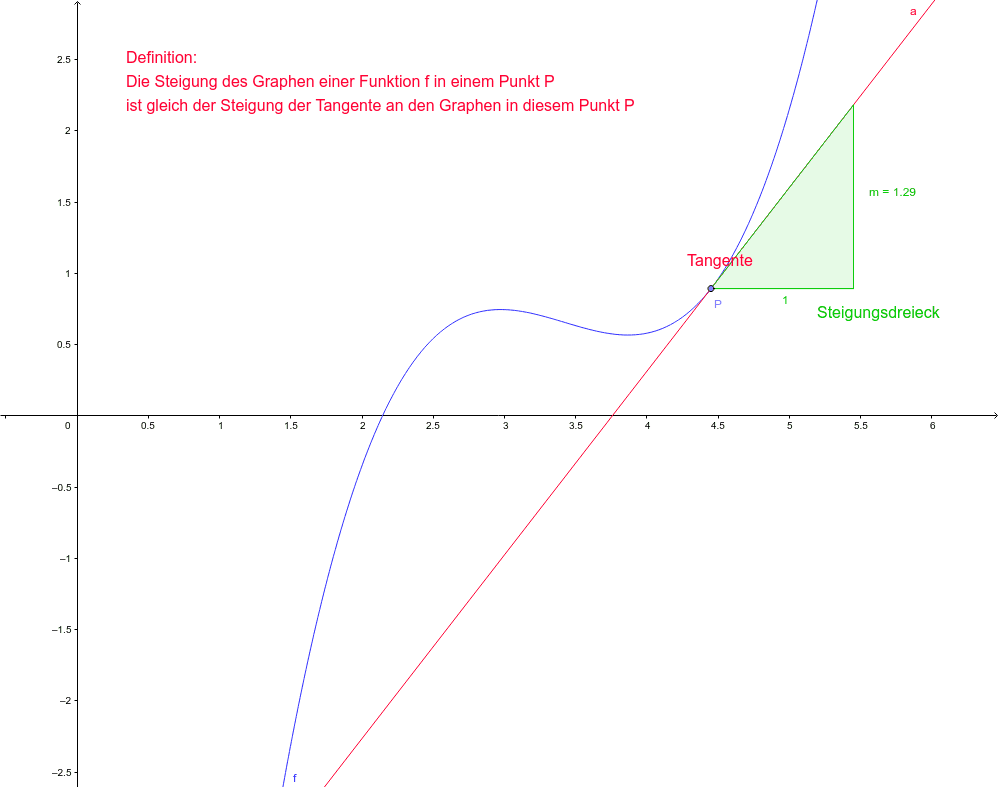
Immer weiter und weiter… Bis der Punkt, an dem du die Steigung suchst, fast wie eine gerade Linie aussieht. Diese gerade Linie ist die Tangente.
Und die Steigung der Tangente? Das ist die Steigung des Graphen an diesem Punkt! Magic!
Die Formel-Sache (aber kurz und schmerzlos!)
Okay, ein bisschen Formel muss sein. Aber keine Angst, wir machen's kurz. Die Ableitung einer Funktion (das ist das, was wir zum Differenzieren brauchen) gibt dir die Steigung an jedem Punkt.
Wenn deine Funktion f(x) = x² ist, dann ist die Ableitung f'(x) = 2x. Einfach den x-Wert einsetzen, und *peng*, Steigung!
Also, bei x = 3 wäre die Steigung 2 * 3 = 6. Zack, erledigt!
Warum ist das eigentlich wichtig?
Gute Frage! Die Steigung ist super nützlich. Denk an:
- Physik: Geschwindigkeit ist die Steigung des Weg-Zeit-Graphen. Beschleunigung ist die Steigung des Geschwindigkeits-Zeit-Graphen. Cool, oder?
- Wirtschaft: Gewinnmaximierung! Die Steigung der Gewinnfunktion sagt dir, wann du am meisten Kohle machst.
- Maschinelles Lernen: Gradientenabstieg! Klingt gefährlich, ist aber nur 'ne Methode, um Computern beizubringen, Sachen zu lernen. Und die Steigung spielt dabei 'ne Riesenrolle!
Ein paar Fun Facts zum Schluss!
Wusstest du, dass…?
- …man die Differentiation auch "Ableitung" nennt? Ist ja logisch, oder? Man leitet die Steigung ab!
- …Leibniz und Newton sich gestritten haben, wer die Differentialrechnung erfunden hat? Echt drama!
- …es Funktionen gibt, die man *nicht* differenzieren kann? Zum Beispiel solche mit Knickstellen. Gemein!
Also, was lernen wir daraus?
Die Steigung eines Graphen an einem Punkt zu berechnen, ist gar nicht so schwer! Mit ein bisschen Übung und dem richtigen Zoom-Faktor (aka Differentiation) kriegst du das locker hin!
Und denk dran: Mathe ist nicht nur Formeln und Zahlen. Es ist ein Werkzeug, um die Welt zu verstehen. Und manchmal macht's sogar richtig Spaß!
Also, geh raus und berechne ein paar Steigungen! Wer weiß, vielleicht entdeckst du ja das nächste große Ding!
Und wenn nicht, hast du wenigstens was gelernt. Und ein bisschen Mathe-Spaß gehabt. Das ist doch auch was, oder?
Viel Spaß beim Steigungen jagen!