Symmetrie Von Ganzrationalen Funktionen

Wir alle lieben Muster, oder? Ob es die perfekt geordneten Fliesen in einem Badezimmer sind, die sich spiegelnden Flügel eines Schmetterlings oder die faszinierende Wiederholung in der Musik – Muster geben uns ein Gefühl von Ordnung, Ästhetik und sogar Vorhersagbarkeit. Aber wussten Sie, dass auch in der Welt der Mathematik, speziell bei ganzrationalen Funktionen, wunderschöne und nützliche Muster existieren, die wir als Symmetrie bezeichnen? Und das Beste daran: Das Verständnis dieser Symmetrien kann uns das Leben erleichtern!

Aber was genau bringt uns die Symmetrie von ganzrationalen Funktionen im Alltag? Stellen Sie sich vor, Sie entwerfen eine Achterbahn. Die Form der Bahn kann durch eine ganzrationale Funktion beschrieben werden. Wenn Sie sicherstellen, dass diese Funktion eine gewisse Symmetrie aufweist (zum Beispiel Achsensymmetrie zur y-Achse), können Sie sicherstellen, dass die Fahrt auf beiden Seiten des höchsten Punktes ähnlich aufregend und sicher ist. Oder denken Sie an die Gestaltung von Brückenbögen, die Modellierung von Schallwellen in der Akustik oder sogar die Analyse von wirtschaftlichen Trends. Überall dort, wo sich Muster wiederholen oder spiegeln, spielen Symmetrieeigenschaften von Funktionen eine entscheidende Rolle.

Ganzrationale Funktionen kennen zwei Hauptarten von Symmetrie: Achsensymmetrie zur y-Achse (auch gerade Funktion genannt) und Punktsymmetrie zum Ursprung (auch ungerade Funktion genannt). Eine Funktion ist achsensymmetrisch, wenn der Graph der Funktion beim Spiegeln an der y-Achse unverändert bleibt. Mathematisch bedeutet das: f(x) = f(-x). Ein klassisches Beispiel hierfür ist die Parabel f(x) = x². Eine Funktion ist punktsymmetrisch zum Ursprung, wenn der Graph der Funktion beim Spiegeln am Ursprung (also einer Drehung um 180 Grad um den Ursprung) unverändert bleibt. Mathematisch bedeutet das: f(x) = -f(-x). Ein typisches Beispiel hierfür ist die Funktion f(x) = x³. Natürlich gibt es auch Funktionen, die weder achsensymmetrisch noch punktsymmetrisch sind. Diese besitzen keine der genannten Symmetriearten.

Wie kann man die Symmetrie einer ganzrationalen Funktion einfacher erkennen? Hier ein paar Tipps:

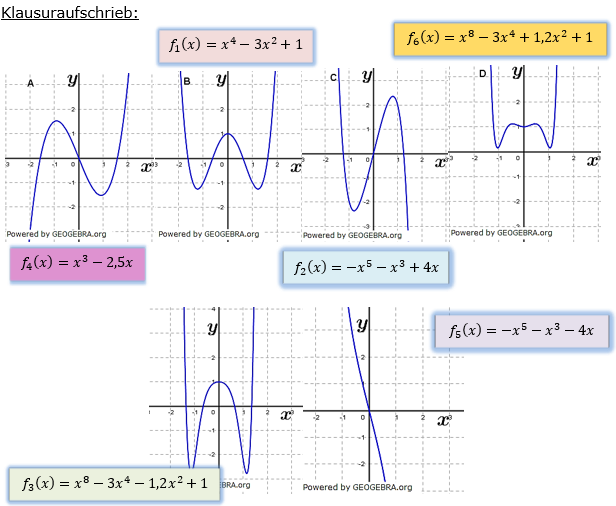
• Betrachten Sie die Exponenten: Sind alle Exponenten gerade, ist die Funktion wahrscheinlich achsensymmetrisch zur y-Achse. Sind alle Exponenten ungerade, ist die Funktion wahrscheinlich punktsymmetrisch zum Ursprung.
• Setzen Sie Werte ein: Wählen Sie ein paar positive und negative Werte für x und berechnen Sie die zugehörigen Funktionswerte. Wenn f(x) = f(-x) gilt, ist die Funktion achsensymmetrisch. Wenn f(x) = -f(-x) gilt, ist sie punktsymmetrisch.
• Nutzen Sie den Graphen: Skizzieren Sie den Graphen der Funktion. Die visuelle Darstellung kann Ihnen sofort Hinweise auf die Symmetrie geben. Viele Taschenrechner und Online-Rechner können das für Sie übernehmen.
• Achten Sie auf Konstanten: Additive Konstanten (z.B. f(x) = x² + 3) beeinflussen die Achsensymmetrie nicht, verschieben aber die Punktsymmetrie. Eine Funktion wie f(x) = x³ + 2 ist nicht punktsymmetrisch!

Das Verständnis der Symmetrie von ganzrationalen Funktionen ist nicht nur eine trockene mathematische Übung. Es ist ein Werkzeug, das uns hilft, die Welt um uns herum besser zu verstehen und Probleme effizienter zu lösen. Also, tauchen Sie ein in die faszinierende Welt der Symmetrie und entdecken Sie die verborgenen Muster, die überall lauern! Es ist eine Fähigkeit, die Ihnen in vielen Bereichen zugutekommen kann – versprochen!