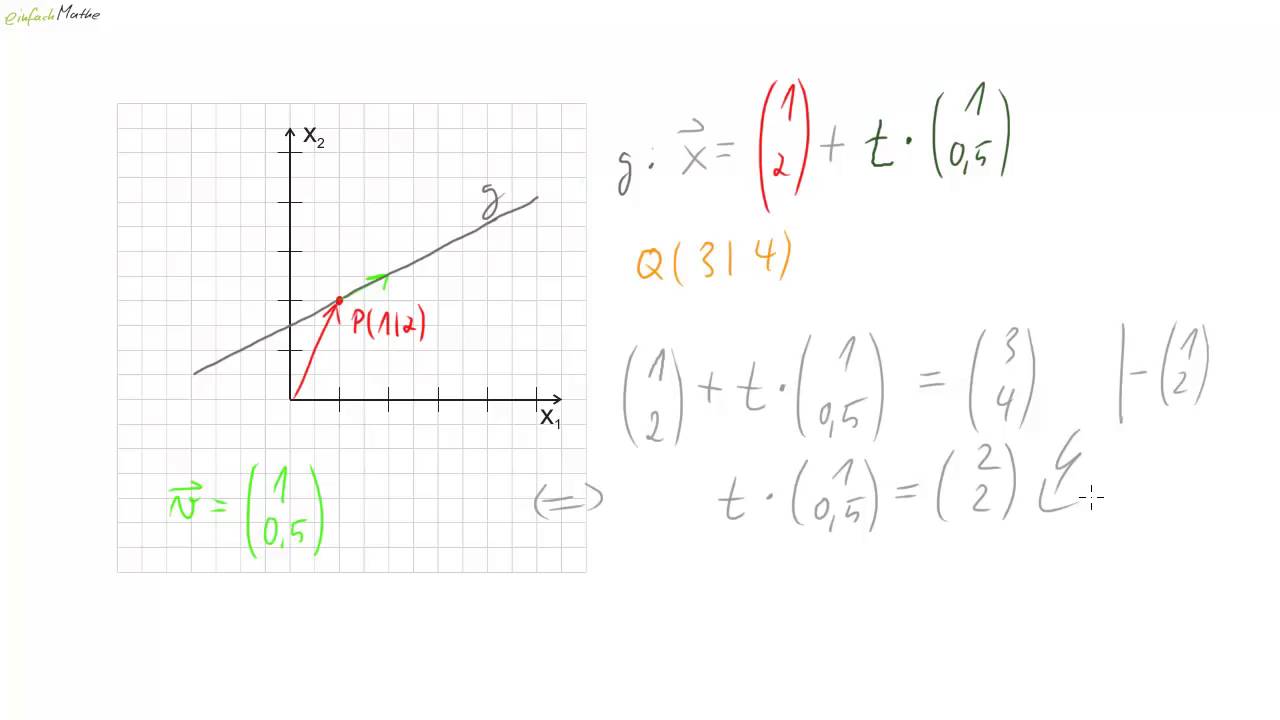überprüfen Ob Ein Punkt Auf Einer Geraden Liegt

Hast du dich jemals gefragt, ob ein Punkt genau auf einer Linie liegt, wie ein winziger Akrobat, der perfekt balanciert? Klingt vielleicht nach trockenem Mathe, aber glaub mir, das Überprüfen, ob ein Punkt auf einer Geraden liegt, ist überraschend nützlich und sogar ein bisschen cool! Denk an Computerspiele, Grafikdesign oder sogar die Navigation – überall, wo Präzision und Ausrichtung wichtig sind, spielt diese simple Berechnung eine Rolle.

Der Zweck dieser Übung ist ganz einfach: Wir wollen feststellen, ob die Koordinaten eines gegebenen Punktes die Gleichung einer bestimmten Geraden erfüllen. Mit anderen Worten: Passt der Punkt perfekt auf die Linie, oder liegt er knapp daneben? Der Nutzen davon ist vielfältig. Stell dir vor, du programmierst ein Spiel und möchtest sicherstellen, dass ein Laserstrahl genau ein Ziel trifft. Oder du entwirfst eine App, die automatisch Abstände misst und sicherstellen muss, dass die Messpunkte korrekt liegen. Die Möglichkeiten sind endlos!

Okay, wie machen wir das Ganze? Keine Sorge, es ist einfacher als du denkst. Zuerst brauchen wir die Gleichung der Geraden. Die häufigste Form ist die sogenannte Steigungs-Achsenabschnittsform: y = mx + b. Hierbei ist m die Steigung der Geraden (wie steil sie ansteigt) und b der y-Achsenabschnitt (wo die Gerade die y-Achse schneidet).

Nehmen wir an, wir haben die Gerade y = 2x + 1. Das bedeutet, die Steigung ist 2 und der y-Achsenabschnitt ist 1. Jetzt haben wir einen Punkt, sagen wir (2, 5). Um zu überprüfen, ob dieser Punkt auf der Geraden liegt, setzen wir einfach die x- und y-Koordinaten des Punktes in die Geradengleichung ein.

Also: 5 = 2 * 2 + 1

Rechnen wir das aus: 5 = 4 + 1

5 = 5

Bingo! Die Gleichung stimmt. Das bedeutet, der Punkt (2, 5) liegt genau auf der Geraden y = 2x + 1.

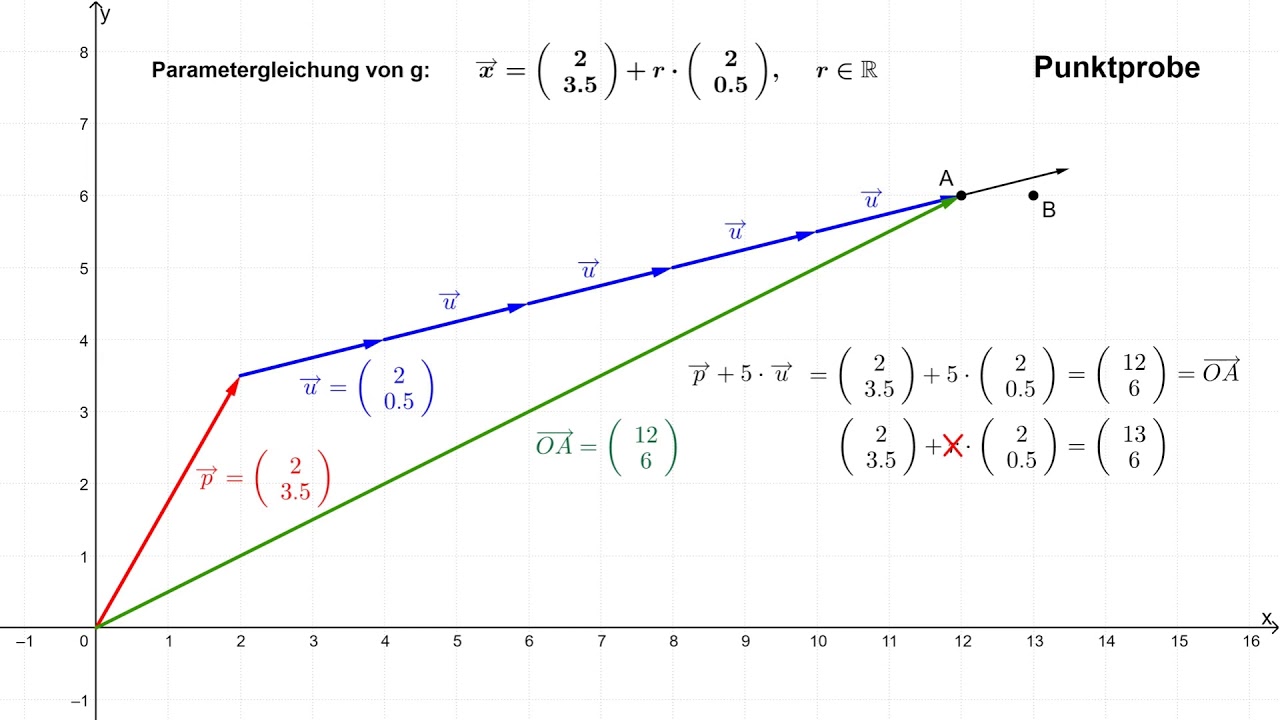
Was passiert, wenn die Gleichung nicht stimmt? Nehmen wir an, wir hätten den Punkt (1, 3).

Dann wäre die Rechnung: 3 = 2 * 1 + 1

3 = 2 + 1

3 = 3.

Ups! Warte! Nehmen wir an, wir hätten den Punkt (1, 4) statt (1, 3).

Dann wäre die Rechnung: 4 = 2 * 1 + 1

4 = 2 + 1

4 = 3

Die Gleichung stimmt nicht! Das bedeutet, der Punkt (1, 4) liegt nicht auf der Geraden. Er liegt entweder oberhalb oder unterhalb der Linie.

Das ist alles! Mit dieser einfachen Methode kannst du überprüfen, ob ein Punkt auf einer Geraden liegt. Probier es mit verschiedenen Geraden und Punkten aus. Du wirst sehen, es macht sogar Spaß! Und wer weiß, vielleicht rettest du eines Tages mit diesem Wissen die Welt (oder zumindest ein Computerspiel).