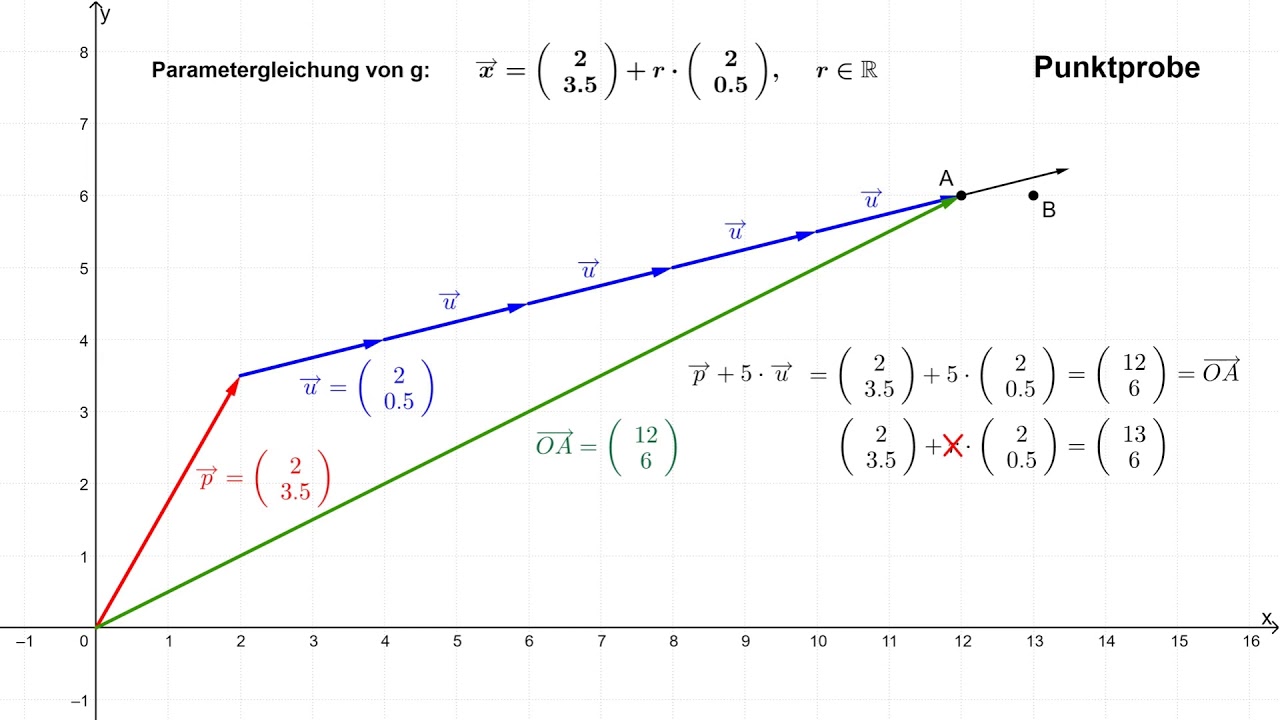
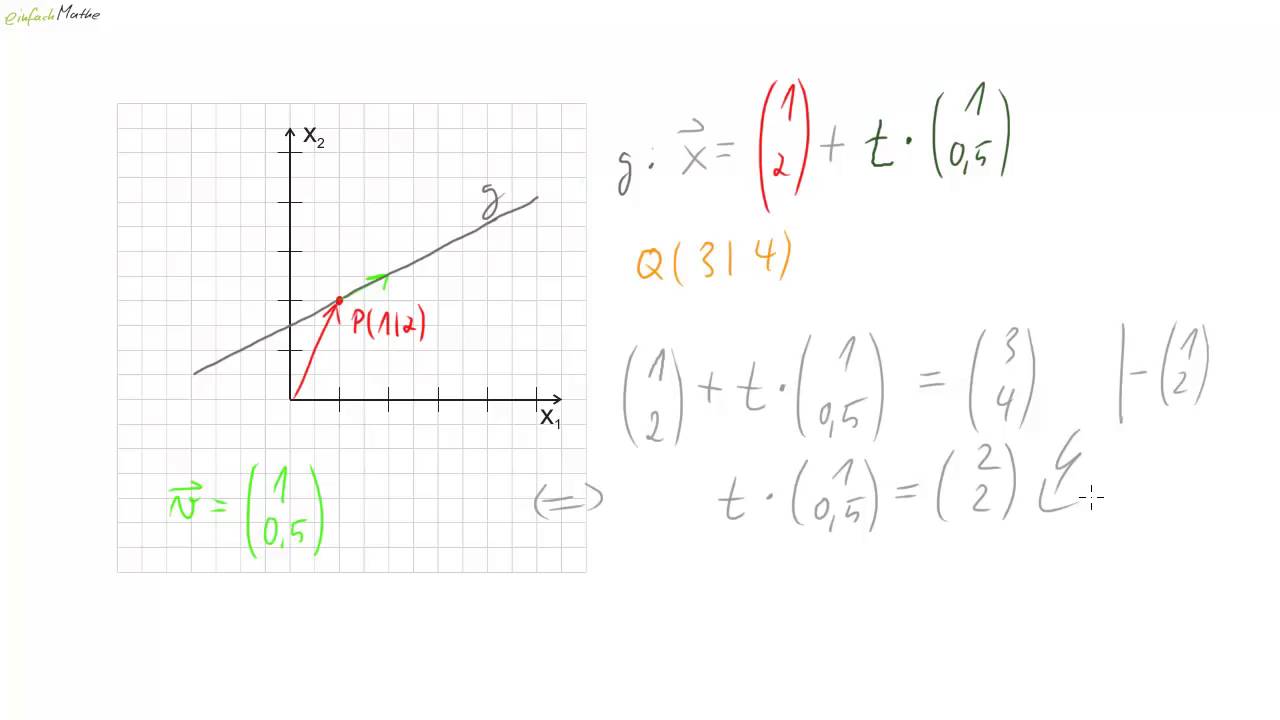überprüfen Ob Punkte Auf Einer Geraden Liegen Vektoren

Hey du! Lust auf ein kleines Gehirn-Jogging? Wir reden heute über was richtig Cooles: Vektoren! Und zwar, wie man checkt, ob Punkte brav auf einer Linie chillen, mit Hilfe dieser Dinger.

Klingt erstmal kompliziert, oder? Aber keine Panik! Das ist easy peasy. Stell dir vor, Vektoren sind wie Pfeile. Sie zeigen in eine Richtung und haben 'ne bestimmte Länge. Und diese Pfeile helfen uns, Geraden zu zähmen!

Geradeaus denken (oder Vektoriell?)

Also, du hast drei Punkte. Sagen wir, A, B und C. Deine Mission: herausfinden, ob die alle auf derselben Geraden liegen. Klingt nach 'ner Aufgabe für Sherlock Holmes, aber wir haben Vektoren!

Der Trick ist, Vektoren zwischen den Punkten zu bilden. Mach einen Vektor von A nach B, und einen von A nach C. Nennen wir die AB und AC.

Wichtig: Wenn A, B und C auf einer Geraden liegen, dann müssen diese beiden Vektoren irgendwie "parallel" sein. Aber was heißt das genau?

Parallelität bedeutet hier, dass einer der Vektoren ein Vielfaches des anderen ist. Klingt kompliziert? Denk an Skalierung! Stell dir vor, du nimmst den AB-Vektor und ziehst ihn entweder auseinander oder stauchst ihn zusammen. Wenn du das so machen kannst, dass er genau wie der AC-Vektor aussieht, bingo! Die Punkte liegen auf einer Geraden.

Mathematisch ausgedrückt: AB = k * AC, wobei k eine Zahl ist (die wir Skalar nennen). K kann jede reelle Zahl sein – positiv, negativ, sogar ein Bruch!

Das Koordinaten-Chaos (aber auf eine gute Art!)

Okay, genug der Theorie. Wie machen wir das konkret? Nun, jeder Punkt hat Koordinaten. Sagen wir, A ist (x1, y1), B ist (x2, y2) und C ist (x3, y3).

Um den AB-Vektor zu finden, ziehst du einfach die Koordinaten von A von denen von B ab: AB = (x2 - x1, y2 - y1). Genauso für AC: AC = (x3 - x1, y3 - y1).

Jetzt kommt der spannende Teil: Du willst prüfen, ob (x2 - x1, y2 - y1) = k * (x3 - x1, y3 - y1) für irgendein k gilt. Das bedeutet, dass (x2 - x1) = k * (x3 - x1) *UND* (y2 - y1) = k * (y3 - y1) sein muss.

Wenn du ein k findest, das *beide* Gleichungen erfüllt, dann hast du gewonnen! Die Punkte liegen auf einer Linie. Wenn nicht… nun ja, dann tanzen sie halt woanders rum.

Kleiner Tipp: Oft ist es am einfachsten, *zuerst* zu versuchen, k aus einer der Gleichungen zu bestimmen (z.B. k = (x2 - x1) / (x3 - x1)) und dann zu prüfen, ob dieses k auch die andere Gleichung erfüllt. Aber Achtung, was, wenn (x3 - x1) Null ist?!

Der Null-Divisions-Albtraum (und wie man ihn vermeidet)

Ja, was, wenn (x3 - x1) = 0 ist? Dann hast du ein Problem. Man darf nicht durch Null teilen! Aber keine Sorge, es gibt eine Lösung: Prüfe, ob *auch* (x2 - x1) = 0 ist. Wenn beides Null ist, dann sind die x-Koordinaten von A, B und C gleich. Das bedeutet, die Punkte liegen auf einer vertikalen Linie!

Wenn (x3 - x1) = 0, aber (x2 - x1) != 0, dann liegen die Punkte *nicht* auf einer Geraden.

Merke: Sei vorsichtig mit Null-Divisionen! Sie sind die kleinen Teufel der Mathematik.

Warum ist das überhaupt wichtig?

Okay, okay, das ist alles ganz nett, aber wofür braucht man das im echten Leben? Gute Frage! Nun, das Konzept taucht überall auf, wo es um Geometrie, Computergrafik oder sogar Physik geht.

Denk an Computerspiele! Wenn du eine gerade Linie zwischen zwei Punkten ziehen willst, muss der Computer wissen, welche Pixel er "anmalen" muss. Und dabei spielen Vektoren eine Rolle.

Oder denk an Navigation. Wenn du mit dem Auto fährst, berechnet dein Navi ständig die kürzeste Route. Und diese Routen bestehen oft aus geraden Linien.

Und ganz ehrlich? Es ist einfach cool zu wissen, wie man solche Probleme lösen kann. Man fühlt sich ein bisschen wie ein Mathe-Ninja!

Fazit: Vektoren sind deine Freunde!

Also, da hast du's! Punkte auf einer Geraden prüfen mit Vektoren ist gar nicht so schwer. Es braucht ein bisschen Übung, aber mit der Zeit wirst du zum Vektor-Profi.

Und denk dran: Mathe muss nicht langweilig sein. Es kann auch Spaß machen! Also, geh raus, spiel mit Vektoren und entdecke die Welt der Geometrie!

P.S. Wenn du noch mehr wissen willst, google mal nach "kollineare Punkte". Da findest du tonnenweise Infos und Beispiele. Viel Spaß!