überprüfen Sie Ob Das Viereck Abcd Ein Parallelogramm Ist

Hey Leute! Habt ihr euch jemals gefragt, wie man eigentlich *ganz sicher* feststellt, ob ein Viereck ein Parallelogramm ist? Klar, man kann's mit den Augen abschätzen. Aber was, wenn das Viereck ein bisschen schief gezeichnet ist, oder man einfach nicht so gut im Schätzen ist? Keine Sorge, dafür gibt's ein paar coole Tricks!
Stellt euch vor, ein Parallelogramm ist wie ein sehr disziplinierter Tänzer. Alles ist parallel und koordiniert. Die gegenüberliegenden Seiten gehen im Gleichschritt, die Winkel sind harmonisch aufeinander abgestimmt. Aber wie finden wir heraus, ob unser Viereck wirklich so gut tanzt?
Die Seiten: Parallelität ist Trumpf
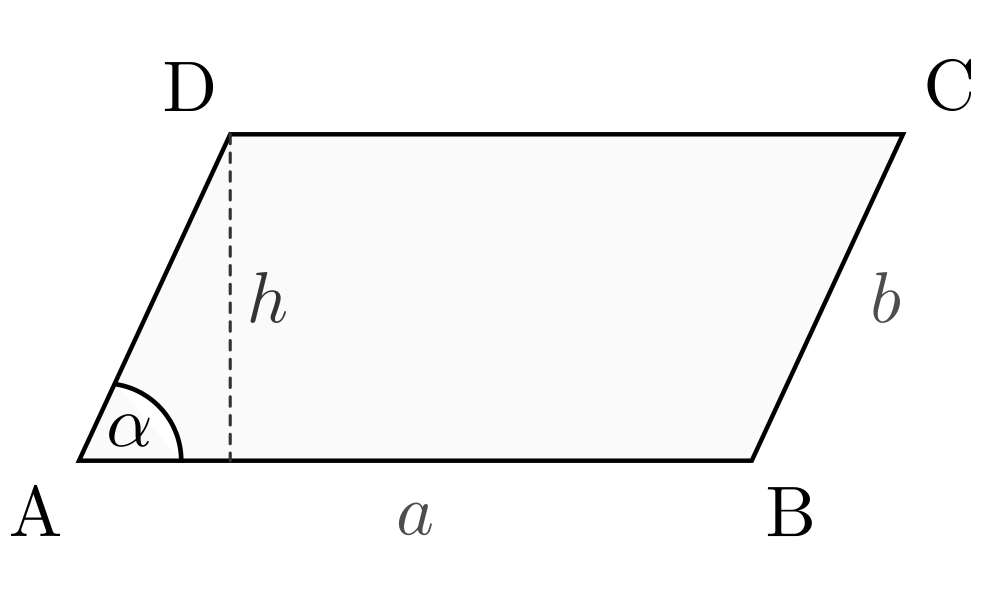
Die erste und vielleicht offensichtlichste Eigenschaft eines Parallelogramms ist, dass die gegenüberliegenden Seiten parallel sind. Parallelität... Klingt irgendwie nach einem Science-Fiction-Film, oder? Aber im Grunde bedeutet es nur, dass die Seiten sich niemals treffen, egal wie weit man sie verlängert. Wie Gleise einer Eisenbahn, die (hoffentlich!) niemals zusammenkommen.
Also, wie überprüfen wir das? Nun, in der Schule lernt man das mit Winkeln an geschnittenen Geraden. Wenn man so etwas zur Hand hat (Zirkel, Geodreieck) prima! Aber die einfachste Methode ist... messen! Wenn du die gegenüberliegenden Seiten misst und feststellst, dass sie gleich lang sind *und* parallel (oder das zumindest sehr, sehr nah dran ist), dann hast du schon einen guten Hinweis. Sind aber *nur* die Seiten gleich lang, aber nicht parallel, dann hast du vielleicht eher ein Drachenviereck!
Denkt dran: Gleich lang *und* parallel. Doppelt hält besser, oder?
Die Winkel: Gegenüberliegend und Ergänzend
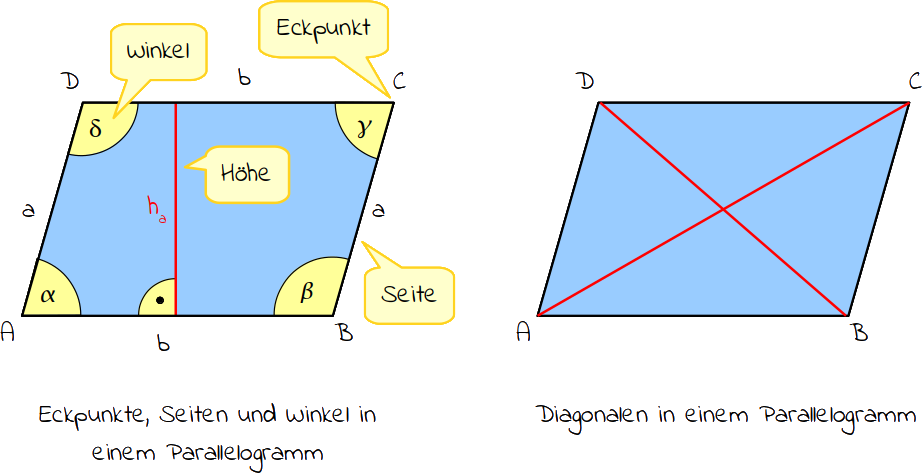
Okay, die Seiten haben wir gecheckt. Aber was ist mit den Winkeln? Auch hier gibt's eine coole Regel: Die gegenüberliegenden Winkel in einem Parallelogramm sind gleich groß. Also der Winkel oben links muss genauso groß sein wie der Winkel unten rechts, und der Winkel oben rechts muss genauso groß sein wie der Winkel unten links. Stellt euch vor, sie sind wie Zwillinge!
Und es kommt noch besser: Die nebeneinanderliegenden Winkel (also z.B. der Winkel oben links und der Winkel oben rechts) sind ergänzend. Das bedeutet, sie ergeben zusammen 180 Grad. Wie zwei Puzzleteile, die perfekt zusammenpassen, um eine gerade Linie zu bilden.
Wenn diese Winkel-Beziehungen stimmen, dann sieht es schon sehr gut aus für unser Viereck. Aber Achtung: Auch hier gilt, dass *beide* Bedingungen (gleich gegenüberliegende Winkel *und* ergänzende benachbarte Winkel) erfüllt sein müssen, um sicher zu sein.
Die Diagonalen: Halbierung als Indiz
Jetzt wird's ein bisschen trickreicher, aber keine Angst, wir kriegen das hin! Die Diagonalen in einem Parallelogramm haben eine besondere Eigenschaft: Sie halbieren sich gegenseitig. Das bedeutet, dass der Schnittpunkt der Diagonalen genau in der Mitte jeder Diagonale liegt.
Stellt euch die Diagonalen wie zwei Stöcke vor, die sich in der Mitte kreuzen. Wenn der Kreuzungspunkt genau in der Mitte beider Stöcke liegt, dann habt ihr gute Chancen, dass ihr ein Parallelogramm vor euch habt. Aber wenn einer der Stöcke "aus dem Gleichgewicht" ist, dann eher nicht.
Um das zu überprüfen, müsst ihr die Diagonalen messen und den Schnittpunkt finden. Dann messt ihr die Strecken vom Schnittpunkt zu den Endpunkten der Diagonalen. Sind die Strecken auf jeder Diagonale gleich lang? Perfekt! Das ist ein starkes Indiz für ein Parallelogramm.
Fazit: Mehrere Wege führen zum Parallelogramm
Es gibt also mehrere Möglichkeiten, um herauszufinden, ob ein Viereck ein Parallelogramm ist. Man kann sich auf die Seiten konzentrieren (sind die gegenüberliegenden Seiten gleich lang und parallel?), auf die Winkel (sind die gegenüberliegenden Winkel gleich und die benachbarten Winkel ergänzend?) oder auf die Diagonalen (halbieren sie sich gegenseitig?).
Am sichersten ist es, *mehrere* dieser Eigenschaften zu überprüfen. Wenn alle oder die meisten Kriterien erfüllt sind, dann könnt ihr euch ziemlich sicher sein, dass euer Viereck tatsächlich ein Parallelogramm ist. Und wenn nicht? Dann habt ihr zumindest etwas gelernt! Viel Spaß beim Ausprobieren!
Und denkt dran: Geometrie muss nicht langweilig sein! Seht es als ein Spiel, ein Rätsel, das gelöst werden will. Und wer weiß, vielleicht entdeckt ihr ja eure Leidenschaft für Formen und Winkel!