Unter Welchem Winkel Schneidet Der Graph Die Y Achse

Hey du! Hast du dich jemals gefragt, wie genau eine Kurve die Y-Achse schneidet? Klingt erstmal nach trockenem Mathe, aber keine Sorge, wir machen's spannend! Stell dir vor, du bist ein Designer von Achterbahnen oder ein Architekt, der Brücken entwirft. Zu wissen, unter welchem Winkel etwas eine Achse schneidet, ist super wichtig, um sicherzustellen, dass alles reibungslos und sicher läuft. Aber auch für den Alltag kann das Verständnis helfen, Diagramme und Grafiken besser zu interpretieren. Also, los geht's – wir tauchen ein in die Welt der Schnittwinkel mit der Y-Achse!
Warum ist das Ganze überhaupt nützlich? Nun, der Schnittwinkel gibt uns wertvolle Informationen über das Verhalten einer Funktion an einem bestimmten Punkt. Er verrät uns, wie steil die Kurve gerade an dieser Stelle ist. In der Physik hilft uns das, die Geschwindigkeit eines Objekts zu bestimmen, wenn die Funktion beispielsweise die Position über die Zeit darstellt. In der Wirtschaft können wir damit die Änderungsrate von Verkaufszahlen oder Aktienkursen analysieren. Kurz gesagt: Der Schnittwinkel ist ein wichtiges Werkzeug, um Trends und Veränderungen zu verstehen.
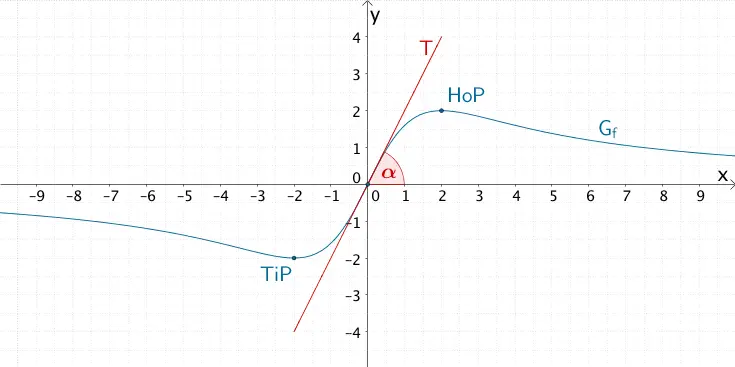
Wie finden wir diesen Winkel denn heraus? Das Zauberwort heißt Ableitung! Ja, ich weiß, das klingt erstmal kompliziert, aber keine Panik. Die Ableitung einer Funktion an einem bestimmten Punkt gibt uns die Steigung der Tangente an die Kurve genau an diesem Punkt. Die Tangente ist im Prinzip eine gerade Linie, die die Kurve in diesem Punkt berührt. Und die Steigung dieser Tangente ist eng mit dem Schnittwinkel verbunden.
Konkret geht das so: Zuerst ermitteln wir den Punkt, an dem die Funktion die Y-Achse schneidet. Dieser Punkt hat die Koordinaten (0, y). Das ist wichtig! Dann bilden wir die Ableitung der Funktion. Die Ableitung, oft mit f'(x) bezeichnet, gibt uns die Steigung für jeden beliebigen x-Wert. Nun setzen wir x = 0 in die Ableitung ein. Das Ergebnis, f'(0), ist die Steigung der Tangente an die Kurve im Schnittpunkt mit der Y-Achse. Nennen wir diese Steigung 'm'.
Und jetzt kommt der Clou: Der Winkel α (Alpha) zwischen der Tangente und der Y-Achse lässt sich mit folgender Formel berechnen: tan(α) = 1/m, wobei 'm' die Steigung ist, die wir gerade berechnet haben. Um den Winkel selbst zu erhalten, brauchst du den Arkustangens (arctan) oder tan-1. Das heißt: α = arctan(1/m). Keine Sorge, dein Taschenrechner kann das! Stell ihn aber unbedingt auf Gradmaß (DEG) ein, damit du das Ergebnis in Grad erhältst.
Ein kurzes Beispiel: Nehmen wir an, unsere Funktion ist f(x) = x2 + 2x + 1. Die Ableitung ist f'(x) = 2x + 2. Der Schnittpunkt mit der Y-Achse ist (0, 1). Wir setzen x = 0 in die Ableitung ein: f'(0) = 2. Also ist die Steigung m = 2. Jetzt berechnen wir den Winkel: α = arctan(1/2) ≈ 26,57°. Das bedeutet, die Kurve schneidet die Y-Achse unter einem Winkel von ungefähr 26,57 Grad.
Na, siehst du? Gar nicht so schwer, oder? Mit ein bisschen Übung und dem richtigen Taschenrechner wirst du zum Schnittwinkel-Meister! Und denk dran: Mathematik kann auch Spaß machen, besonders wenn man sieht, wie sie uns hilft, die Welt um uns herum besser zu verstehen.