Verhalten Im Unendlichen Ganzrationale Funktionen
Stell dir vor, du bist auf einer Achterbahn. Nicht irgendeine Achterbahn, sondern die verrückteste, längste, höchste Achterbahn der Welt! Die Fahrt geht ewig weiter, ins Unendliche sozusagen! Aber was passiert ganz am Ende? Wohin geht die Reise, wenn wir diese Achterbahn unendlich lange fahren?
Genau darum geht's beim "Verhalten im Unendlichen" von ganzrationalen Funktionen. Klingt kompliziert? Ist es aber gar nicht! Ganzrationale Funktionen, das sind im Grunde nur nette, einfache Gleichungen, die wir in Schaubildern darstellen können. Denk an sowas wie y = x + 2 oder y = x² - 3x + 1. Keine Angst, wir brauchen keine komplizierten Formeln. Stell dir einfach vor, jede dieser Gleichungen malt eine Kurve auf einem Blatt Papier – unsere Achterbahn!
Die Frage aller Fragen: Wohin geht's?
Wenn wir uns diese Achterbahnen (also die Schaubilder) ganz genau ansehen, stellen wir fest: Irgendwann haben sie eine Tendenz. Entweder sie sausen immer weiter nach oben (ins positive Unendliche) oder sie stürzen immer tiefer ab (ins negative Unendliche). Und genau das ist das "Verhalten im Unendlichen": Wir wollen wissen, wohin die Reise geht, wenn x (also unser Platz auf der Achterbahn) immer größer (positiv unendlich) oder immer kleiner (negativ unendlich) wird.
Der Leithammel: Der höchste Exponent
Das Geheimnis, um das Verhalten im Unendlichen zu entschlüsseln, liegt in der Potenz mit dem höchsten Exponenten. Denk an y = 5x3 + 2x2 - x + 7. Hier ist die 3 die höchste Potenz (x3). Dieser Teil der Gleichung ist wie der Kapitän der Achterbahn. Er bestimmt, wohin es am Ende geht. Die anderen Teile der Gleichung (2x2, -x, +7) sind zwar auch da, aber sie haben nicht genug Power, um den Kurs zu ändern. Sie sind wie kleine Kinder, die versuchen, ein riesiges Containerschiff umzulenken – keine Chance!
Also, was macht der Kapitän? Das hängt von zwei Dingen ab:
- Ist der Exponent gerade oder ungerade? Stell dir vor, gerade ist wie eine U-Bahn: egal in welche Richtung (positiv oder negativ), sie fährt immer in eine Röhre (entweder nach oben oder nach unten). Ungerade ist wie eine Rutsche: eine Richtung hoch, die andere runter.
- Ist der Vorfaktor positiv oder negativ? Positiv bedeutet: "Juhu, nach oben!". Negativ bedeutet: "Achtung, es geht abwärts!".
Beispiele, Beispiele, Beispiele!
Okay, genug Theorie, jetzt wird's anschaulich!
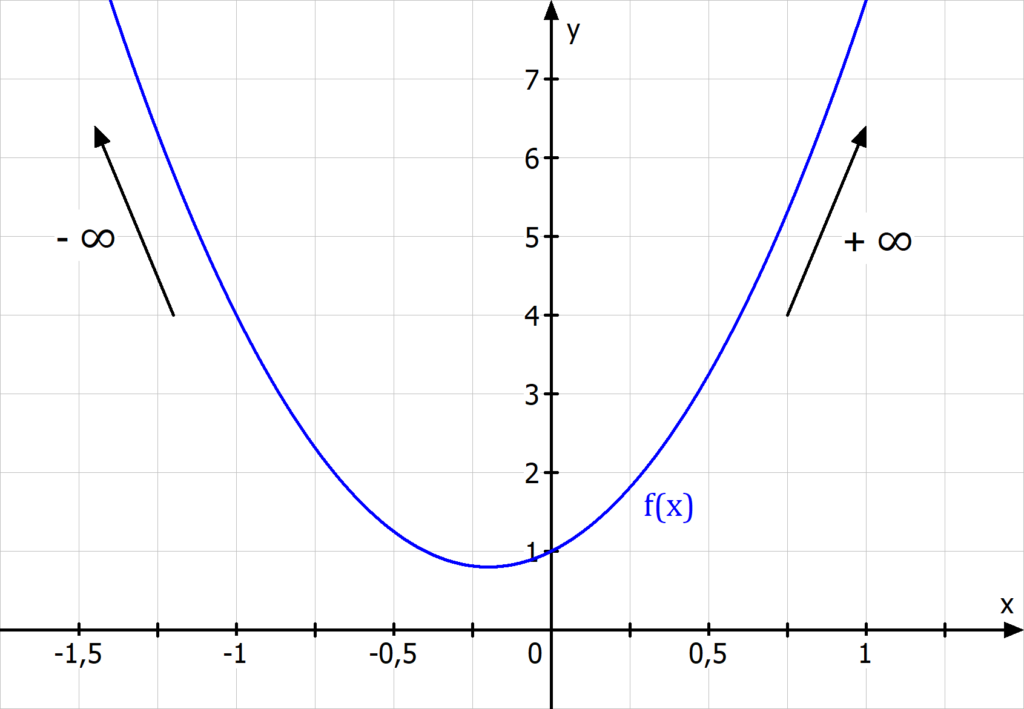
Beispiel 1: y = 2x2 + x - 1. Der höchste Exponent ist 2 (gerade), der Vorfaktor ist 2 (positiv). Das bedeutet: Die Achterbahn fährt nach oben, egal ob wir nach vorne oder nach hinten fahren! Sowohl im positiven als auch im negativen Unendlichen geht's Richtung Himmel.
Beispiel 2: y = -3x3 + x2 + 5. Der höchste Exponent ist 3 (ungerade), der Vorfaktor ist -3 (negativ). Das bedeutet: Wenn wir nach vorne fahren (positiv unendlich), geht's abwärts. Wenn wir nach hinten fahren (negativ unendlich), geht's aufwärts! Eine echte Adrenalin-Achterbahn!
Beispiel 3: y = x4 - 7x2 + 3. Der höchste Exponent ist 4 (gerade), der Vorfaktor ist 1 (positiv). Hier geht's wieder in beide Richtungen nach oben, aber diesmal mit noch mehr Schwung!
Wichtig: Es geht nur um die Tendenz. Die Achterbahn kann zwischendurch Zickzack fahren oder Loopings drehen. Aber am Ende zählt nur: Wohin geht die Reise, wenn wir unendlich weit fahren?
Fazit: Keine Angst vor dem Unendlichen!
Das Verhalten im Unendlichen von ganzrationalen Funktionen ist also gar nicht so gruselig, wie es klingt. Es ist wie eine Wettervorhersage für Achterbahnen. Wir können voraussagen, ob es am Ende hoch oder runter geht, ohne die ganze Strecke abzufahren. Und das ist doch ziemlich cool, oder?
Also, das nächste Mal, wenn du eine ganzrationale Funktion siehst, denk an eine Achterbahnfahrt und frag dich: Wohin geht's im Unendlichen? Du wirst überrascht sein, wie einfach das zu beantworten ist! Und wer weiß, vielleicht wirst du ja auch zum Achterbahn-Vorhersage-Experten!