Was Ist Der Unterschied Zwischen Reellen Und Rationalen Zahlen
Hey du! Zahlen, Zahlen, überall? Finden wir's heraus! Was ist eigentlich der Unterschied zwischen reellen und rationalen Zahlen? Klingt kompliziert? Keine Sorge, wird's nicht!
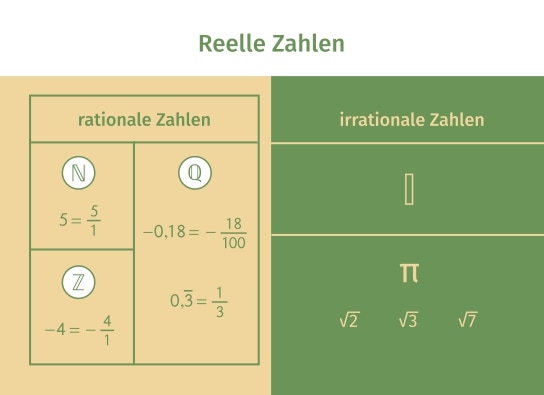
Rationale Zahlen: Die Ordentlichen unter uns
Stell dir vor, die rationalen Zahlen sind super ordentlich. Sie lieben Brüche! Ja, genau. Alles, was du als Bruch darstellen kannst, ist rational. Zum Beispiel 1/2, 3/4, oder sogar -5/7.
Aber Achtung: Ganze Zahlen gehören auch dazu! Warum? Weil du jede ganze Zahl auch als Bruch schreiben kannst. Zum Beispiel ist 5 das Gleiche wie 5/1. Bingo!
Was ist noch rational? Dezimalzahlen, die irgendwann aufhören (z.B. 0.25) oder sich wiederholen (z.B. 0.333...). Diese kann man nämlich auch als Brüche darstellen. Clever, oder?
Denk an Pizza. Eine halbe Pizza (1/2) ist super rational. Eine Viertelpizza (1/4) auch! Solange du sie in gleichmäßige Stücke schneiden kannst, ist alles gut.
Merke: Rationale Zahlen sind wie ordentliche kleine Päckchen, die wir leicht verstehen und handhaben können.
Reelle Zahlen: Die Wilden und Unberechenbaren
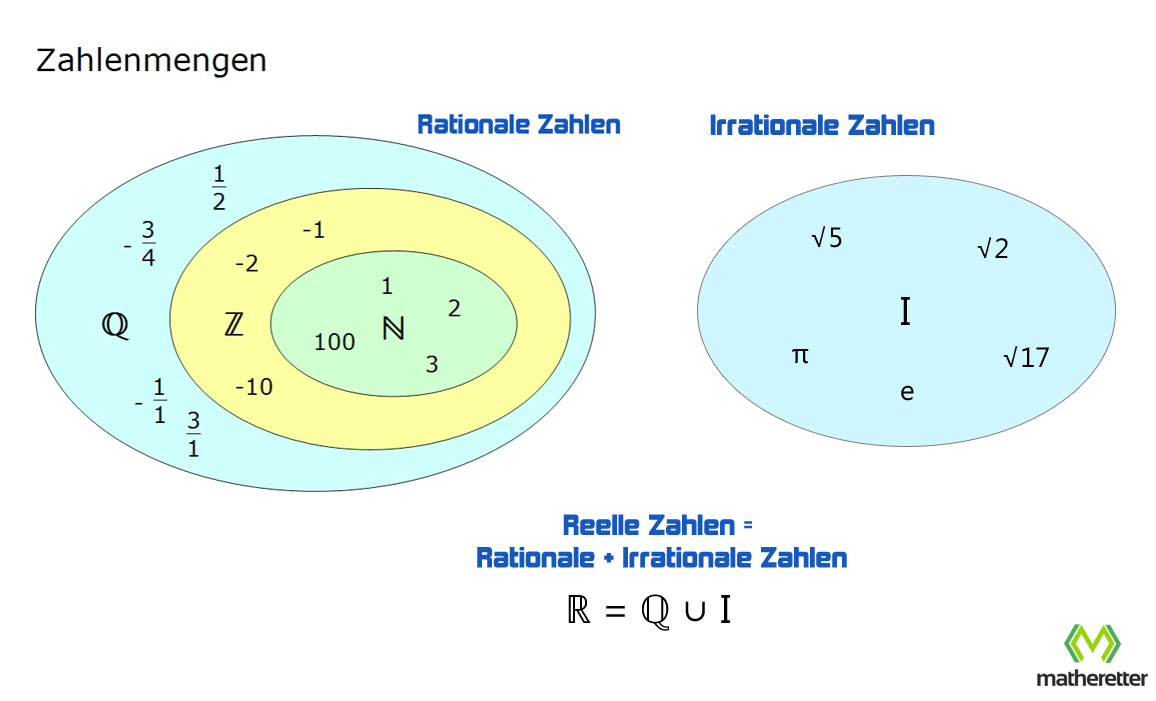
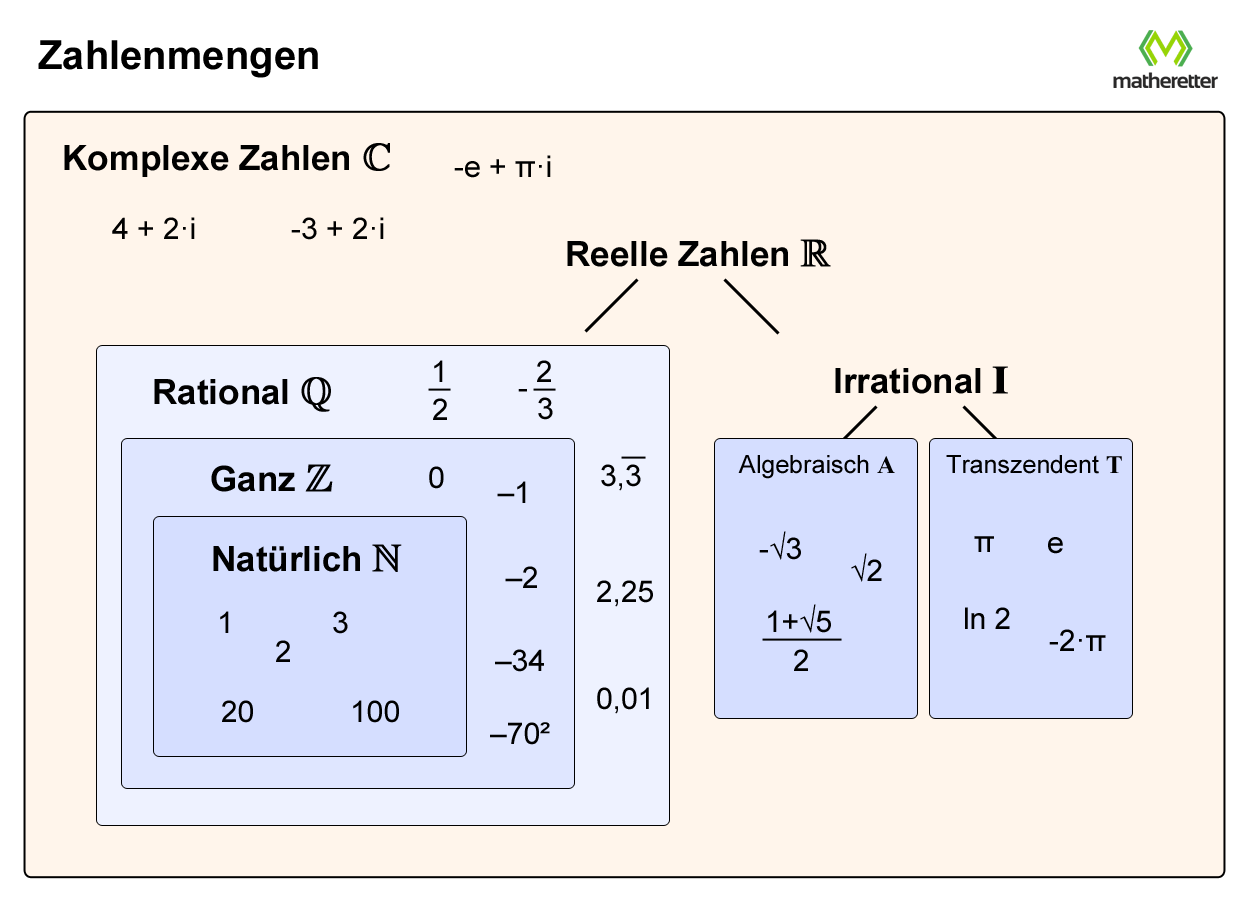
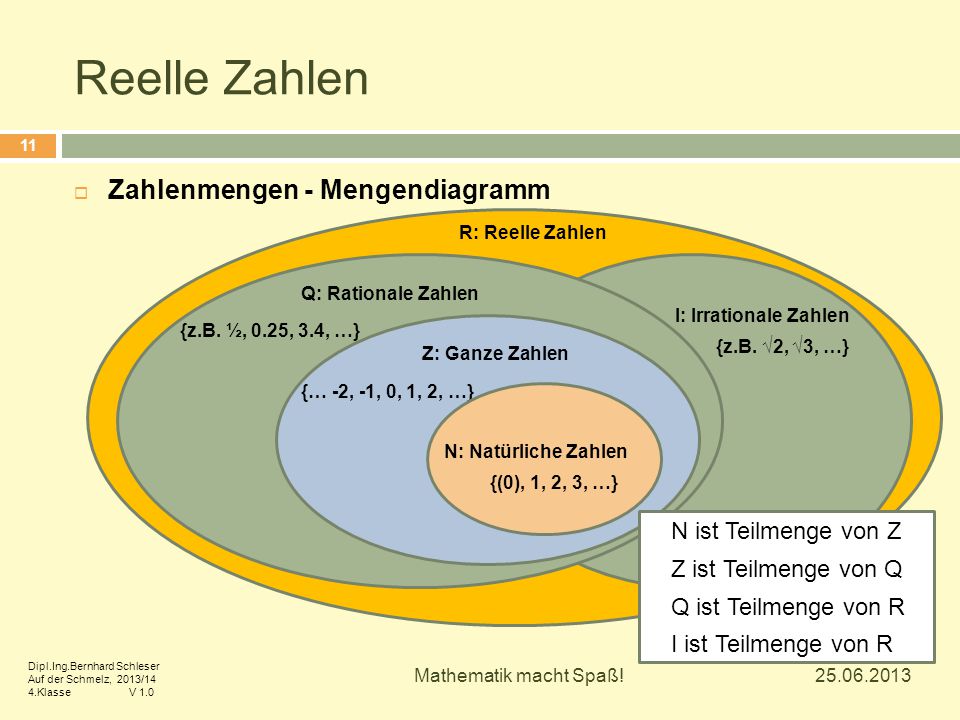
Jetzt kommen die reellen Zahlen ins Spiel! Das sind sozusagen alle Zahlen, die du dir vorstellen kannst. Rationale Zahlen sind natürlich auch dabei. Aber es gibt da noch was...
Die irrationalen Zahlen! Das sind die wilden Kerle unter den Zahlen. Sie sind reell, aber nicht rational. Was bedeutet das?
Sie lassen sich nicht als Bruch darstellen! Und ihre Dezimaldarstellung ist endlos und wiederholt sich nicht. Chaos pur!
Denk an Pi (π). 3.14159... und so weiter, bis in die Unendlichkeit. Keine Wiederholung, kein Ende. Verrückt, oder? Das ist eine typische irrationale Zahl.
Oder die Wurzel aus 2 (√2). Ungefähr 1.41421... Auch hier: Endlos und ohne Muster. Irrational! (Und super hilfreich beim Bauen von rechtwinkligen Dreiecken, aber das ist eine andere Geschichte).
Stell dir vor, du versuchst, Pi in gleichmäßige Pizzastücke zu schneiden. Unmöglich! Es geht einfach nicht auf. Das ist der Unterschied: Rationale Zahlen lassen sich ordentlich teilen, irrationale nicht.
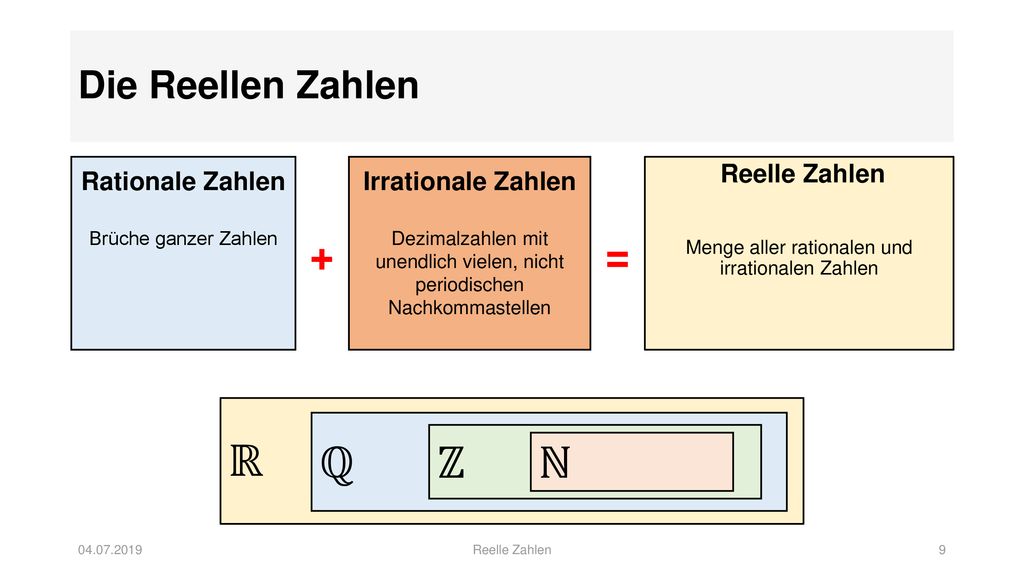
Merke: Reelle Zahlen umfassen alles. Rationale und Irrationale. Sie sind wie das gesamte Universum der Zahlen.
Der Unterschied auf den Punkt gebracht
Also, was ist der große Unterschied?
- Rationale Zahlen: Sind Brüche (oder lassen sich als Brüche darstellen). Ihre Dezimaldarstellung endet oder wiederholt sich. Ordentlich und berechenbar.
- Reelle Zahlen: Umfassen alle Zahlen, rational und irrational. Irrationale Zahlen lassen sich nicht als Brüche darstellen. Ihre Dezimaldarstellung ist endlos und wiederholt sich nicht. Wild und unberechenbar.
Vereinfacht gesagt: Alle rationalen Zahlen sind reell, aber nicht alle reellen Zahlen sind rational.
Warum ist das wichtig?
Gute Frage! Im Alltag begegnen wir oft rationalen Zahlen. Beim Abmessen von Zutaten, beim Bezahlen im Supermarkt... Rationale Zahlen sind praktisch und handlich.
Aber reelle Zahlen sind auch wichtig! In der Mathematik, der Physik und der Ingenieurwissenschaft spielen irrationale Zahlen eine entscheidende Rolle. Sie beschreiben komplexe Zusammenhänge, die mit rationalen Zahlen allein nicht darstellbar wären.
Denk an die Berechnung von Kreisflächen (π) oder an die Bewegung von Planeten. Ohne irrationale Zahlen wäre das Universum ein viel einfacheres (und langweiligeres) Ort!
Fazit: Zahlen sind cool!
Also, jetzt weißt du Bescheid! Der Unterschied zwischen reellen und rationalen Zahlen ist gar nicht so kompliziert, oder? Es geht einfach darum, ob eine Zahl sich als Bruch darstellen lässt oder nicht.
Und mal ehrlich: Zahlen sind doch total faszinierend! Sie beschreiben die Welt um uns herum und helfen uns, sie zu verstehen. Ob rational oder irrational, jede Zahl hat ihre eigene kleine Geschichte zu erzählen.
Also, geh raus und entdecke die Welt der Zahlen! Vielleicht findest du ja sogar deine eigene Lieblingszahl. Und wer weiß, vielleicht ist sie ja sogar irrational! 😉