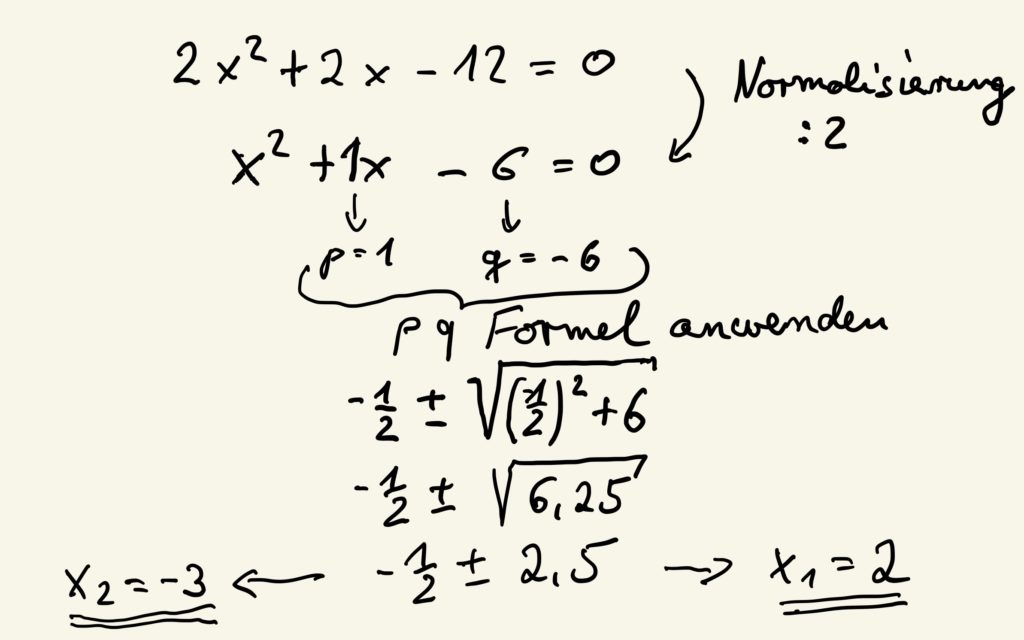Was Rechnet Man Mit Der Pq Formel Aus

Hey Mathe-Muffel und Zahlen-Zahmer! Habt ihr euch jemals gefragt, wie man diese berühmte Formel anwendet, die in Mathebüchern lauert und auf den ersten Blick so kompliziert aussieht? Keine Sorge, wir tauchen heute gemeinsam ein in die Welt der p-q-Formel und entdecken, warum sie gar nicht so gruselig ist, wie sie scheint. Stellt euch vor, ihr knackt einen Code, der euch hilft, wichtige mathematische Probleme zu lösen! Das ist der Reiz der p-q-Formel.
Also, was genau rechnet man mit der p-q-Formel aus? Kurz gesagt: Sie hilft uns, die Nullstellen einer quadratischen Gleichung zu finden. Quadratische Gleichungen sind Gleichungen der Form x² + px + q = 0. Diese Gleichungen beschreiben viele reale Phänomene, von der Flugbahn eines Balls bis hin zur Optimierung von Geschäftsprozessen. Und die Nullstellen? Das sind die Werte für x, die die Gleichung zu Null machen. Stell dir vor, du suchst die Punkte, an denen eine Parabel die x-Achse schneidet – das sind die Nullstellen!
Die p-q-Formel lautet: x1,2 = -p/2 ± √( (p/2)² - q ). Klingt kompliziert? Lass uns das aufdröseln! p und q sind einfach die Koeffizienten (Zahlen) vor den x-Termen und dem konstanten Term in unserer quadratischen Gleichung. Die Formel gibt uns zwei mögliche Lösungen (daher das x1,2). Das ± bedeutet, dass wir einmal addieren und einmal subtrahieren müssen, um beide Nullstellen zu finden. Das Symbol √ steht für die Quadratwurzel.
Warum ist die p-q-Formel so nützlich? Erstens, sie ist eine direkte Methode, um Nullstellen zu berechnen. Im Gegensatz zum Ausprobieren oder Herumraten liefert sie uns die Lösung auf einen Schlag. Zweitens, sie ist allgemeingültig für quadratische Gleichungen in der Form x² + px + q = 0. Das bedeutet, sobald du deine Gleichung in diese Form gebracht hast, kannst du die Formel anwenden. Drittens, sie hilft uns zu verstehen, wie viele Lösungen eine quadratische Gleichung hat. Der Ausdruck unter der Quadratwurzel, (p/2)² - q, wird als Diskriminante bezeichnet. Ist er positiv, gibt es zwei Lösungen. Ist er null, gibt es genau eine Lösung. Ist er negativ, gibt es keine reellen Lösungen.
Stell dir vor, du bist ein Ingenieur, der eine Brücke baut. Du musst sicherstellen, dass die Brücke stabil ist und nicht unter dem Gewicht des Verkehrs zusammenbricht. Quadratische Gleichungen und die p-q-Formel können dir helfen, die optimalen Maße der Brücke zu berechnen. Oder du bist ein Wirtschaftswissenschaftler, der den Gewinn eines Unternehmens maximieren will. Mit quadratischen Funktionen und der p-q-Formel kannst du den optimalen Preis für ein Produkt finden. Die Anwendungen sind vielfältig und reichen von der Physik über die Informatik bis hin zur Wirtschaft.
Also, das nächste Mal, wenn du eine quadratische Gleichung siehst, hab keine Angst! Denk an die p-q-Formel als deinen Superhelden, der dir hilft, die Nullstellen zu finden und die Geheimnisse der Mathematik zu lüften. Übung macht den Meister – je mehr du sie anwendest, desto einfacher wird sie dir fallen. Und wer weiß, vielleicht entdeckst du ja sogar deine Liebe zur Mathematik!