Wechselwinkel Stufenwinkel Scheitelwinkel Nebenwinkel Pdf
Leute, Leute, lasst mich euch mal was erzählen! Ich saß neulich im Café, bestellte mir 'nen Latte Macchiato (mit extra viel Schaum, versteht sich) und blätterte gelangweilt in einer alten Mathe-Zeitschrift. Und da stolperte ich über… *Wechselwinkel, Stufenwinkel, Scheitelwinkel* und *Nebenwinkel*. Klingt erstmal wie 'ne Gang aus 'nem schlechten Agentenfilm, oder? Aber keine Panik, ist alles halb so wild – versprochen!
Also, stellt euch zwei schnurgerade Linien vor, die sich schneiden. So richtig mittenmang. Zack! Da entstehen vier Winkel. Und diese Winkel haben, wie in jeder guten WG, ganz bestimmte Beziehungen zueinander. Manche sind Kumpels, andere eher so der Typ, den man nur grüßt, wenn man zufällig im Aufzug steht.
Der Scheitelwinkel – Der Doppelgänger
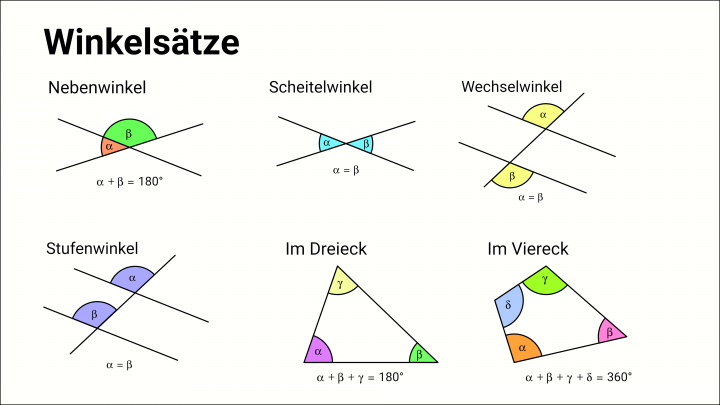
Fangen wir mit den *Scheitelwinkeln* an. Das sind die Winkel, die sich direkt gegenüberliegen. Stell dir vor, die Linien sind ein Kreuz und die Scheitelwinkel sind wie dein Spiegelbild. Sie sind absolut identisch, Zwillinge, Doppelgänger! Wenn einer 30 Grad hat, hat der andere auch 30 Grad. Keine Diskussion. Das ist Gesetz! Wer sich hier nicht einig ist, kriegt Nachsitzen bei Pythagoras.
Warum sie gleich sind? Äh… weil's so ist! Okay, Spaß beiseite. Rein mathematisch lässt sich das beweisen, aber wer will das schon an einem gemütlichen Nachmittag im Café? Vertraut mir einfach. Scheitelwinkel sind gleich. Punkt.
Der Nebenwinkel – Der Hilfsbereite
Jetzt kommen die *Nebenwinkel* ins Spiel. Die sitzen direkt nebeneinander, quasi Schulter an Schulter. Und jetzt kommt der Clou: Zusammen ergeben sie immer 180 Grad. Das ist wie bei 'ner Pizza, die in zwei Stücke geschnitten ist. Die beiden Stücke ergeben zusammen wieder die ganze Pizza, also 180 Grad. Wenn du also einen Winkel von 50 Grad hast, ist sein Nebenwinkel 130 Grad (weil 50 + 130 = 180). Praktisch, oder? So kannst du mit einem bekannten Winkel ganz einfach den anderen ausrechnen. Der Nebenwinkel ist quasi der Mathe-Helfer in der Not.
Kleiner Fun Fact: Wenn ein Winkel 90 Grad hat, ist sein Nebenwinkel… genau! Auch 90 Grad. Und das nennt man dann einen *rechten Winkel*. Hat wahrscheinlich irgendwann mal jemand festgelegt, weil er's grad so passend fand.
Wechselwinkel und Stufenwinkel – Die Linien-Tänzer
So, jetzt wird’s ein bisschen kniffliger, aber keine Angst, wir kriegen das hin! Stellt euch vor, es gibt zwei parallele Linien (die niemals streiten!) und eine dritte Linie, die beide schneidet (die sogenannte *Transversale*). Durch diese Konstellation entstehen ganz viele Winkel, und einige davon sind *Wechselwinkel* oder *Stufenwinkel*.
Die *Stufenwinkel* sind wie kleine Spione. Sie stehen an der gleichen "Stelle" an den beiden parallelen Linien. Stell dir vor, die parallelen Linien sind zwei Stockwerke eines Hauses. Die Stufenwinkel sind dann die Fenster, die in beiden Stockwerken an der gleichen Position sind. Und das Wichtigste: Sie sind gleich groß!
Und die *Wechselwinkel*? Die sind ein bisschen wie heimliche Liebhaber. Sie liegen auf unterschiedlichen Seiten der Transversalen und *zwischen* den parallelen Linien. Quasi auf der "Innenseite". Und ratet mal was? Auch die sind gleich groß!
Merkt euch einfach: Bei parallelen Linien und einer Transversalen sind Stufenwinkel und Wechselwinkel immer gleich groß. Das ist wie ein ungeschriebenes Gesetz der Geometrie. Wer dagegen verstößt, muss 100 Mal schreiben: "Parallele Linien sind meine Freunde!"
Warum das Ganze? – Der Sinn hinter dem Winkel-Wahnsinn
Okay, okay, ich hör euch schon: "Wozu brauche ich das alles überhaupt?" Gute Frage! Na ja, Winkel spielen in vielen Bereichen eine Rolle. Zum Beispiel in der Architektur (damit Häuser nicht umfallen), in der Navigation (damit Schiffe nicht im Kreis fahren) und in der Computergraphik (damit Videospiele nicht aussehen wie 'ne Pixel-Suppe). Und natürlich in der Mathematik selbst, weil… Mathematik halt.
Aber mal ehrlich, selbst wenn du nie wieder einen Winkel berechnen musst, ist es doch irgendwie cool, die kleinen Geheimnisse der Geometrie zu kennen, oder? Du kannst dann beim nächsten Spaziergang angeben und sagen: "Schau mal, da! Ein wunderschöner Scheitelwinkel! Und daneben ein perfekt geformter Nebenwinkel!" Deine Freunde werden begeistert sein (oder dich für verrückt erklären, aber das ist ja auch eine Art von Erfolg).
Und was das PDF betrifft? Na ja, da findest du alle Definitionen und Beweise nochmal ganz genau. Aber mal ehrlich, wer braucht schon ein PDF, wenn man so 'ne tolle Geschichte im Café gehört hat? 😉
Also, merkt euch die Winkel! Sie sind eure Freunde (oder zumindest eure Bekannten). Und jetzt geh ich mir noch 'nen Latte Macchiato bestellen. Prost!




