Welchen Flächeninhalt Hat Ein Gleichseitiges Dreieck Mit Dem Umfang 1m

Hallo, liebe Freunde der Geometrie! Habt ihr euch jemals gefragt, wie man eigentlich den Flächeninhalt eines gleichseitigen Dreiecks berechnet, wenn man nur den Umfang kennt? Ja, genau! Ein gleichseitiges Dreieck mit einem Umfang von einem Meter! Klingt erstmal kompliziert, oder? Aber keine Sorge, wir machen das zusammen und entdecken, wie viel Spaß Mathe eigentlich machen kann!

Warum überhaupt Flächeninhalt berechnen? Gute Frage! Stell dir vor, du bist Landschaftsgärtner und musst Rasen für ein dreieckiges Blumenbeet bestellen. Oder vielleicht bist du Architekt und planst ein futuristisches Gebäude mit dreieckigen Fenstern. In beiden Fällen (und in vielen anderen!) ist es super hilfreich, den Flächeninhalt berechnen zu können. Und mal ehrlich, wer will nicht mit beeindruckendem Mathe-Wissen glänzen?

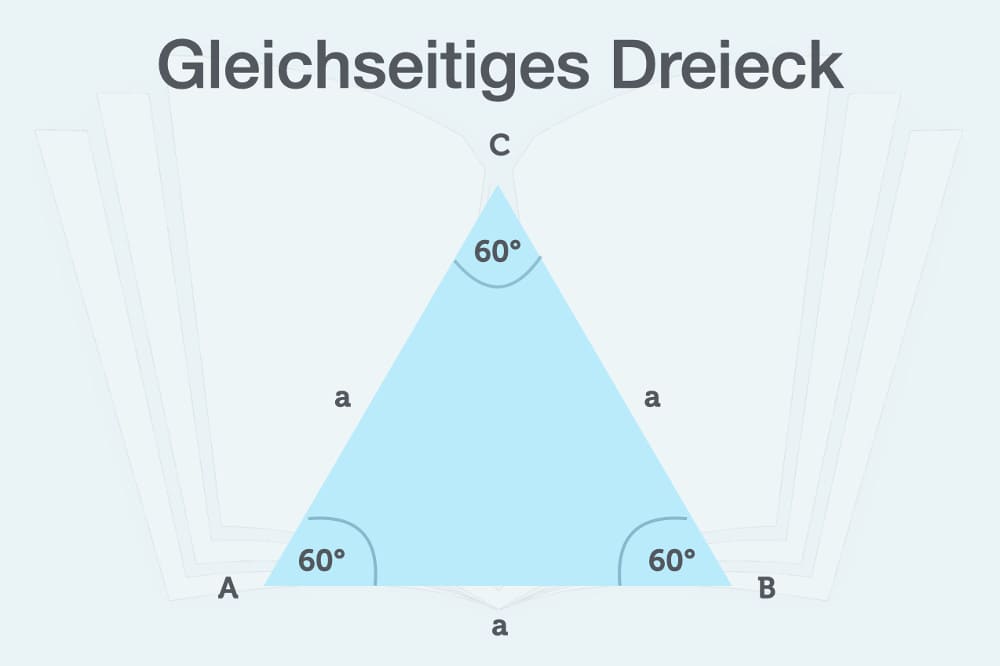
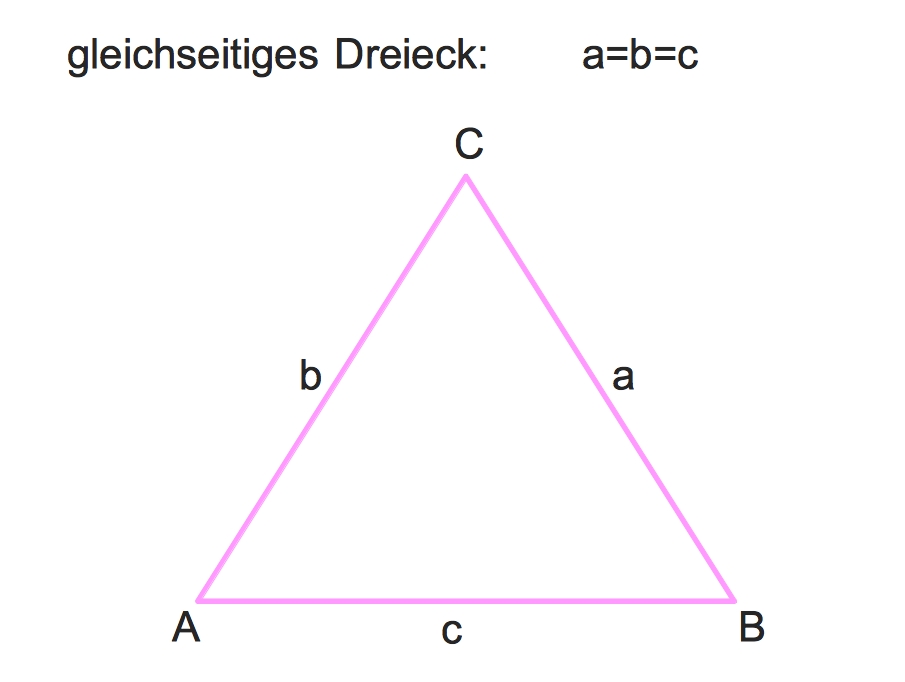
Also, lasst uns eintauchen! Was wissen wir? Wir wissen, dass unser Dreieck gleichseitig ist. Das bedeutet, alle drei Seiten sind gleich lang. Und wir wissen, dass der Umfang 1 Meter beträgt. Der Umfang ist die Summe aller Seiten, richtig? (Kleiner Reminder für alle, die's vergessen haben!).

Schritt 1: Seitenlänge berechnen

Da der Umfang 1 Meter ist und alle Seiten gleich lang sind, teilen wir den Umfang einfach durch 3! 1 Meter / 3 = 0,3333... Meter. Also ist jede Seite unseres gleichseitigen Dreiecks ungefähr 0,33 Meter lang. Oder, wenn wir es genauer haben wollen: 1/3 Meter! (Lasst uns der Einfachheit halber erstmal mit den Dezimalzahlen weiterrechnen, okay?).

Kurze Pause! Habt ihr bemerkt, wie wir aus einer einzigen Information – dem Umfang – bereits die Seitenlänge herausgefunden haben? Das ist doch schon mal ein Erfolg, oder? Mathe ist wie Detektivarbeit, nur mit Zahlen!

Schritt 2: Höhe berechnen

Jetzt kommt der etwas kniffligere Teil: die Höhe. Um den Flächeninhalt eines Dreiecks zu berechnen, brauchen wir die Grundseite (die kennen wir schon!) und die Höhe. Aber wie bekommen wir die Höhe? Keine Panik, hier kommt der Satz des Pythagoras ins Spiel! (Ja, der gute alte Pythagoras!).

Wir halbieren unser gleichseitiges Dreieck in zwei rechtwinklige Dreiecke. Die Grundseite des rechtwinkligen Dreiecks ist jetzt die Hälfte der ursprünglichen Seite (also 0,3333... Meter / 2 = 0,1666... Meter). Die Hypotenuse ist die ursprüngliche Seite (0,3333... Meter), und die Höhe ist die Seite, die wir suchen.

Der Satz des Pythagoras sagt: a² + b² = c², wobei a und b die Seiten des rechtwinkligen Dreiecks sind und c die Hypotenuse. In unserem Fall wollen wir b (die Höhe) herausfinden. Also formen wir die Formel um: b² = c² - a². Dann setzen wir ein: b² = (0,3333...)² - (0,1666...)².

Mit dem Taschenrechner (oder mit Kopfrechnen, wenn du ein Mathe-Genie bist!) bekommen wir: b² ≈ 0,0833. Um b (die Höhe) zu bekommen, ziehen wir die Quadratwurzel: b ≈ 0,2887 Meter. Also, die Höhe unseres gleichseitigen Dreiecks ist ungefähr 0,2887 Meter!

Schritt 3: Flächeninhalt berechnen

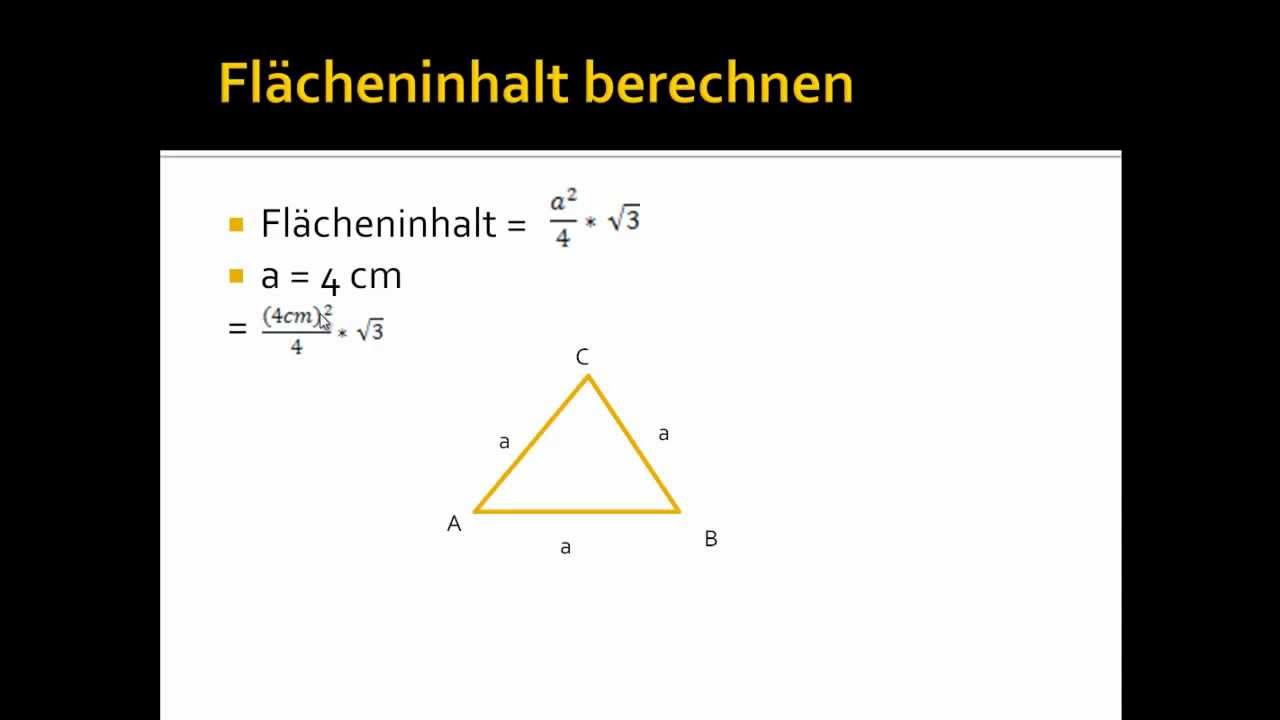
Endspurt! Jetzt, wo wir die Grundseite (0,3333... Meter) und die Höhe (0,2887 Meter) haben, können wir den Flächeninhalt berechnen. Die Formel für den Flächeninhalt eines Dreiecks ist: Flächeninhalt = (Grundseite * Höhe) / 2.

Also: Flächeninhalt = (0,3333... Meter * 0,2887 Meter) / 2 ≈ 0,0481 Quadratmeter.

Tada! Der Flächeninhalt unseres gleichseitigen Dreiecks mit einem Umfang von 1 Meter beträgt ungefähr 0,0481 Quadratmeter. Das ist weniger als eine halbe DIN A4 Seite!

Moment mal! Hätten wir die exakte Seitenlänge (1/3 Meter) verwendet, wäre die Berechnung etwas eleganter. Die exakte Höhe wäre (√3 / 6) Meter, und der exakte Flächeninhalt wäre (√3 / 36) Quadratmeter. Das ist zwar etwas schwieriger zu rechnen, aber mathematisch präziser!

Warum das Ganze?

Ich weiß, ich weiß, all diese Zahlen und Formeln können erstmal überwältigend sein. Aber sieh es mal so: Wir haben gerade bewiesen, dass wir ein kniffliges Geometrieproblem lösen können! Und das ist doch ein tolles Gefühl, oder? Mathe ist nicht nur etwas für Nerds, sondern ein mächtiges Werkzeug, um die Welt um uns herum zu verstehen und zu gestalten.

Und mal ehrlich, wer kann schon behaupten, den Flächeninhalt eines gleichseitigen Dreiecks mit einem Umfang von einem Meter im Schlaf aufsagen zu können? Du jetzt! (Fast jedenfalls… 😉)

Also, lass dich nicht entmutigen, wenn du mal eine Matheaufgabe nicht sofort verstehst. Bleib neugierig, probier herum, und scheue dich nicht, um Hilfe zu bitten. Die Welt der Mathematik ist voller spannender Entdeckungen, die nur darauf warten, von dir gemacht zu werden. Und wer weiß, vielleicht entdeckst du ja sogar deine Leidenschaft für Geometrie!

Also, ran an die Bücher (oder ans Internet!), und lass uns gemeinsam die Welt der Mathematik erobern!