Wie Berechnet Man Das Volumen Eines Parallelogramms
Hey du! Hast du dich jemals gefragt, wie man eigentlich das Volumen eines Parallelepipeds berechnet? Keine Panik, klingt komplizierter als es ist! Stell dir vor, du hast einen schiefen Quader vor dir stehen, so richtig schön lässig zur Seite gelehnt. Das ist im Grunde ein Parallelepiped. Und wir bringen ihm jetzt bei, seine Geheimnisse preiszugeben!
Was zum Teufel ist ein Parallelepiped überhaupt?
Ganz einfach: Ein Parallelepiped ist ein dreidimensionales Objekt, dessen sechs Seitenflächen alle Parallelogramme sind. Denk an einen verschobenen Schuhkarton, oder eine Ziegelsteinmauer, die ein bisschen getrunken hat. Hauptsache, alles ist irgendwie parallel, aber eben nicht unbedingt rechtwinklig. Das ist der ganze Trick! Und keine Sorge, wir brauchen keine komplizierten Formeln, um das Volumen zu berechnen. Es wird einfacher, versprochen!
Die Zutaten für unsere Volumen-Suppe
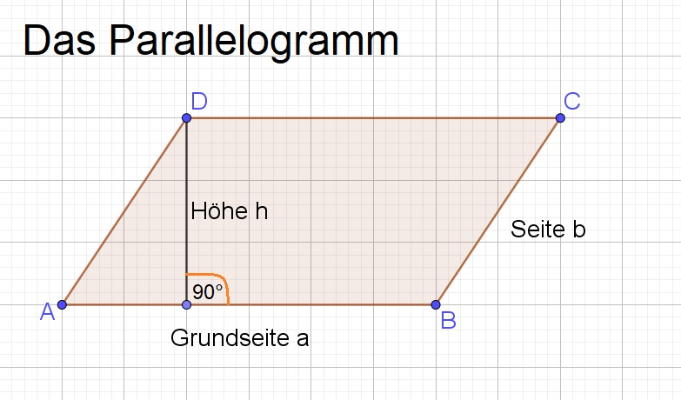
Um das Volumen unseres schiefen Freundes zu berechnen, brauchen wir drei magische Zutaten: Die Länge einer Seite (wir nennen sie einfach mal a), die Länge einer anderen Seite (nennen wir sie b), und die Höhe (h) des Parallelepipeds. Moment mal, Höhe? Ja, genau! Aber nicht die Höhe einer der Seitenflächen, sondern die senkrechte Höhe von der Grundfläche zur Deckfläche. Stell dir vor, du wirfst einen Dartpfeil senkrecht auf die Oberseite des Parallelepipeds – genau diese Strecke ist unsere Höhe!
Manchmal haben wir aber keine schnurgerade Höhe, sondern Winkel. Da wird's ein bisschen tricky, aber keine Sorge! Wenn du den Winkel (α) zwischen der Seite a und der Seite b kennst, und zusätzlich die Höhe h (die *nicht* senkrecht auf der Grundfläche steht), dann brauchst du eine winzige Prise Trigonometrie. Aber pssst, wir verraten es niemandem!
Das Rezept: So berechnen wir das Volumen!
Jetzt kommt der Clou! Das Volumen (V) eines Parallelepipeds berechnet sich mit folgender Formel, die einfacher ist als dein Lieblings-Spaghetti-Rezept:
V = a * b * h
Das war's schon! Länge mal Breite mal Höhe. Einfacher geht's kaum, oder? Stell dir vor, a ist 5 cm, b ist 4 cm und h ist 3 cm. Dann ist das Volumen: 5 cm * 4 cm * 3 cm = 60 cm³. Bingo!
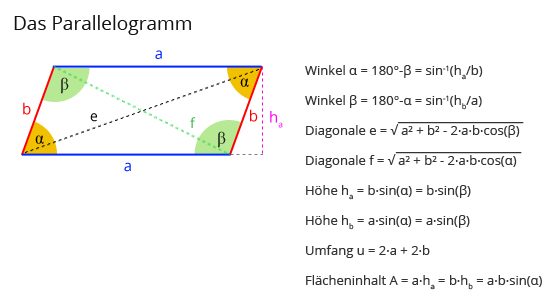
Und wenn wir den Winkel α im Spiel haben? Dann wird's ein klitzekleines bisschen komplizierter (aber wirklich nur ein bisschen!). Dann müssen wir die Höhe berechnen, die senkrecht auf der Grundfläche steht. Das geht mit:
h_senkrecht = h * sin(α)
Und dann setzen wir h_senkrecht in unsere erste Formel ein: V = a * b * h_senkrecht. Et voilà! Du hast es geschafft!
Beispiele, die das Leben schreibt (oder so ähnlich)
Stell dir vor, du baust ein Haus aus schiefen Lego-Steinen. Jeder Stein ist ein Parallelepiped. Um zu wissen, wie viele Steine du insgesamt brauchst, um dein gigantisches Lego-Schloss zu bauen, musst du das Volumen jedes Steins berechnen und dann alles addieren! (Okay, vielleicht übertreiben wir ein bisschen, aber das Prinzip stimmt!)
Oder: Du stapelst Bücher auf deinem Schreibtisch, aber nicht ordentlich, sondern so richtig schön chaotisch und schief. Wenn jedes Buch die Form eines Parallelepipeds hat, kannst du das Gesamtvolumen aller Bücher berechnen, um herauszufinden, wie viel Platz sie einnehmen. (Achtung: Könnte peinlich werden, wenn es zu viel ist!)
Fazit: Du bist ein Volumen-Meister!
Siehst du? Das Berechnen des Volumens eines Parallelepipeds ist gar keine Zauberei! Mit ein bisschen Wissen über Länge, Breite und Höhe (oder den Winkel) bist du bestens gerüstet, um jeden schiefen Quader zu bezwingen. Also, worauf wartest du noch? Schnapp dir ein Parallelepiped (oder irgendetwas, das zumindest so aussieht) und fang an zu rechnen! Du wirst sehen, es macht sogar Spaß! Und wenn nicht, dann hast du zumindest etwas gelernt, das du auf der nächsten Party zum Besten geben kannst. Wer weiß, vielleicht wirst du ja zum Star des Abends! Und denk dran: Albert Einstein hätte auch klein angefangen.