Wie Berechnet Man Den Betrag Eines Vektors
Okay, mal ehrlich, wer hat sich nicht schon mal gefragt, wie man den Betrag eines Vektors berechnet? Klingt erstmal nach totalem Nerd-Alarm, ich weiß. Aber glaub mir, das ist gar nicht so schlimm. Im Gegenteil, es ist sogar ziemlich nützlich, wenn man’s mal drauf hat. Stell dir vor, du bist beim Bäcker und willst wissen, wie weit du eigentlich von deinem Lieblings-Croissant entfernt bist. Oder, noch besser, du spielst Minigolf und musst abschätzen, wie hart du den Ball schlagen musst, um das blöde Loch endlich zu treffen. Da kommen Vektoren ins Spiel!
Was ist ein Vektor überhaupt? Na, im Grunde genommen ist das nur ein Pfeil. Ein Pfeil, der eine Richtung und eine Länge hat. Denk an eine Schatzkarte! "Gehe 5 Schritte nach Osten und 3 Schritte nach Norden." Das sind zwei Vektoren, die dich zum Schatz führen (oder zumindest zum Kühlschrank, wenn der Hunger groß ist).
Die Sache mit den Koordinaten
Jeder Vektor hat Koordinaten. Die sagen uns, wie weit der Pfeil in die jeweilige Richtung zeigt. Im zweidimensionalen Raum, also auf einem Blatt Papier oder deinem Minigolfplatz, haben wir meistens eine x-Koordinate (die horizontale Richtung) und eine y-Koordinate (die vertikale Richtung). Stell dir vor, der Croissant-Bäcker ist 4 Meter rechts und 3 Meter vor dir. Dann hat der Vektor, der dich zum Croissant führt, die Koordinaten (4, 3).
Und jetzt kommt der Clou: Der Betrag des Vektors ist einfach die Länge dieses Pfeils. Also, wie weit du wirklich zum Croissant laufen musst (Luftlinie, versteht sich. Wer läuft schon gern Umwege, wenn's ums Gebäck geht?).
Der Pythagoras lässt grüßen!
Wie berechnet man diese Länge? Hier kommt ein alter Bekannter ins Spiel: Pythagoras! Ja, genau, der Typ mit dem rechtwinkligen Dreieck. Erinnerst du dich noch an a² + b² = c²? Das brauchen wir jetzt!
Der Vektor mit seinen x- und y-Koordinaten bildet nämlich die Seiten eines rechtwinkligen Dreiecks. Der Betrag des Vektors ist dann die Hypotenuse, also die längste Seite.
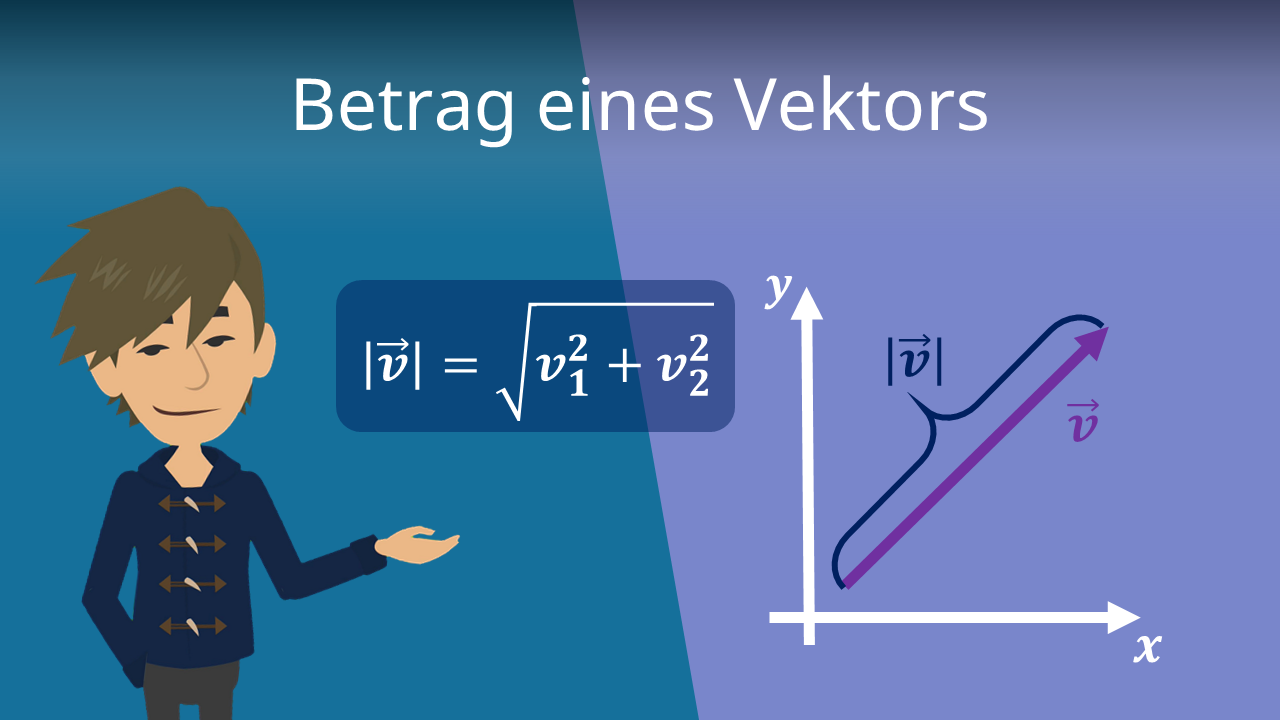
Die Formel: Der Betrag eines Vektors (x, y) ist √(x² + y²).
Beispiel: Unser Croissant-Vektor hat die Koordinaten (4, 3). Also ist der Betrag √(4² + 3²) = √(16 + 9) = √25 = 5. Du musst also 5 Meter laufen, um das Croissant zu bekommen. (Oder du lässt es dir liefern, ist ja auch eine Option.)
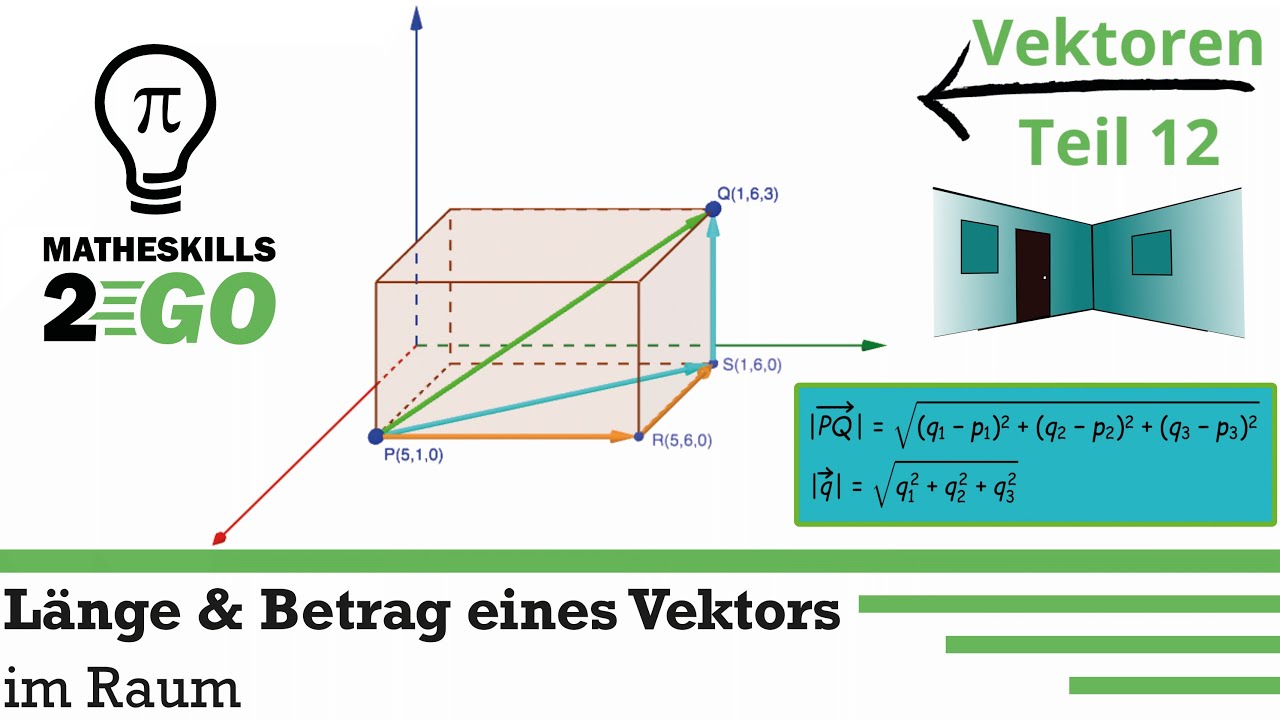
Und wenn es mehr als zwei Dimensionen sind?
Kein Problem! Das Prinzip bleibt gleich. Wenn du dich in einem dreidimensionalen Raum befindest (z.B. wenn du in einem riesigen Lager nach einer bestimmten Sorte Gummibärchen suchst), hast du auch eine z-Koordinate (die Höhe). Die Formel erweitert sich dann einfach zu: √(x² + y² + z²).
Stell dir vor, du suchst ein Gummibärchen, das 2 Meter nach rechts, 1 Meter nach vorne und 3 Meter nach oben liegt. Dann ist der Betrag des Vektors √(2² + 1² + 3²) = √(4 + 1 + 9) = √14. Du musst also ungefähr 3,74 Meter durch die Gummibärchen-Hölle krauchen, um dein Ziel zu erreichen.
Fazit: Kein Hexenwerk!
Siehst du? Den Betrag eines Vektors zu berechnen ist gar nicht so kompliziert. Es ist einfach nur Pythagoras in schick! Und wer weiß, vielleicht hilft dir das Wissen ja wirklich mal im Alltag. Sei es beim Bäcker, beim Minigolf oder bei der Gummibärchen-Suche. Hauptsache, du hast Spaß dabei!
Also, geh raus und miss die Welt! Und vergiss nicht, immer genug Croissants im Haus zu haben. 😉