Wie Berechnet Man Den Flächeninhalt Eines Gleichschenkligen Dreiecks

Okay, Leute, stellt euch vor: Ich sitze hier im Café, bestelle mir einen extra-großen Cappuccino (mit extra viel Milchschaum, versteht sich!), und grübele über... Flächen. Genauer gesagt, über die Fläche eines gleichschenkligen Dreiecks. Klingt erstmal nach Mathe-Folter, ich weiß. Aber keine Panik! Ich verspreche euch, das wird lustiger als der letzte Witz eures Onkels Gerd.

Was ist überhaupt ein gleichschenkliges Dreieck? Stell dir vor, du hast ein Dreieck, bei dem zwei Seiten gleich lang sind. Die dritte Seite, die so frech "unten" liegt, nennen wir dann die Basis. Und die beiden gleichen Seiten... na, die sind eben gleichschenklig. Fast wie bei einem symmetrischen Herz, nur halt mit Ecken. Denkt dran, Mathe ist Liebe!

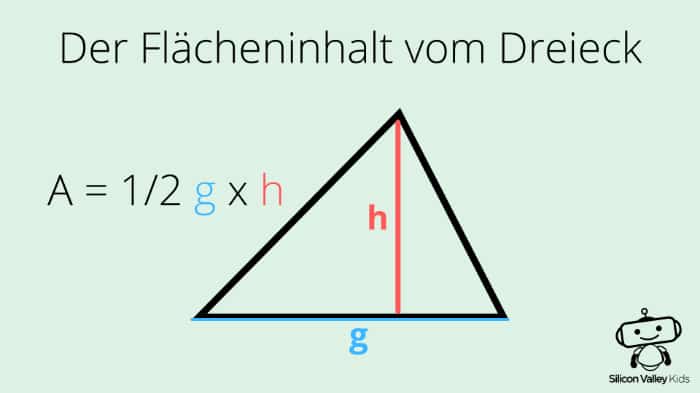
Die Standard-Methode: Basis mal Höhe, halbe-halbe!

Die klassische Methode, um die Fläche von *irgendeinem* Dreieck zu berechnen (und somit auch von einem gleichschenkligen), ist die altbekannte Formel: Fläche = (Basis * Höhe) / 2. Basis ist klar, das ist die untere Seite. Aber die Höhe? Die ist wie ein heimlicher Superheld, der senkrecht von der Spitze des Dreiecks (also dem Punkt, wo die beiden gleichlangen Seiten zusammentreffen) auf die Basis fällt.

Jetzt kommt der Clou: Bei einem gleichschenkligen Dreieck fällt diese Höhe genau in die Mitte der Basis! Tada! Das macht die Sache ein bisschen einfacher, finde ich. Wenn du also die Basis und die Höhe kennst, ist das Ganze ein Kinderspiel. Einfach einsetzen, ausrechnen, freuen! Du bist ein Mathe-Genie! Oder zumindest hast du ein Dreieck ausgerechnet. Auch gut!

Aber was, wenn uns die Höhe fehlt? Keine Panik, das ist, als wenn der Cappuccino ohne Milchschaum kommt. Eine Tragödie, aber lösbar!

Plan B: Pythagoras, mein alter Freund!

Wenn du nur die Länge der gleichlangen Seiten (nennen wir sie mal 's') und die Länge der Basis (nennen wir sie 'b') kennst, dann kommt Pythagoras ins Spiel. Ja, der Typ mit dem rechtwinkligen Dreieck. Erinnert ihr euch an den guten alten Pythagoras: a² + b² = c²?

Wir können uns nämlich vorstellen, dass die Höhe unser gleichschenkliges Dreieck in zwei *rechtwinklige* Dreiecke teilt. Die Basis jedes dieser kleinen Dreiecke ist dann b/2 (die Hälfte der Basis des großen Dreiecks). Die lange Seite des rechtwinkligen Dreiecks ist 's' (eine der gleichlangen Seiten des gleichschenkligen Dreiecks). Und die Höhe ist… genau! Die Seite, die wir suchen!

Also: Höhe² = s² - (b/2)². Um die Höhe zu bekommen, musst du dann noch die Wurzel aus dem Ergebnis ziehen.

Uff! Kurz durchatmen. Klingt kompliziert, ist es aber gar nicht. Stell dir vor, du baust mit Lego. Du zerlegst das große Dreieck in kleinere Teile, rechnest was aus, und setzt es wieder zusammen. Und am Ende hast du die Höhe. Super! Jetzt kannst du die Flächenformel von oben benutzen: Fläche = (Basis * Höhe) / 2.

Wichtiger Hinweis: Verwechselt die Seiten nicht! Das ist wie Kaffee mit Salz statt Zucker: ungenießbar!

Heron's Formel: Für die ganz Faulen (oder sehr Schlauen)!

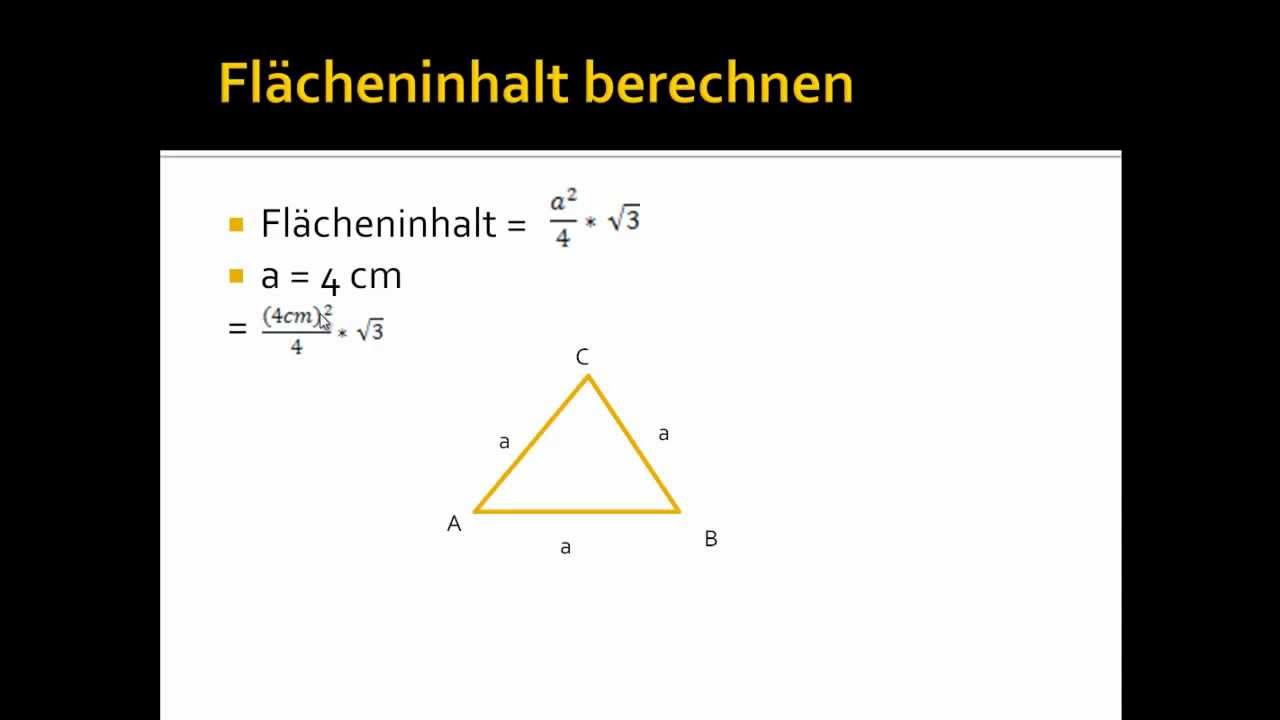
Es gibt noch eine dritte Möglichkeit, die Fläche eines Dreiecks zu berechnen, die nennt sich Heron's Formel. Die ist besonders nützlich, wenn du alle drei Seiten kennst. Im Falle eines gleichschenkligen Dreiecks kennst du ja zwei davon (die beiden gleichlangen Seiten) und die Basis.

Heron's Formel ist ein bisschen komplizierter, aber keine Angst, ich erkläre sie ganz langsam. Zuerst berechnen wir den "halben Umfang" (s), das ist die Summe aller drei Seiten geteilt durch zwei: s = (a + b + c) / 2. Da wir ein gleichschenkliges Dreieck haben, ist a = c = s (gleich lange Seite). Also s = (s + s + b) / 2 oder s = (2s + b) / 2.

Dann kommt der magische Moment: Fläche = √[s * (s - a) * (s - b) * (s - c)]. Oder in unserem Fall: Fläche = √[s * (s - s) * (s - b) * (s - s)]. Moment mal… (s-s) ist ja Null! Das vereinfacht die Sache enorm! Nein, Moment, stopp! Das war ein Denkfehler! Wir müssen die allgemeine Formel nutzen!

Die korrekte Formel mit den Seiten a, a und b sieht dann so aus: Fläche = √[s * (s - a) * (s - a) * (s - b)]. Ja, das ist etwas Arbeit, aber hey, du hast die Wahl!

Fazit: Dreiecke sind cool! (Und berechenbar!)

So, da haben wir es! Drei verschiedene Wege, um die Fläche eines gleichschenkligen Dreiecks zu berechnen. Ob du nun der Typ für die klassische Methode bist, der Pythagoras-Jünger oder der Heron-Fan, ist ganz dir überlassen. Hauptsache, du kommst zum richtigen Ergebnis. Und wenn nicht, dann bestell dir einfach noch einen Cappuccino und versuch es nochmal.

Denn eins ist sicher: Mit ein bisschen Übung (und vielleicht einem guten Mathe-Buch) ist die Berechnung der Fläche eines gleichschenkligen Dreiecks kein Hexenwerk. Und wer weiß, vielleicht beeindruckst du ja beim nächsten Kaffeeklatsch deine Freunde mit deinem neu erworbenen Wissen. "Wisst ihr eigentlich, wie man die Fläche eines gleichschenkligen Dreiecks berechnet...?" Der Held des Abends bist du!

So, und jetzt gönne ich mir erstmal meinen Cappuccino. Prost!