Wie Berechnet Man Den Satz Des Pythagoras

Ich erinnere mich noch genau an meine Schulzeit, als unser Mathelehrer Herr Schmidt uns mit dem Satz des Pythagoras quälte. Er hatte diese unglaubliche Fähigkeit, selbst die simpelsten Dinge kompliziert klingen zu lassen. "A Quadrat plus B Quadrat gleich C Quadrat!" hallte es durch den Raum. Ich dachte nur: "Warum, Herr Schmidt, warum? Wann brauche ich das im echten Leben?" Tja, kleine Ahnung hatte ich, dass dieser "C Quadrat"-Mist mir später noch oft begegnen würde – und dass er gar nicht so kompliziert ist, wie Herr Schmidt ihn darstellte.
Also, lasst uns das Ding mal entmystifizieren, ja? Der Satz des Pythagoras ist eigentlich super easy, versprochen! Er beschreibt eine Beziehung zwischen den Seiten eines rechtwinkligen Dreiecks. Und nur die, merken wir uns das.
Was ist ein rechtwinkliges Dreieck? Ganz einfach: Ein Dreieck, das einen 90-Grad-Winkel hat (so ein Winkel sieht aus wie eine Ecke). Die Seite, die gegenüber vom rechten Winkel liegt, ist die längste Seite im Dreieck und wird Hypotenuse genannt (das ist das "C" im Pythagoras-Satz). Die beiden anderen Seiten, die den rechten Winkel bilden, nennt man Katheten (das sind "A" und "B").
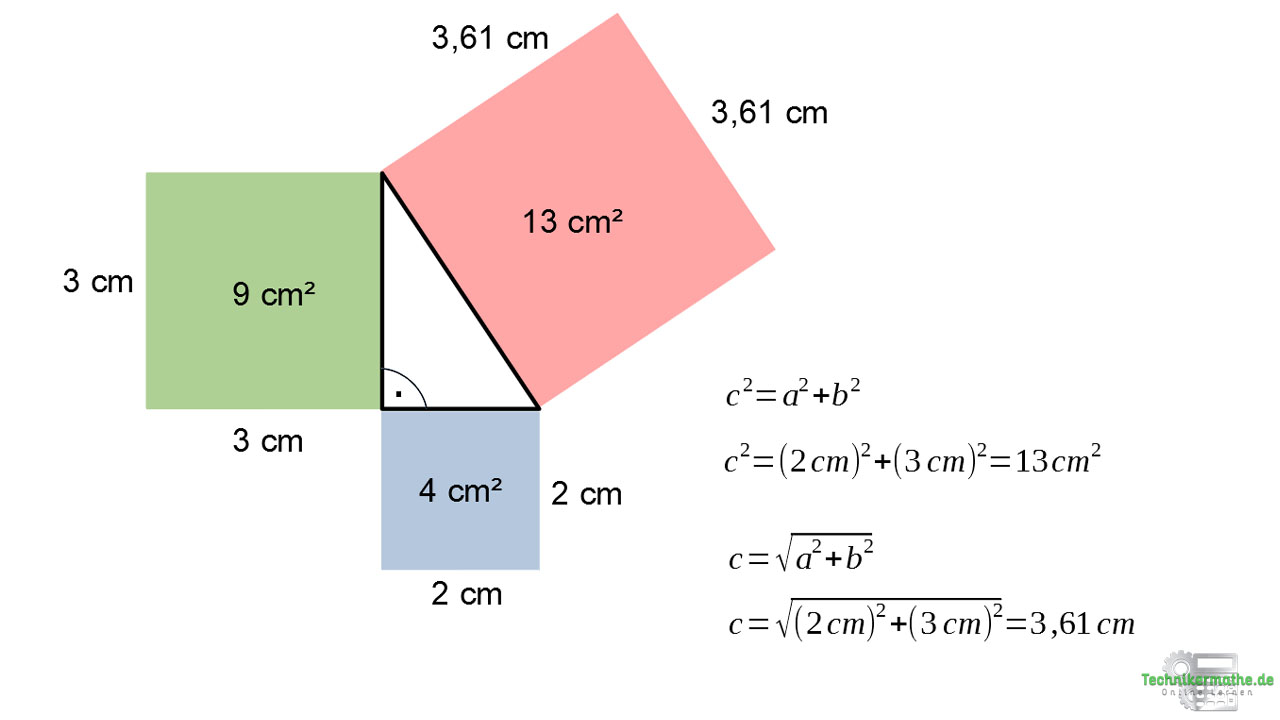
Und jetzt kommt der Clou: Der Satz des Pythagoras besagt, dass die Summe der Quadrate der Katheten gleich dem Quadrat der Hypotenuse ist. Klingt kompliziert? Ist es aber nicht! In Formel-Schreibweise sieht das so aus:
a² + b² = c²
"Quadrat" bedeutet einfach, dass man eine Zahl mit sich selbst multipliziert. Also a² ist a mal a. Simpel, oder?
Wie berechnet man das jetzt?
Stellen wir uns vor, wir haben ein rechtwinkliges Dreieck. Eine Kathete (a) ist 3 cm lang, die andere (b) ist 4 cm lang. Wir wollen herausfinden, wie lang die Hypotenuse (c) ist.
So geht's:
- Setze die Werte in die Formel ein: 3² + 4² = c²
- Berechne die Quadrate: 9 + 16 = c²
- Addiere die Ergebnisse: 25 = c²
- Jetzt kommt der Trick: Um c herauszufinden, müssen wir die Wurzel aus 25 ziehen. Die Wurzel aus 25 ist 5 (weil 5 mal 5 gleich 25 ist).
Also ist die Hypotenuse (c) 5 cm lang. Voila!
Achtung: Die Wurzel zu ziehen ist der Knackpunkt! Dafür brauchst du entweder einen Taschenrechner (die meisten Smartphones haben einen) oder du kennst die gängigen Quadratzahlen auswendig. (Kleiner Tipp: 1²=1, 2²=4, 3²=9, 4²=16, 5²=25, 6²=36, 7²=49, 8²=64, 9²=81, 10²=100 – das hilft schonmal!)
Was, wenn wir die Hypotenuse und eine Kathete kennen und die andere Kathete berechnen wollen? Kein Problem! Wir stellen die Formel einfach um.
Angenommen, wir kennen c (die Hypotenuse) und a (eine Kathete) und wollen b (die andere Kathete) herausfinden. Dann stellen wir die Formel a² + b² = c² um zu:
b² = c² - a²
Und dann gehen wir genauso vor wie vorher: Werte einsetzen, Quadrate berechnen, subtrahieren und am Ende die Wurzel ziehen.
Wo brauch ich das im echten Leben?
Überraschend oft! Beim Bauen, beim Navigieren (denk an GPS!), in der Computergrafik... Überall, wo es um Dreiecke und Abstände geht. Vielleicht willst du ja auch nur wissen, ob dein neuer Fernseher in die Ecke passt. Der Satz des Pythagoras hilft dir dabei!
Also, keine Angst vor Herrn Schmidt und seinem "C Quadrat"! Mit ein bisschen Übung ist der Satz des Pythagoras kinderleicht. Und wer weiß, vielleicht beeindruckst du ja bald deine Freunde mit deinem neuen Wissen über rechtwinklige Dreiecke! (Oder du berechnest, ob die Pizza wirklich rund ist. Man weiß ja nie...)