Wie Berechnet Man Den Umfang Eines Parallelogramms Aus

Hey du! Stell dir vor, du sitzt gemütlich im Café, trinkst deinen Latte Macchiato und plötzlich... BAM! Die Frage aller Fragen taucht auf: "Wie berechnet man eigentlich den Umfang eines Parallelogramms?" Keine Panik! Ich bin hier, um dir zu helfen. Und versprochen, es wird einfacher, als einen doppelten Espresso zu bestellen!
Zuerst mal: Was ist überhaupt ein Parallelogramm? Stell dir ein Rechteck vor, das jemand leicht schief angestoßen hat. Zack! Fertig ist das Parallelogramm. Es hat zwei Paare von parallelen Seiten, wobei die gegenüberliegenden Seiten gleich lang sind. So weit, so gut, oder?
Die einfache Formel: So geht's kinderleicht!
Okay, jetzt kommt der Clou. Der Umfang eines Parallelogramms ist nichts anderes als die Summe aller seiner Seiten. Klingt kompliziert? Ist es aber nicht! Stell dir vor, du gehst einmal komplett um das Parallelogramm herum. Die Strecke, die du zurücklegst, ist der Umfang.
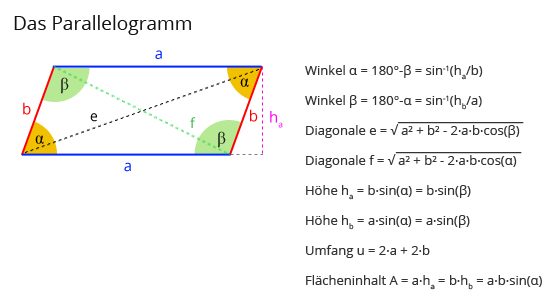
Die Formel lautet also: U = 2a + 2b
"U" steht für Umfang (Überraschung!), "a" ist die Länge einer Seite und "b" die Länge der anderen Seite. Denk dran, die gegenüberliegenden Seiten sind ja gleich lang, deshalb müssen wir jede Seite nur zweimal berücksichtigen.
Ein kleines Beispiel, um das Ganze zu veranschaulichen:
Sagen wir mal, eine Seite (a) ist 5 cm lang und die andere Seite (b) ist 3 cm lang. Dann rechnest du:
U = 2 * 5 cm + 2 * 3 cm
U = 10 cm + 6 cm
U = 16 cm
Tataa! Der Umfang des Parallelogramms beträgt 16 cm. War doch gar nicht so schlimm, oder?
Kleine Stolpersteine und wie du sie umgehst
Klar, manchmal gibt es kleine Fallen, in die man tappen kann. Zum Beispiel, wenn die Längen der Seiten in unterschiedlichen Einheiten angegeben sind (Meter und Zentimeter zum Beispiel). Dann musst du sie zuerst in dieselbe Einheit umrechnen, bevor du losrechnest. Sonst kommt Murks raus! Stell dir vor, du addierst Äpfel mit Birnen... das schmeckt auch nicht!
Oder was ist, wenn du nur eine Seite und einen Winkel gegeben hast? Keine Sorge, da gibt es dann andere mathematische Tricks, die ins Spiel kommen (Sinus, Kosinus und Co.), aber das ist Stoff für einen anderen Latte Macchiato-Plausch. Für den Umfang brauchst du wirklich nur die Längen der beiden unterschiedlichen Seiten.
Warum ist das überhaupt wichtig?
Gute Frage! Vielleicht denkst du jetzt: "Wann brauche ich das im echten Leben?" Nun ja, vielleicht musst du einen Bilderrahmen bauen, der die Form eines Parallelogramms hat. Oder du möchtest deinen Garten mit einem Beet in Parallelogramm-Form verschönern und brauchst die richtige Länge für den Zaun. Man weiß ja nie! Und hey, Mathe ist auch super fürs Gehirn, hält dich fit!
Bonus-Tipp: Wenn du dir mal unsicher bist, zeichne dir das Parallelogramm auf! Visualisierung hilft ungemein. Und es macht Spaß, ein bisschen zu kritzeln. Hauptsache, du verwechselst es nicht mit einem Drachenviereck, das ist nämlich was ganz anderes!
Also, mein Freund, jetzt bist du ein echter Parallelogramm-Umfangs-Experte! Du kannst ab sofort mit deinem Wissen glänzen und jeden beeindrucken. Und wenn dich jemand fragt, wie man das berechnet, sag einfach: "Kein Problem, ich hab's drauf!" Und dann zwinkerst du ihm verschmitzt zu.
Denk daran: Mathe muss nicht trocken und langweilig sein. Mit ein bisschen Humor und der richtigen Erklärung kann es sogar richtig Spaß machen. Und hey, wenn du das hier verstanden hast, bist du bereit für die nächste mathematische Herausforderung! Also, Kopf hoch, Brust raus und ran an die Aufgaben! Du schaffst das!