Wie Berechnet Man Die Höhe Eines Trapez

Also, hört mal zu, Leute! Ich hab' da 'ne Story, die beginnt mit 'nem Trapez. Ja, genau, diese komische Form, die aussieht wie ein Haus, das jemandem auf's Dach gestiegen ist. Aber keine Sorge, wir werden das Ding vermessen! Wir reden hier vom Berechnen der Höhe. Klingt kompliziert? Papperlapapp! Ist einfacher als Spaghetti kochen - versprochen!

Ich saß neulich im Café, versuche mir vorzustellen, wie ein Trapez wohl schmecken würde (vielleicht ein bisschen nach abgestandenem Linoleum?), als mein Kumpel Klaus ankam. Klaus, der Mathe-Magier. Der Typ kann im Kopf Quadratwurzeln ziehen, während ich noch versuche, die richtige Kaffee-Sorte auszusprechen. Er grinst mich an und sagt: "Na, mal wieder am Rätseln? Diesmal 'n Trapez, was?"

Tja, und da waren wir. Mitten in der Diskussion, wie man dieses verdammte Ding vermisst. "Die Höhe, mein Freund, die Höhe! Das ist der springende Punkt!", rief Klaus, so laut, dass die Barista uns komisch ansah. Aber hey, Mathe ist nun mal aufregend, oder?

Was wir wirklich wissen müssen

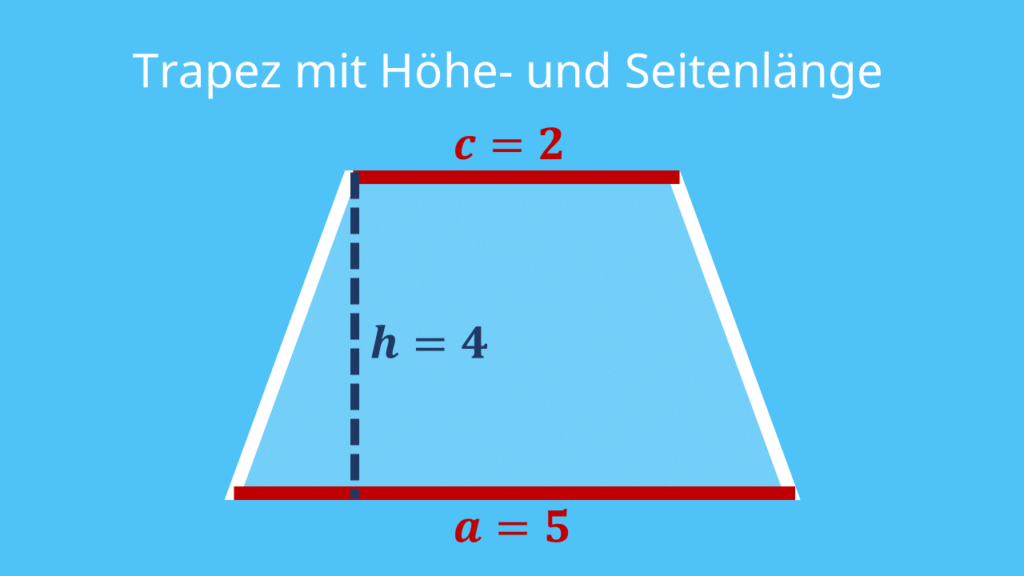
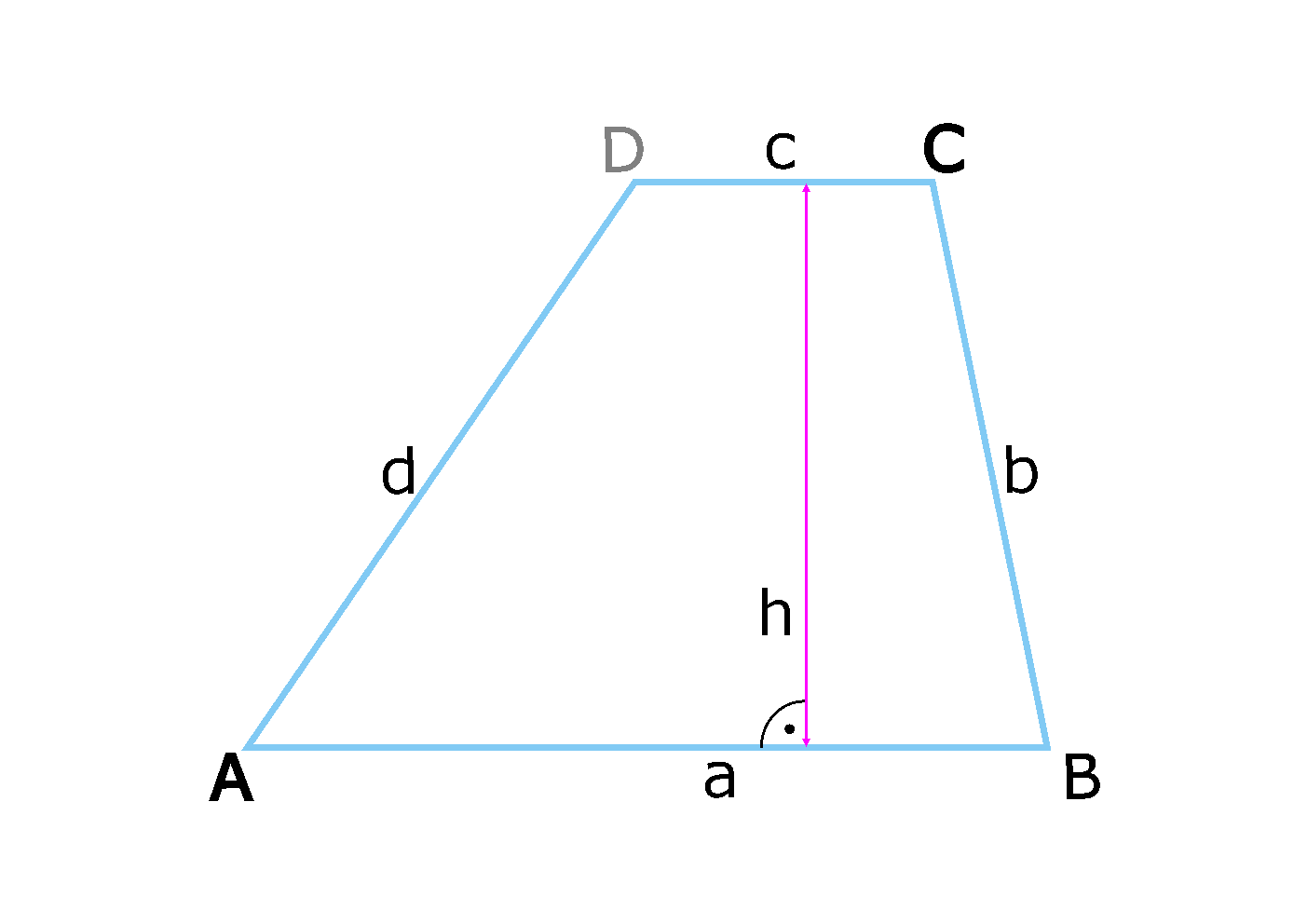
Okay, bevor wir uns in Formeln verstricken, erstmal das Wesentliche. Ein Trapez hat zwei parallele Seiten (die nennen wir mal a und c – total kreativ, ich weiß!) und zwei nicht-parallele Seiten (die ignorieren wir erstmal gekonnt). Die Höhe (h) ist der senkrechte Abstand zwischen den parallelen Seiten. Stellt euch vor, es ist die Leiter, die ihr braucht, um vom unteren Stockwerk (Seite a) zum oberen Stockwerk (Seite c) zu gelangen.

So, und jetzt kommt der Trick: Wir brauchen mehr Infos! Entweder wir kennen den Flächeninhalt (A) des Trapezes, oder wir haben Glück und kennen andere nützliche Dinge, wie zum Beispiel die Längen der Seiten und den Winkel zwischen den Seiten. Falls nicht, müssen wir uns auf die Jagd nach diesen Infos machen! Stellt euch vor, ihr seid Indiana Jones, aber statt 'ner Peitsche habt ihr 'nen Taschenrechner.

Option 1: Wir kennen den Flächeninhalt

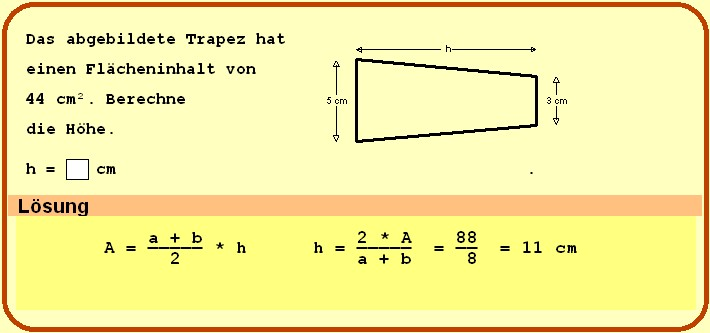
Das ist der Jackpot! Wenn ihr den Flächeninhalt kennt, wird's richtig easy. Die Formel, die uns rettet, lautet:

A = (a + c) / 2 * h

Wo A der Flächeninhalt ist, a und c die Längen der parallelen Seiten sind, und h – unser gesuchtes Opfer – die Höhe ist. Um h zu finden, stellen wir die Formel einfach um:

h = 2 * A / (a + c)

Bäm! Fertig! Einfach den Flächeninhalt verdoppeln, durch die Summe der parallelen Seiten teilen, und ihr habt die Höhe. So einfach, dass sogar Klaus' Katze das verstehen würde (vielleicht!).

Option 2: Keine Panik, wir improvisieren!

Okay, was, wenn wir den Flächeninhalt nicht kennen? Nicht verzagen, Klaus fragen! Er hat mir nämlich noch 'nen Trick verraten. Manchmal kennen wir andere nützliche Informationen, die uns helfen können. Zum Beispiel, wenn wir das Trapez in ein Rechteck und zwei rechtwinklige Dreiecke zerlegen können. Oder...nun ja, es gibt viele Möglichkeiten, und jede ist ein eigenes kleines Mathe-Abenteuer.

Nehmen wir mal an, wir kennen die Längen der nicht-parallelen Seiten (b und d) und den Winkel zwischen einer dieser Seiten und der längeren parallelen Seite (z.B. Winkel α zwischen Seite b und Seite a). Dann können wir mit Trigonometrie zaubern! (Keine Sorge, ist nicht so schlimm, wie es klingt.)

Wir brauchen den Sinus des Winkels α (sin(α)). Und dann gilt:

h = b * sin(α)

Tada! Die Höhe ist die Länge der Seite b multipliziert mit dem Sinus des Winkels α. Ist das nicht magisch? Fast so magisch wie ein gut gezapftes Bier nach 'ner langen Mathe-Session!

Warum das Ganze?

Jetzt fragt ihr euch vielleicht: "Warum zur Hölle sollte ich die Höhe eines Trapezes berechnen wollen?". Gute Frage! Vielleicht wollt ihr ein Trapez-förmiges Blumenbeet anlegen. Oder ein Raumschiff bauen, das die Form eines Trapezes hat. Oder einfach nur eure Freunde im Café mit eurem unglaublichen Mathe-Wissen beeindrucken. Die Möglichkeiten sind endlos! Und mal ehrlich, wer will nicht mit Trapez-Kenntnissen glänzen?

Also, Leute, merkt euch: Keine Angst vor Trapezen! Mit ein bisschen Wissen, 'ner Prise Humor und vielleicht 'ner Tasse Kaffee (oder zwei) könnt ihr jede Höhe meistern. Und wenn ihr mal wieder nicht weiterwisst, fragt einfach Klaus. Oder mich. Wir helfen gerne! Denn Mathe kann auch Spaß machen – vor allem, wenn man's mit Humor nimmt!