Wie Berechnet Man Die Kantenlänge Eines Würfels

Na, schon mal über Würfel nachgedacht? Klar, kennst du. Aber hast du dich jemals gefragt, wie man die Kantenlänge so eines perfekten, geometrischen Freundes ausrechnet? Keine Sorge, das ist kein Hexenwerk! Stell dir vor, wir sind auf Schatzsuche, und die Schatzkarte führt uns direkt zur Lösung.
Warum ist das überhaupt wichtig? Okay, vielleicht planst du gerade kein ultra-geheimes Würfel-Imperium. Aber das Wissen, wie man so etwas ausrechnet, ist total nützlich. Ob du nun ein Regal baust, ein Kuchenrezept umrechnest oder einfach nur deinen Freunden mit deinem mathematischen Scharfsinn imponieren willst: Los geht's!
Der Schlüssel zur Kiste: Das Volumen
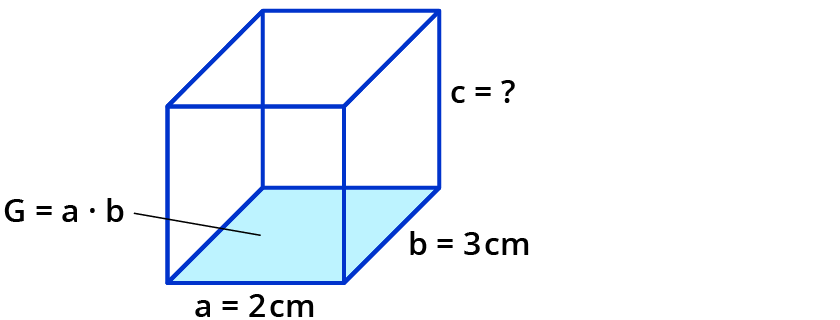
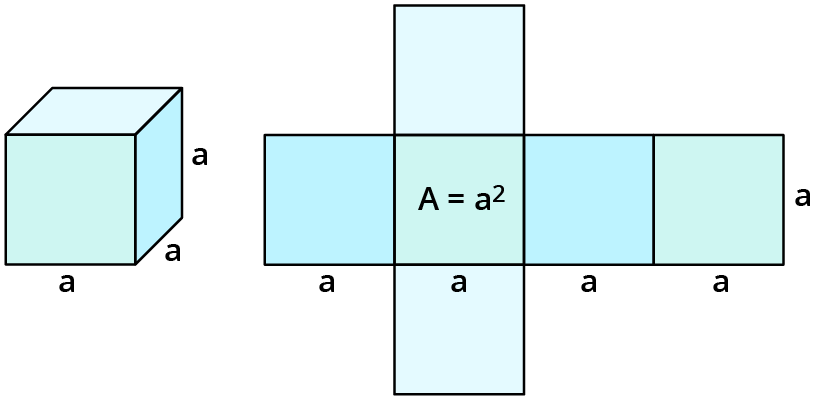
Das Wichtigste zuerst: Das Volumen. Stell dir vor, du füllst den Würfel mit Wasser. Die Menge an Wasser, die reinpasst, ist sein Volumen. Haben wir das Volumen gegeben, wird es interessant!
Also, was ist die Formel? Ganz einfach: Volumen = Kantenlänge * Kantenlänge * Kantenlänge. Kurz gesagt: V = a³. Das "a" steht für die Kantenlänge. Und dieses kleine Dreierlein da oben bedeutet: "multipliziere 'a' mit sich selbst, und das Ergebnis nochmal mit 'a'."
Mathematik kann so poetisch sein, oder?
Die Zauberformel: Die Kubikwurzel
Okay, jetzt kommt der Clou. Wir wollen ja "a" wissen, die Kantenlänge. Also müssen wir die Formel umstellen. Und das führt uns zur Kubikwurzel.
Keine Panik! Denk an die Kubikwurzel als den Gegenspieler des "hoch drei". Sie macht die Multiplikation wieder rückgängig. Die Formel sieht dann so aus: Kantenlänge (a) = Kubikwurzel aus dem Volumen (V).
Stell dir vor, die Kubikwurzel ist wie ein Zauberspruch, der das Volumen des Würfels in seine ursprüngliche Kantenlänge zurückverwandelt. Abrakadabra! Und schon hast du die Lösung.
Kleiner Fun Fact: Die Kubikwurzel ist das Gegenteil der Potenzierung mit 3. So wie Addition das Gegenteil von Subtraktion ist.
Ein Beispiel gefällig?
Sagen wir, unser Würfel hat ein Volumen von 64 Kubikzentimetern. Das heißt, V = 64 cm³. Was ist also die Kantenlänge?
Wir brauchen die Kubikwurzel aus 64. Und die ist... 4! Warum? Weil 4 * 4 * 4 = 64. Die Kantenlänge beträgt also 4 Zentimeter. Tadaa!
Und wenn du keinen Taschenrechner zur Hand hast? Viele Taschenrechner haben eine Kubikwurzel-Taste. Ansonsten helfen dir Online-Rechner weiter. Oder du fragst einfach einen Mathe-Nerd. Die freuen sich immer über solche Fragen.
Wo ist der Haken? (Spoiler: Gibt keinen)
Ehrlich gesagt? Es gibt keinen großen Haken. Die Schwierigkeit liegt oft eher darin, das Volumen des Würfels herauszufinden. Aber wenn du das hast, ist der Rest ein Kinderspiel.
Manchmal ist das Volumen vielleicht nicht direkt gegeben. Vielleicht musst du es erst aus anderen Informationen ableiten. Aber das ist dann schon die nächste Stufe der Schatzsuche!
Denk dran: Übung macht den Meister!
Mehr als nur Mathematik
Das Ausrechnen der Kantenlänge eines Würfels mag auf den ersten Blick trocken erscheinen. Aber es ist ein Beispiel dafür, wie Mathematik die Welt um uns herum beschreibt. Es geht um Zusammenhänge, um das Verstehen von Formen und Räumen. Und darum, dass auch vermeintlich einfache Dinge eine faszinierende innere Struktur haben.
Also, das nächste Mal, wenn du einen Würfel siehst, denk daran: Da steckt mehr dahinter, als man auf den ersten Blick sieht. Und jetzt weißt du auch, wie du seine Geheimnisse lüften kannst! Viel Spaß beim Knobeln!
Und noch ein Fun Fact: Wusstest du, dass es Würfel gibt, die gar keine perfekten Würfel sind? Denk mal an Spielwürfel, bei denen die "6" etwas schwerer ist, damit sie öfter gewürfelt wird. (Psst, nicht weitersagen!).