Wie Berechnet Man Nullstellen Bei Parabeln Aus

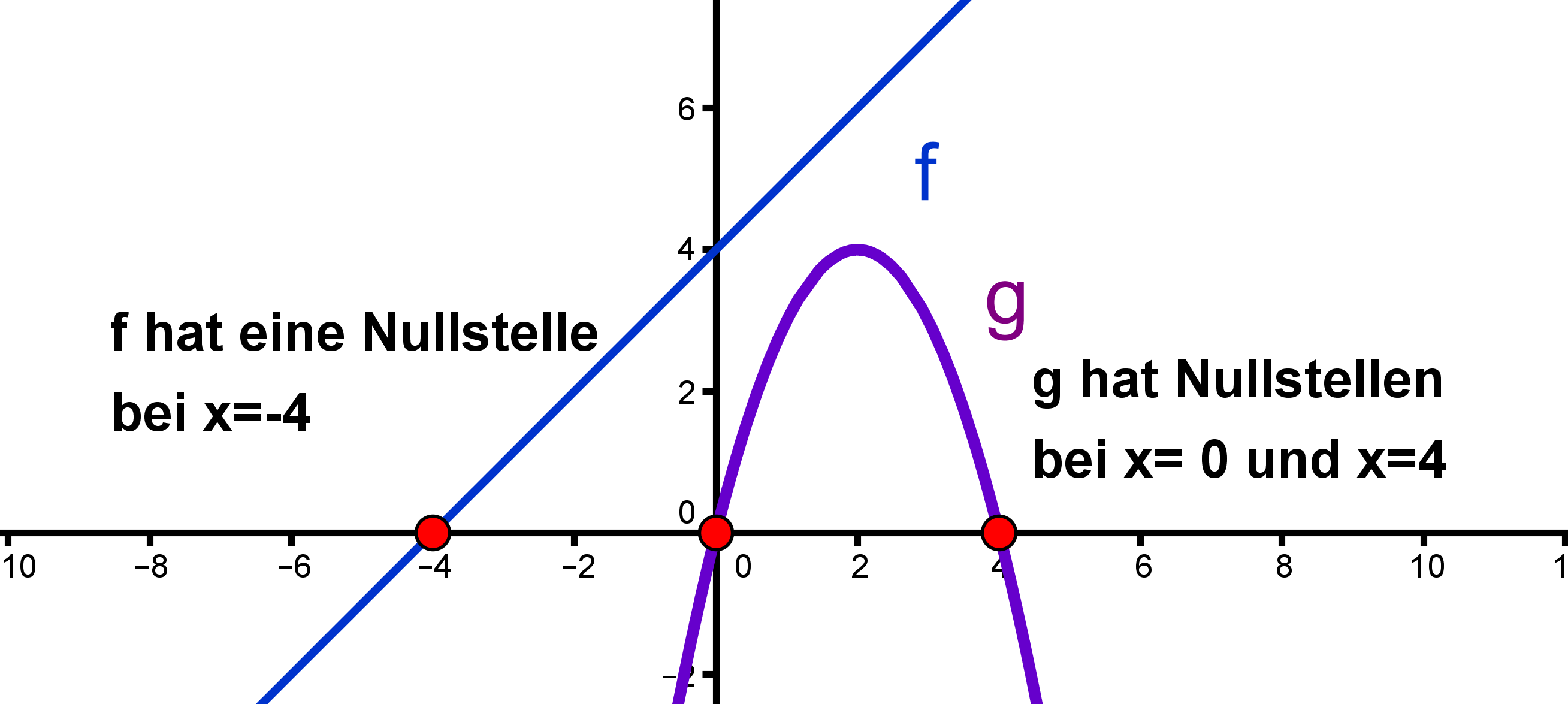
Parabeln, diese elegant geschwungenen Linien, begegnen uns überall: in der Architektur von Brücken, im Flug von Bällen und sogar in der Form von Satellitenschüsseln. Doch weit mehr als nur ein mathematisches Konzept, sind Parabeln ein Schlüssel zu kreativen Ausdrucksformen und faszinierenden Problemlösungen. Und das Berechnen ihrer Nullstellen, also der Punkte, an denen sie die x-Achse kreuzen, ist einfacher als du denkst!
Warum sollte das nun für Künstler, Hobbybastler oder einfach nur neugierige Geister interessant sein? Ganz einfach: Das Verständnis von Parabeln eröffnet neue Perspektiven. Für Künstler können Nullstellen helfen, präzise Kurven in Skulpturen oder Gemälden zu konstruieren. Hobbybastler können sie nutzen, um beispielsweise Solaröfen zu optimieren oder die Bahn von Modellraketen zu berechnen. Und für alle anderen ist es ein schönes Beispiel dafür, wie Mathematik die Welt um uns herum erklärt und uns hilft, sie besser zu verstehen.
Stell dir vor, du gestaltest eine moderne Skulptur, bei der eine Parabel eine zentrale Rolle spielt. Durch das Berechnen der Nullstellen kannst du exakt bestimmen, wo die Basis der Parabel auf dem Boden aufliegt. Oder du entwirfst einen minimalistischen Couchtisch, dessen Beine in Form von Parabeln gestaltet sind. Die Nullstellen geben dir die genauen Maße für die Auflagefläche. Aber auch in weniger konkreten Bereichen, wie beim Programmieren von Spielen, sind Parabeln nützlich, um beispielsweise die Flugbahn von Projektilen realistisch darzustellen. Die Nullstellen helfen dabei, das Ziel zu definieren.
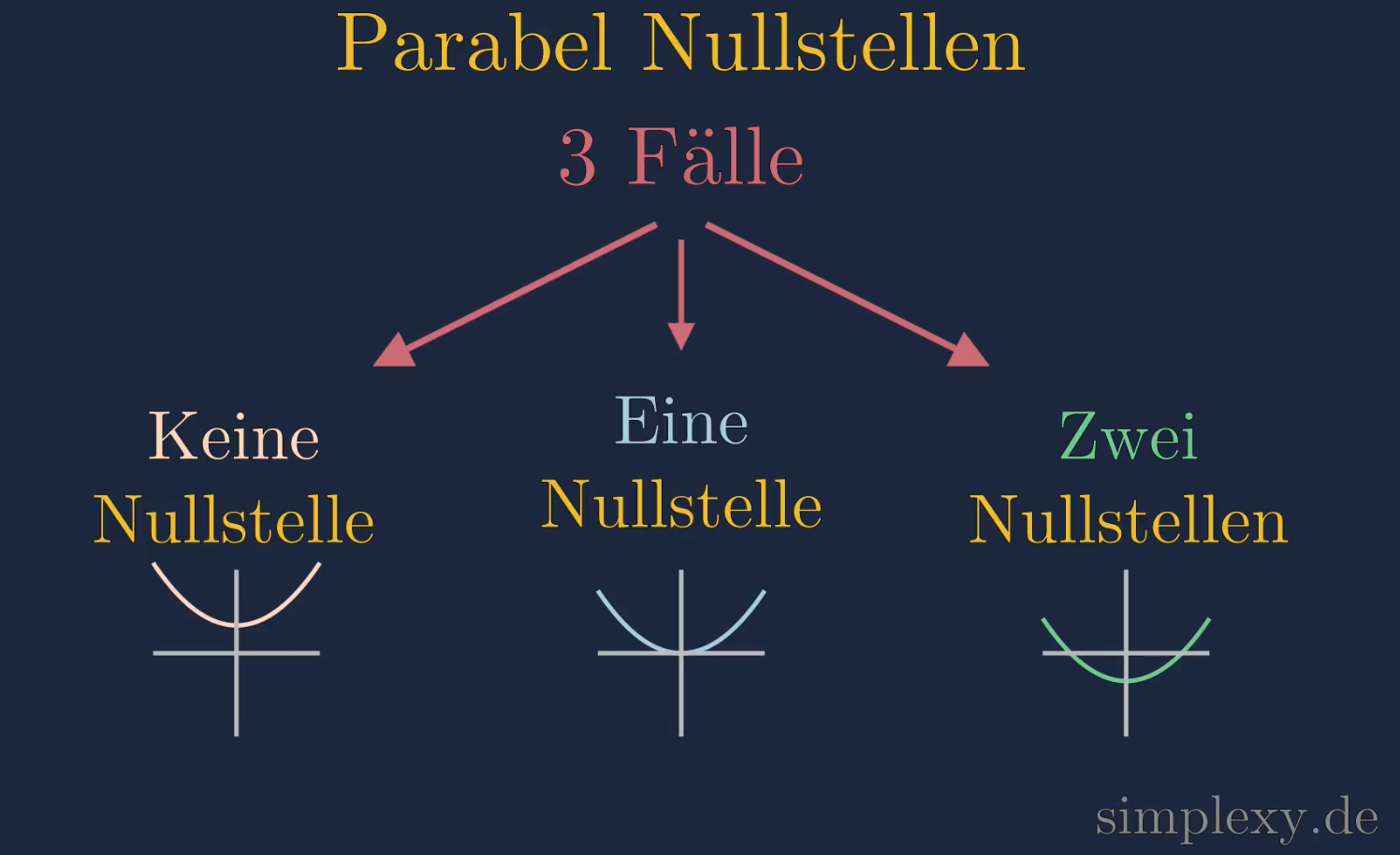
Es gibt verschiedene Methoden, um die Nullstellen einer Parabel zu berechnen. Die bekannteste ist die Mitternachtsformel (auch bekannt als quadratische Lösungsformel). Sie ist zwar etwas komplexer, funktioniert aber immer. Eine andere Möglichkeit ist die pq-Formel, die einfacher anzuwenden ist, wenn die Parabel in der Normalform (x² + px + q = 0) vorliegt. Und natürlich kann man manchmal die Nullstellen auch durch Faktorisierung finden, also durch das Zerlegen des quadratischen Terms in zwei lineare Faktoren. Welche Methode am besten geeignet ist, hängt von der jeweiligen Gleichung ab.
Wie fängt man nun am besten an? Such dir eine einfache Parabelgleichung aus, zum Beispiel y = x² - 4. Versuche, die Nullstellen mit der pq-Formel zu berechnen. Es gibt unzählige Online-Rechner und Tutorials, die dir dabei helfen können. Wichtig ist, nicht aufzugeben, wenn es beim ersten Mal nicht klappt. Mathematik ist wie ein Muskel, der trainiert werden muss. Und mit etwas Übung wirst du bald zum Parabel-Profi!
Das Schöne an der Beschäftigung mit Parabeln und ihren Nullstellen ist, dass es weit mehr ist als nur stumpfes Rechnen. Es ist eine Reise in die Welt der Muster und Formen, eine Entdeckung der Schönheit und Eleganz der Mathematik. Und wer weiß, vielleicht entdeckst du dabei ja auch deine eigene kreative Ader!