Wie Findet Man Die Höhe Eines Dreiecks Heraus

Okay, Leute, stellt euch vor: Ihr sitzt im Café, Cappuccino in der Hand, und eure Freunde streiten sich darüber, wie man die Höhe eines Dreiecks berechnet. Plötzlich schauen alle euch erwartungsvoll an. Keine Panik! Hier kommt eure Rettung, präsentiert mit einer Prise Humor und einer großen Portion "Ich hab's drauf!".

Was zur Hölle ist überhaupt eine Höhe?

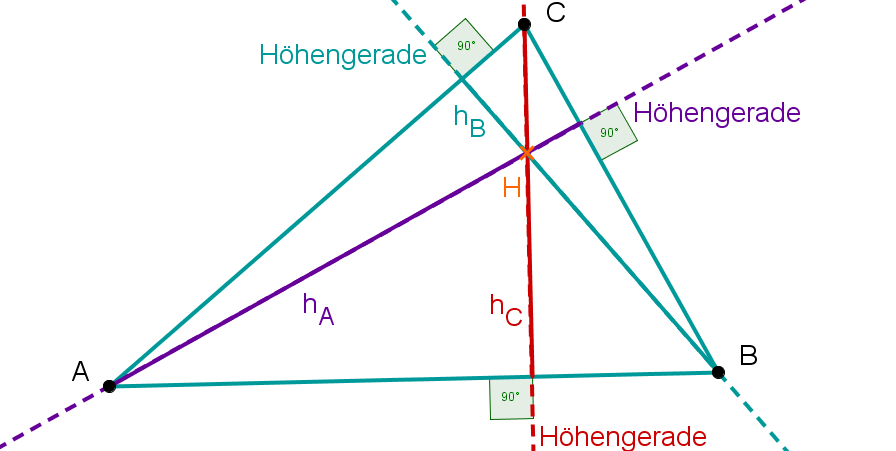
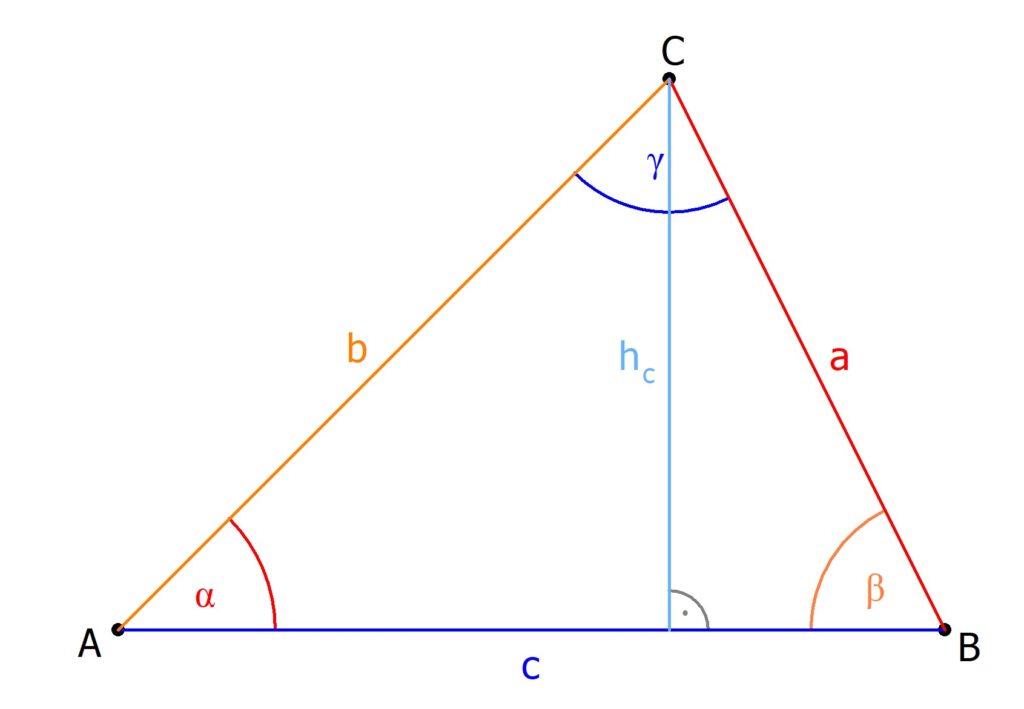
Die Höhe eines Dreiecks ist, im Grunde, wie ein Mini-Bergsteiger, der von der höchsten Spitze (dem Gipfel, sozusagen) senkrecht hinunter zur gegenüberliegenden Seite klettert (die wir dann als Basis bezeichnen). Wichtig: Er muss senkrecht klettern, sonst gibt’s Punktabzug! Stellt euch vor, er rutscht ab. Das zählt nicht!

Das Problem ist, dass Dreiecke kleine Betrüger sind. Sie können spitz (spitzwinklig), stumpf (stumpfwinklig) oder sogar rechtwinklig sein. Und jedes dieser kleinen Monster hat seine eigene Art, seine Höhe zu verstecken.

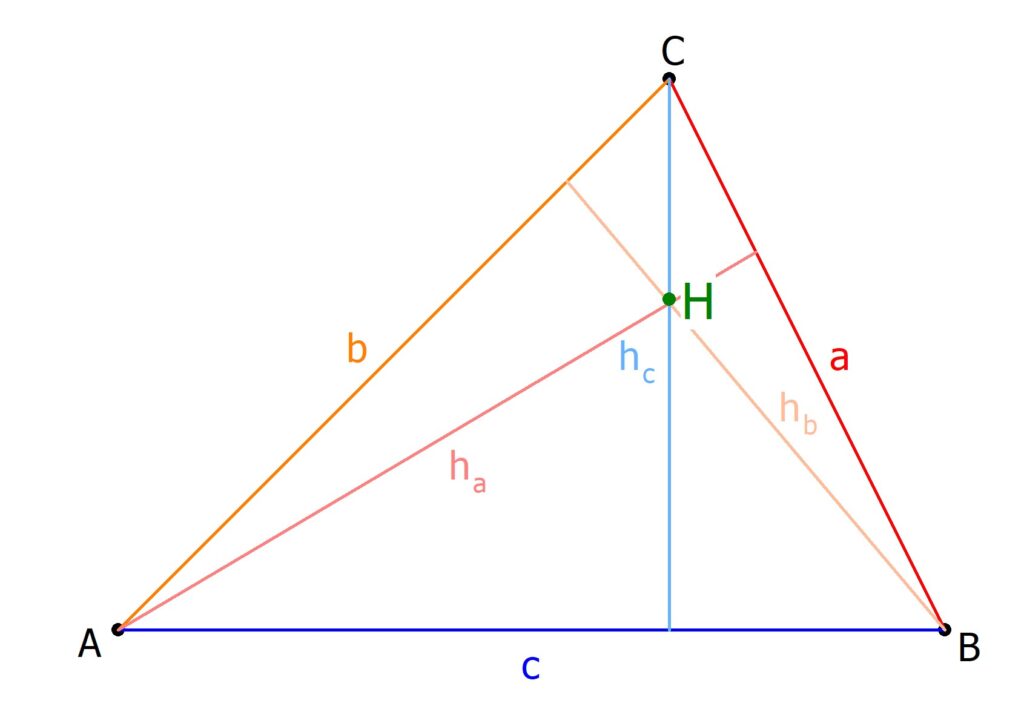
Die drei Musketiere der Höhenfindung:

Es gibt nicht *eine* Methode, sondern gleich mehrere! Je nach dem, was ihr bereits über das Dreieck wisst, könnt ihr die passende auswählen. Denkt an sie wie an Superhelden mit jeweils eigenen Spezialfähigkeiten:

1. Der Flächenheld: Wenn ihr die Fläche und die Länge einer Seite (Basis) kennt, ist das ein Kinderspiel.
2. Der Pythagoras-Pfleger: Für rechtwinklige Dreiecke und spezielle andere Fälle.
3. Der Trigonometrie-Titan: Wenn Winkel und Seiten ins Spiel kommen.

Methode 1: Der Flächenheld (Fläche und Basis sind eure Freunde)

Erinnert ihr euch noch an die Formel für die Fläche eines Dreiecks? Fläche = (1/2) * Basis * Höhe. Klingt kompliziert? Ist es nicht! Stellt euch vor, die Fläche ist der Geldbetrag, den ihr für den Garten (das Dreieck) bezahlt habt, und die Basis ist die Länge der Zaunlinie. Die Höhe ist dann der Preis pro Meter Zaun (fast so, als ob wir das Dreieck einzäunen wollen!).

Also, wenn ihr die Fläche (A) und die Basis (b) kennt, könnt ihr die Formel einfach umstellen: Höhe (h) = (2 * A) / b. BOOM! Problem gelöst. Ihr seid der Held der Stunde!

Beispiel: Die Fläche ist 20 cm² und die Basis ist 5 cm. Dann ist die Höhe (2 * 20) / 5 = 8 cm. Kinderleicht, oder?

Methode 2: Der Pythagoras-Pfleger (Achtung, nur für spezielle Fälle!)

Pythagoras, der alte Grieche, der Dreiecke genauso liebte wie wir. Sein berühmter Satz (a² + b² = c²) ist besonders nützlich bei rechtwinkligen Dreiecken. Aber auch bei anderen Dreiecken kann er helfen, wenn man ein bisschen trickst!

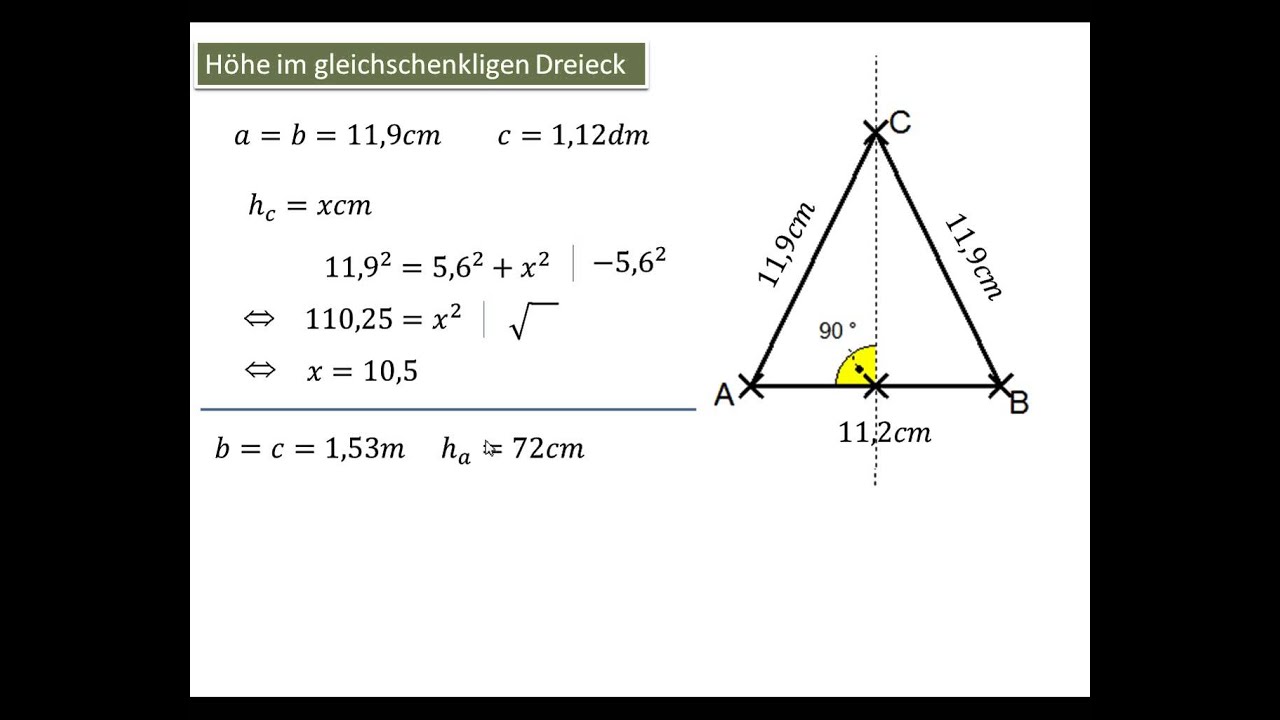
Stellt euch vor, ihr habt ein gleichschenkliges Dreieck (zwei Seiten sind gleich lang). Die Höhe teilt dieses Dreieck in zwei identische rechtwinklige Dreiecke. Jetzt könnt ihr Pythagoras anwenden, um die Höhe zu berechnen!

Beispiel: Ein gleichschenkliges Dreieck hat Seiten von 5 cm, 5 cm und 6 cm. Die Basis (6 cm) wird durch die Höhe halbiert (3 cm). Jetzt haben wir ein rechtwinkliges Dreieck mit Seiten von 3 cm, h (die Höhe) und 5 cm (Hypotenuse). Also: 3² + h² = 5². Daraus folgt: h² = 16, und h = 4 cm. Tadaaa!

Methode 3: Der Trigonometrie-Titan (Winkel und Seiten sind eure Waffen!)

Okay, jetzt wird es ein bisschen "fancy". Sinus, Kosinus und Tangens sind eure neuen besten Freunde. Keine Sorge, es ist nicht so schlimm, wie es klingt.

Wenn ihr einen Winkel (α) und die Länge einer Seite (a) kennt, die nicht die Basis ist (sondern eine der anderen Seiten!), dann könnt ihr die Formel Höhe (h) = a * sin(α) verwenden. Das 'sin(α)' holt ihr euch aus dem Taschenrechner (oder fragt Google).

Beispiel: Eine Seite ist 10 cm lang und der Winkel zwischen dieser Seite und der Basis ist 30 Grad. Dann ist die Höhe h = 10 * sin(30°). Da sin(30°) = 0.5, ist die Höhe h = 10 * 0.5 = 5 cm.

Die Sache mit den stumpfwinkligen Dreiecken...

Stumpfwinklige Dreiecke sind kleine Dramaqueens. Ihre Höhe liegt manchmal außerhalb des Dreiecks! Stellt euch vor, die Basis wird verlängert, und die Höhe fällt von der Spitze senkrecht auf diese Verlängerung. Keine Panik, die Methoden bleiben gleich, aber ihr müsst euch das vielleicht bildlich vorstellen.

Fazit: Ihr seid jetzt Dreiecks-Experten!

So, da habt ihr es. Egal, ob ihr die Fläche, rechtwinklige Verhältnisse oder trigonometrische Funktionen habt, ihr seid jetzt gewappnet, um jede Dreieckshöhe zu bezwingen. Geht raus und beeindruckt eure Freunde mit eurem neuen Wissen! Und denkt daran: Mathe kann auch Spaß machen (manchmal zumindest!). Jetzt aber zurück zum Cappuccino!